5.2. Расчет линейной электрической цепи постоянного тока методом узловых потенциалов

При расчете линейной электрической цепи методом узловых потенциалов, необходимо решить следующее матричное уравнение:

G_уφ_у = J_у,

где G_у – матрица узловых проводимостей; φ_у = (φ₁ φ₂ … φ_n) – матрица узловых потенциалов; J_у – матрица узловых токов.

Матрица узловых проводимостей составляется следующим образом:

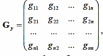
где g₁₁, g₂₂, g_nn – суммарные проводимости 1-го, 2-го и n-го узлов; g₂₁ = g₁₂ – проводимость ветви между первым и вторым узлами, взятая со знаком «–»; g_kn = g_nk – проводимость ветви между узлом n и узлом k, взятая со знаком «–» (если между узлами нет прямой связи, проводимость берется равной 0).

Матрица узловых токов определяется следующим образом:

J_у = (J_у1 J_у2 … J_уk)

где – суммарный ток первого узла; k – количество узлов в схеме; n – номер узла; i – номер входящей в узел ветви; m – количество ветвей, входящих в узел; Eni – ЭДС ветви, входящей в узел (берется со знаком «–», если ЭДС направлена от узла, и со знаком «+», если ЭДС направлена к узлу); g_ni – проводимость соответствующей ветви, входящей в узел.

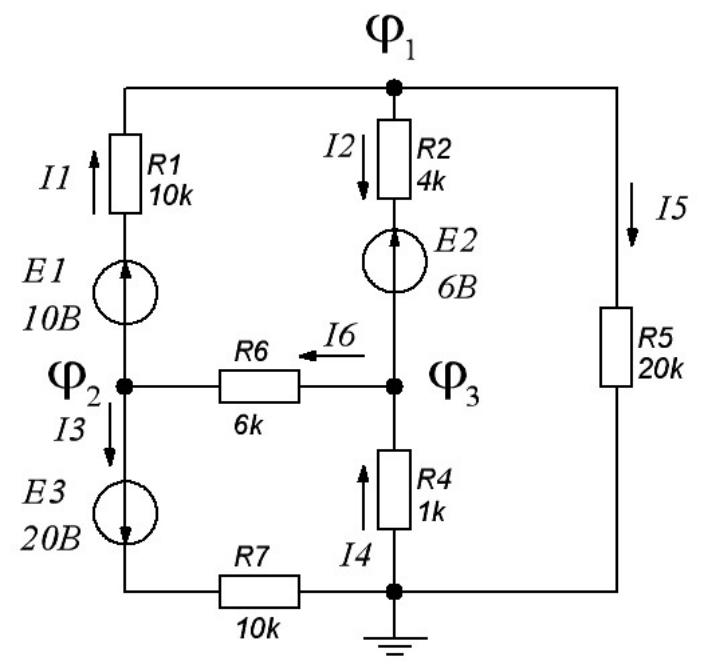
Рис 5.2

Для схемы на рис. 5.2 матрица узловых проводимостей будет иметь следующий вид:

g₁₁ = 1/R1 + 1/R2 + 1/R5 = 1/10 + 1/4 + 1/20 = 0,4 (мСм);

g₂₂ = 1/R1 + 1/R6 + 1/R7 = 1/10 + 1/6 + 1/10 = 0,367 (мСм);

g₃₃ = 1/R6 + 1/R2 + 1/R4 = 1/6 + 1/4 + 1/1 = 1,417 (мСм);

g₁₂ = g21 = -1/R1 = -1/10 = -0,1 (мСм);

g₁₃ = g31 = - 1/R2 = -1/4 = -0,25 (мСм);

g₂₃ = g32 = -1/R6 = -1/6 = -0,167 (мСм);

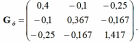
Матрица узловых токов для схемы на рис. 5.2 будет следующей:

J_у1 =I1-I2-I5= E1/R1 + E2/R2 = 10/10 + 6/4 = -0.5 (мА);

J_у2 =I6-I1-I3= -E1/R1 – E3/R7 = -10/10 – 20/10 = -3 (мА);

J_у3 = I2+I4-I6= E2/R2 = -6/4 = 1,5 (мА);

J_у = (J_у1 J_у2 J_у3)T = (-0,5 -3 1,5)

В результате получаем следующее матричное уравнение:

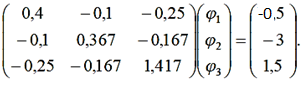
Решениями матричного уравнения являются значения потенциалов узлов схемы φ1, φ2, φ3. На основе известных потенциалов узлов можно рассчитать токи ветвей следующим образом:

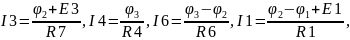
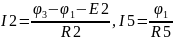
Рассмотрим пример модели в Mathcad

!!! в Mathcad элементы матрицы нумеруются с нулевого элемента, то есть, если у вас матрица М содержит 5 элементов, то они будуи иметь следующие номера: М₀, М₁, М₂, М₃, М₄

Метод контурных токов:

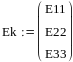
Для проверки вычислим баланс мощностей:

Метод узловых потенциалов:

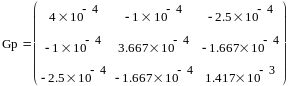
Для проверки вычислим баланс мощностей:

Задание на лабораторную работу:

1. Составить в MathCad математическую модель расчета электрической цепи согласно варианту.

2. Выполнить расчет по построеной модели.

Варианты заданий:

№		схема
1
2
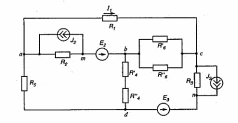
3
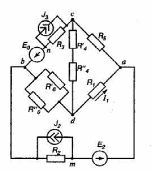
4
5
6
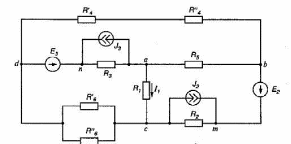
7
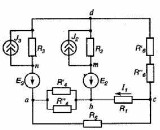
8
9
10
11
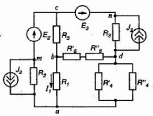
12
13
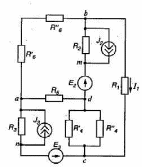
14
15
16
17
18
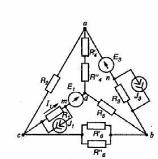
19
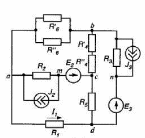
20
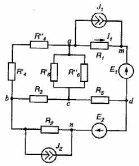
21
22

Номиналы элементов по вариантам

Номер варианта	R1	R2	R3	R4	R5	R6	R7	R8
	кОм	кОм	кОм	кОм	кОм	кОм	кОм	кОм
1	2	3	4	6	4	4	7	8
2	2	4	6	2	4	6	2	4
3	3	5	6	3	5	4	2	2
4	4	6	8	2	4	3	3	5
5	8	5	4	6	6	7	2	3
6	4	4	5	3	2	3	2	3
7	3	4	4	5	6	7	8	2
8	4	6	8	2	4	3	3	5
9	6	4	5	4	5	8	3	2
10	5	5	6	5	2	2	2	2
11	2	4	2	6	3	3	5	4
12	2	2	6	6	2	4	4	5
13	3	5	3	8	6	5	6	6
14	2	3	5	4	3	6	2	5
15	2	3	2	5	5	5	6	4
16	8	2	4	4	2	4	4	4
17	3	5	5	8	4	4	5	6
18	6	2		5	5	6		4
19	6	4	5	4	5	8	3	2
20	5	5	6	5	2	2	2	2
21	8	3	5	8	9	4	1	6
22	6	5	4	7	3	6	4	8

Номиналы резисторов, обозначенные на схеме штрихом или двумя штрихами брать из своей строки, но со следующим индексом, например, если у вас в схеме есть резисторы R1, R3, R4, R6, R’4, R”4, то берем R’4= R2 и R”4= R5.

№ варианта	E1, В	E2, В	E3, В	J1, А	J2, А
1	30	40	50	60	20
2	40	50	40	20	10
3	40	20	30	40	10
4	35	40	70	25	15
5	50	30	40	50	30
6	40	50	60	30	15
7	20	30	40	50	20
8	35	40	70	25	15
9	40	30	20	50	20
10	50	40	30	20	10
11	35	45	51	65	15
12	45	55	41	64	18
13	55	25	31	63	21
14	65	45	71	62	25
15	32	35	41	61	29
16	42	55	61	59	36
17	52	35	71	58	41
18	62	45	21	57	45
19	37	44	31	56	47
20	47	54	41	55	48
21	57	24	79	54	52
22	61	34	56	53	66

Контрольные вопросы

1. Описать алгоритм метода контурных токов

2. Описать алгоритм метода узловых потенциалов

3. Сравнить эти методы, в каком случае предпочтительнее использовать тот или другой метод

4. Как можно проверить правильность построения математической модели

5. Нарисовать блок-схему вычисления токов контура методом узловых потенциалов

6. Какие еще вы знаете методы нахождения токов контура, написать алгоритм вычисления