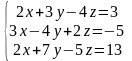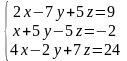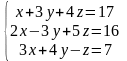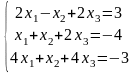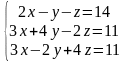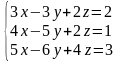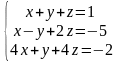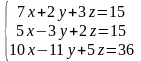Лабораторная работа 3 Решение слау. MathCad.

Теоретическое введение

В матричной форме СЛАУ записывается в эквивалентном виде:

,

Где — матрица коэффициентов СЛАУ размером n*n, 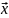— вектор неизвестных, 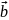, — вектор правых частей уравнений.

В Mathcad СЛАУ можно решить как в более наглядной форме, так и в более удобной для записи. Для первого способа следует использовать вычислительный Given/Find, а для второго — встроенную функцию Isolve, или метод обратной матрицы.

Isolve (A,b) — решение системы линейных уравнений, где: А — матрица коэффициентов системы; b – вектор правых частей.

Примеры:

1. Метод обратной матрицы

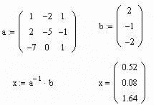
2. Функция Isolve

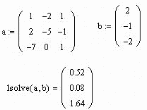
3. вычислительный метод Given/Find

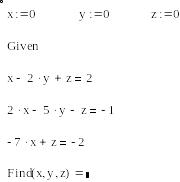
Задание на лабораторную работу:

Согласно варианту (табл. 3.1) найти решение СЛАУ тремя методами.

Таблица 3.1

вариант	СЛАУ	вариант	СЛАУ
1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20
21		22
23		24

Контрольные вопросы:

1. Что такое матрица?

2. Назовите основные виды матриц.

3. Приведите способы вычисления определителя матрицы.

4. Определение обратной матрицы.

5. Приведение матрицы к треугольному виду.

6. Определитель треугольной матрицы.

7. Суммирование матриц.

8. Умножение матриц.

9. Поиск определителя матрицы произвольного порядка методом разложения.

10. Дайте определение понятию минор матрицы.

11. Дайте определение понятию дополнительный минор матрицы.

12. Приведите формулу для нахождения алгебраического дополнения матрицы.

Лабораторная работа 4 Интерполяция вольт-амперных характеристик нелинейных элементов электрических цепей

Теоретическое введение

Интерполяция – метод аналитического описания зависимости величин по имеющемуся набору значений этих величин. Схожим по назначению является метод аппроксимации, однако отличием метода интерполяции от аппроксимации является полное совпадение вычисленной зависимости в узлах интерполяции.

Простейшим примером применения интерполяции является следующий: в дискретные моменты времени получены некоторые экспериментальные данные, необходимо по полученным данным определить зависимость измеренных величин (рис. 4.1).

Рис 4.1 пример интерполяции функции по 3 точкам

Основными методами интерполяции являются следующие:

1. Многочлен Лагранжа.

2. Интерполяционная формула Ньютона.

3. Линейная интерполяция.

4. Сплайны.

Во многих электротехнических задачах встречаются нелинейные зависимости, которые не позволяют выполнить аналитическое решение. В таких случаях прибегают к численным методам решения задач в совокупности с приближениями. Основные виды нелинейных зависимостей показаны на рис. 4.2

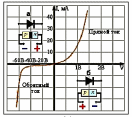
Рис. 4.2.(а) – ВАХ диода

Рис. 4.2.(б) – выходная и управляющая характеристики полевого транзистора

Рис. 4.2.(в) ВАХ тиристора

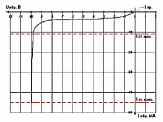
Рис 4.2 (г) обратная ВАХ диода

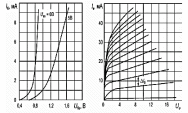
Рис 4.2 (д) ВАХ входная и выходная биполярного трпнзистора

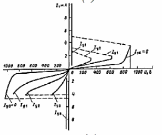
Рис 4.2 (е) ВАХ симистора

В данной лабораторной работе мы используем в расчетах полином Лагранжа.

Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях N<20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).

Полином Лагранжа находится в виде:

(4.1)

где базисные полиномы определяются по формуле:

(4.2)

 обладают следующими свойствами:

• являются многочленами степени n

• l_i(x_i)=1

• l_i(x_i)=0 при j≠i

Отсюда следует, что L(x), как линейная комбинация L_i(x), может иметь степень не больше n, и L(x_i)=y_i

Например:

1. В результате эксперимента получили следующие данные (табл. 4.1):

Аблица 4.1

Ik, mA	0,1	0,2	0,3	0,35	0,38	0,39
Uкэ, В	1	3	5	7	9	11

2. Вычислить напряжение коллектора при токе коллектора 0,25mA.

3. Заполняем таблицу 4.2 в соответствии с правилами заполнения полинома Лагранжа.

Таблица 4.2

x0	x1	x2	x3	x4	x5
0,1	0,2	0,3	0,35	0,38	0,39
f(x0)	f(x1)	f(x2)	f(x3)	f(x4)	f(x5)
1	3	5	7	9	11

4. Согласно алгоритму (формула 4.2) поэтапно вычисляем значения полинома при x=0.25

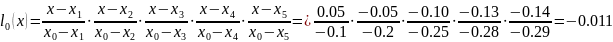
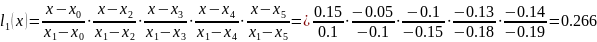
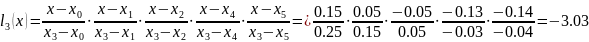
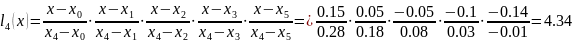
5. Вычисляем значение функции, формула 4.1

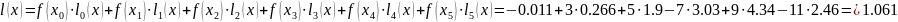
6. Или, используя те же формулы, можно получить функцию в аналитической форме:

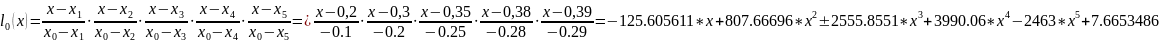
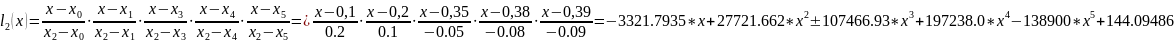
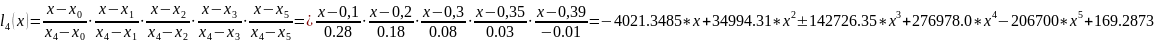
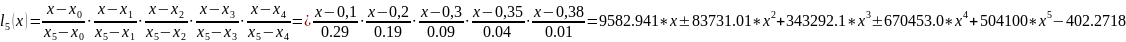
7. Подставляем в формулу 4.1, упрощаем с использованием функций MathCad, получаем:

f(x)=l₀(x)*f(x₀)+ l₁(x)*f(x₁)+ l₂(x)*f(x₂)+ l₃(x)*f(x₃)+ l₄(x)*f(x₄)+ l₅(x)*f(x₅)=

=119515.622119*x-1.04020483754e6*x²+4.2445551839e6*x³-8.24267134e6*x⁴+6157107*x⁵-5030.3729784

8. Программа:

Форма включает в себя компоненты: StringGrid, Edit, Lable, Button.

9. Код программы:

int n;

double lagx[1000];

double lagfx[1000];

//---------------------------------------------------------------------------

void __fastcall TForm1::Edit1Change(TObject *Sender)

{

StringGrid1->ColCount=StrToInt(Edit1->Text)+1;

//задаем количество столбцов в таблице

}

//---------------------------------------------------------------------------

void __fastcall TForm1::FormCreate(TObject *Sender)

{

StringGrid1->Cells[0][0]='x'; //название строки

StringGrid1->Cells[0][1]="f(x)";

}

//---------------------------------------------------------------------------

void __fastcall TForm1::Button1Click(TObject *Sender)

{

double x,s,s0;

n=StrToInt(Edit1->Text); //количество точек

x=StrToFloat(Edit2->Text); //расчетное значение

s=0;

for (int i=0;i<n;i++)

{

lagx[i]=StrToFloat(StringGrid1->Cells[i+1][0]);

lagfx[i]=StrToFloat(StringGrid1->Cells[i+1][1]);

}

//считывание значение из таблицы в массив "х" и "f(x)"

for (int i=0; i<n ;i++)

{

s0=1;

for (int j=0; j<n ;j++)

{

if (i!=j) s0=s0*(x-lagx[j])/(lagx[i]-lagx[j]);

//формирование l(x)

}

s=s+lagfx[i]*s0;//вычисление значения функции

}

Edit3->Text=FloatToStr(s);

}

Задание на лабораторную работу:

Согласно варианту (табл 4.3) написать программу в среде программирования «Borland C». Работа считается выполненной после проверки работоспособности программного кода.

Таблица 4.3

вариант			0		1		2		3		4		5		6		7		8
1	x	23		11		25.6		28		31.2		18.4		12.9		22.7		33
	f(x)	5.6		4.2		15.1		16.8		20.7		16.5		11.0		25		27
2	x	2,2		4,8		29		25		3,7		28.5		3,9		4,7		21
	f(x)	5,4		2,9		28		31		5,9		27		3,7		25		2,8
3	x	32		8,3		2,8		30		5,8		26		5,9		31		27
	f(x)	12		4,7		2,9		29		5,6		25		5,8		30		26
4	x	5,9		25		3,8		2,9		4,0		2,5		5,6		29		22
	f(x)	1,2		31		25		8,3		8,2		9,8		4,4		15		2,6
5	x	8,2		30		31		4,7		1,1		5,7		8,1		9,8		6,3
	f(x)	11		29		30		25		4,3		4		8,3		5,6		4,8
6	x	4,3		28		29		31		6,7		6		11		4		2,9
	f(x)	6,8		2,8		27		30		9,1		8		4,5		6		8,3
7	x	9,1		2,9		13		9,8		12		6,3		6,8		7		4,7
	f(x)	12		3,8		8		5,7		2,8		4,8		9,9		2		25
8	x	13		3,9		2		4		8,3		2,9		5,7		12		31
	f(x)	14		3,7		9		6		4,7		8,4		5		5,9		5,7
9	x	15		5,9		7		2,2		25		4,7		6		1,2		4
	f(x)	9,8		5,8		15		5,4		31		29		8		9,1		6
10	x	5,7		5,6		23		32		30		31		2		1,2		8
	f(x)	4		4,0		5.5		12		5,9		33		9		13		2,3
11	x	6		8,1		2,2		5,9		1,2		29		7		14		9
	f(x)	8		2,8		5,4		1,2		8,2		28		15		1,5		7
12	x	2		2,9		32		8,2		1,1		0,11		6,3		9,8		15
	f(x)	9		3,8		12		11		4,3		43		4,8		5,7		30
13	x	7		3,9		5,9		4,3		6,8		6,6		2,9		4		9,8
	f(x)	15		3,7		12		9,1		9,2		9,3		8,3		6		5,7
14	x	6,3		5,9		13		12		4,7		5,7		4,6		8		4
	f(x)	4,8		5,8		14		2,9		25		4,9		25		5,6		6
15	x	2,9		5,6		15		8,2		31		6		33		4,6		2,2
	f(x)	8,3		4,0		9,8		4,7		27		8,1		30		8,1		5,4
16	x	4,7		4,9		5,7		25		26		3,8		29		3,3		32
	f(x)	21		2,5		4		3,9		25		3,5		3,6		3,7		8,3
17	x	31		33		6		2,9		2,5		2,6		3,7		5,7		4,7
	f(x)	30		22		8		8,3		2,8		8,6		5,9		4		25
18	x	29		24		4		7		5,7		4,9		5,8		6		23
	f(x)	28		31		6		15		4,7		25		5,6		8		27
19	x	27		30		8		23		6		31		5,1		2		2,6
	f(x)	26		29		6,3		5.6		8,1		3,0		4,0		25		2,5
20	x	25		28		4,8		2,2		9,8		29		4,7		3,9		2,8
	f(x)	2,5		11		2,9		5,4		5,7		31		2,4		2,9		2,1
21	x	2,8		4,3		8,3		32		4		30		31		8,5		2,4
	f(x)	2,9		6,8		4,7		29		2,9		24		3,9		7		3,8
22	x	3,8		9,1		25		28		8,3		2,8		5,6		2,9		8
	f(x)	3,9		8,3		31		11		4,7		27		4,0		8,2		6,3
23	x	3,7		4,7		2,8		4,3		25		26		8,1		7		4,8
	f(x)	5,9		25		5,7		6,8		32		29		3,8		15		2,9
24	x	5,8		31		4		9,1		30		2,5		3,9		23		8,3
	f(x)	5,6		30		6		8,3		5,9		2,5		3,7		5.6		4,7
25	x	4,0		9,8		5,6		4,7		5,7		2,8		5,1		11		25
	f(x)	8,1		5,7		5,9		9,9		4,4		5,4		5,8		4,3		6,8

Контрольные вопросы:

1. Что такое интерполяция и для чего она применяется?

2. Основные методы интерполяции.

3. Что такое сплайн? Какие виды сплайнов вы знаете?

4. Основные виды нелинейностей, встречающиеся в электротехнических задачах.

5. Что такое интерполяционный многочлен Лагранжа?

6. Расскажите о выборе вида интерполяции в конкретных электротехнических задачах.

Лабораторная работа 5

Разработка приложения расчета линейной электрической цепи постоянного тока

Теоретическое введение

5.1. Расчет линейных электрических цепей постоянного тока методом контурных токов

Для расчета линейной электрической цепи постоянного тока используется два основных метода: метод контурных токов и метод узловых потенциалов.

Рассмотрим линейную электрическую цепь постоянного тока, состоящую из трех контуров (см. рис. 5.1, где E1..3 – источники ЭДС, I1..3 – токи ветвей электрической цепи, R1, R2, R4, R5, R6 – активные сопротивления ветвей электрической цепи). Для каждого контура данной электрической цепи можно определить контурный ток (II, III, IIII), протекающий по всем ветвям контура, контурную (суммарную) ЭДС, а также контурное (суммарное) сопротивление. Между контурами располагаются ветви электрической цепи, обладающие активным сопротивлением, являющимся общим для двух контуров.

Согласно методу контурных токов система уравнений, описывающая электрическую цепь, может быть представлена в виде следующего матричного уравнения:

R_KI_K = E_K,

где I_k=(I₁,I₂…I_n) - матрица контурных токов; R_K – матрица контурных сопротивлений; E_K – матрица контурных ЭДС.

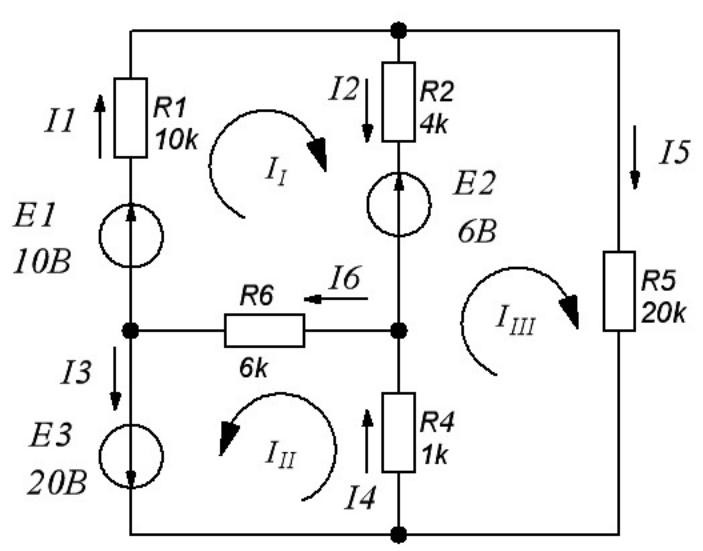
Рис. 5.1

Для пояснения принципа составления матрицы контурных сопротивлений, рассмотрим схему на рис. 5.1. В данном случае матрица R_K будет иметь следующий вид:

где R11, R22, R33 – суммарные контурные сопротивления соответствующих контуров; R12 = R21 – R13 = R31, R32 = R23 – смежные (общие) сопротивления 1-го и 2-го, 1-го и 3-го, а также 2-го и 3-го контуров, соответственно.

Знак перед смежными сопротивлениями в матрице RK определяется направлением контурных токов: если направление контурных токов в смежной ветви согласное, то знак «+», иначе – «–».

Рассчитаем сопротивления матрицы R_K для схемы на рис. 5.1:

R11 =R1+R2+R6= 20 (кОм) – суммарное сопротивление первого контура;

R22 = R4 + R6 = 7 (кОм) - суммарное сопротивление второго контура;

R33 = R2 + R4 + R5 = 25 (кОм) – суммарное сопротивление третьего контура;

R12 = R21 = R6 = 6 (кОм) – знак «+», потому что направление контурных токов I_I и I_II согласное;

R23 = R32 = R4 = 1 (кОм) – знак «+», потому что направление контурных токов I_II и I_III согласное;

R13 = R31 = -R2 = -4 (кОм) ) – знак «–», потому что направление контурных токов I_I и I_III противоположное.

Таким образом, матрица контурных сопротивлений для схемы на рис. 5.1:

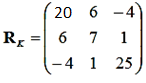
Матрица контурных ЭДС для схемы на рис. 5.1: E_K = (E_I , E_II , E_III), где E_I , E_II, E_III – контурные суммарные ЭДС.

Контурные ЭДС находятся следующим образом: производится обход ветвей соответствующего контура с суммированием ЭДС, сонаправленных с направлением контурного тока, и вычитанием ЭДС, направленных встречно контурному току.

Определим контурные ЭДС для схемы на рис. 5.1:

E_I = E1 – E2 = 10 – 6 = 4В; E_II = E3 = 20В; E_III = E2 = 6В; E_K = (4 20 6)

В итоге получаем матричное уравнение, описывающее состояние схемы на рис. 5.1, через контурные токи, контурные ЭДС и контурные сопротивления:

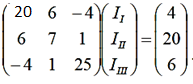
Данному матричному уравнению соответствует следующая система уравнений:

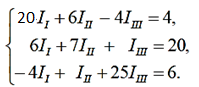
Токи ветвей электрической цепи находятся из контурных токов следующим способом. Если по ветви протекает только один контурный ток, то ток ветви по абсолютному значению равен контурному току. Знак тока ветви будет противоположным знаку контурного тока в случае их противоположной направленности, и знак тока ветви будет совпадать со знаком контурного тока в случае их согласной направленности.

Если по ветви протекает два контурных тока, то ток ветви будет равен сумме контурных токов, взятых со знаком «+». при согласном направлении с током ветви и со знаком «-». - при встречном направлении тока ветви.

Для рассматриваемой схемы токи ветвей можно определить из контурных токов следующим образом:

I1 = I_I, I2 = I_I – I_III, I3 = I_II, I4 = I_II + I_III, I5 = I_III, I6 = I_II + I_I.