3.3. Волновая оптика
3.3.1. Явление интерференции света
Волны, как и колебания, могут складываться. Сложение волн может быть интерференционным и неинтерференционным. Интерференцией называется сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны, не изменяющееся с течением времени. Интерференция наблюдается только от когерентных источников. Когерентность - значит согласованность. Когерентными источниками называются такие источники, которые дают волны одинаковой частоты, и для фиксированной точки пространства разность фаз колебаний остается постоянной.
Независимые источники света не могут быть когерентными, так как в каждом из них свет испускается множеством атомов, излучающих несогласованно. Разность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядочно меняется во времени. Когерентность можно обеспечить, разделив волну от одного источника на две части и затем сведя их вместе. Две части одной волны когерентны между собой и при наложении будут интерферировать.
Существуют различные методы получения когерентных световых источников. Самый простой из них - метод Юнга, в котором световая волна делится на две части с помощью экрана с двумя узкими параллельными щелями.
3.3.2. Условия максимума и минимума интенсивности при интерференции
Найдем условия максимума и минимума интенсивности при интерференции. Пусть S1 и S2 - два когерентных источника, совершающих колебания в одинаковой фазе. До точки наблюдения М волны проходят разное расстояние (рис. 3.8).
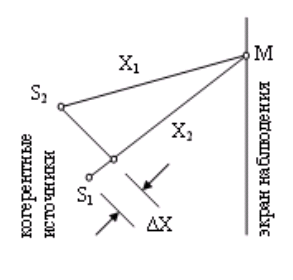
Рис.3.8
Запишем для них уравнения волн (3.24)
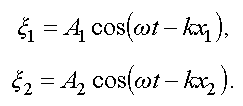
Найдем разность фаз складываемых волн
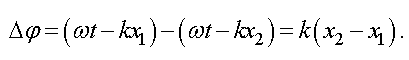
Обозначим через
Δx -
разность хода, т. е.
.
По формуле (3.22)
волновое число равно
,
тогда связь между разностью хода и
разностью фаз дается уравнением
Амплитуда результирующего колебания в точке наблюдения определяется уравнением (3.16)
.
Так как интенсивность пропорциональна
среднему значению квадрата амплитуды
(см. (3.34)):
,
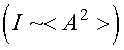то получим выражение для результирующей
интенсивности
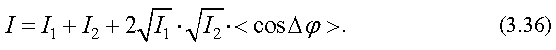
Если источники некогерентные, то
и
,
т. е. интерференция не наблюдается. Для
когерентных источников разность фаз
и
среднее значение косинуса равно косинусу
разности фаз
.
В тех точках пространства, где
интенсивность
,
а там, где
интенсивность
.
Следовательно, при наложении двух
когерентных световых волн происходит
пространственное перераспределение
световой энергии, в результате чего в
одних местах возникают максимумы, а в
других - минимумы интенсивности, т. е.
появляется интерференционная картина.
Максимумы интенсивности появляются
там, где
,
т. е. при
,
где m
= 0, 1, 2, ... Следовательно,
.
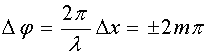Отсюда получим условие
максимума интенсивности при
интерференции
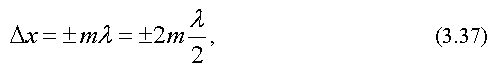
где m - порядок интерференционного максимума.
Условие максимума интенсивности при интерференции читается следующим образом.
Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.
Аналогично найдем условие минимума.
Если
,
то
,
где m
= 0, 1, 2, ...
Тогда
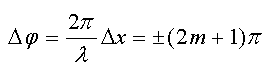
и
Условие минимума интенсивности при интерференции читается следующим образом.
Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.