2.17 Формулы Маклорена и Тейлора

В предыдущем параграфе был получен простейший вариант формулы Тейлора : . Эта формула приближенная, и она тем точнее, чем меньше . Но хотелось бы знать больше. Хотелось бы иметь оценку погрешности этой формулы. А еще лучше – иметь возможность заменить эту формулу на более точную, такую, чтобы ее погрешностью заведомо можно было бы пренебречь. С этой целью проведем в формуле переобозначения:

• старое обозначение x – новое обозначение x₀;

• старое обозначение – новое обозначение x;

• старое обозначение – новое обозначение .

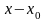Тогда эта формула примет вид:

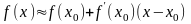(11)

То есть получаем приближенную формулу вида

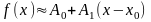, (12)

где 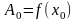; 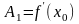. Использование этой приближенной формулы равносильно замене кривой на прямую с уравнением , которая является касательной, проведенной к графику функции в точке M₀ с абсциссой x₀ (рис. 1).

Действительно, прямая проходит через точку 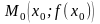. Кроме того, она имеет угловой коэффициент 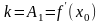. А это и есть, согласно геометрического смысла производной (см. 1.11), угловой коэффициент касательной, проведенной к графику функции в точке M₀. Для приближенная формула (12) становится точной. А для 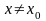она, очевидно, тем точнее, чем ближе x к x₀.

Д ля x, очень близких к x₀, замена кривой на касательную к ней, или как еще говорят, аппроксимация кривой её касательной, очевидно, вполне оправдана. Но с удалением x от x₀ расхождение между кривой и касательной к ней может стать существенным, а формула (12) может стать слишком грубой.

Возникает естественная мысль: поискать замену кривой не на прямую, а на другую кривую, только более простую (на параболу, гиперболу, и т.д.). В соответствии с этой мыслью приближенные значения функции для x, близких к x₀, будем искать по обобщению формулы (12):

(13)

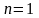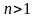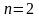В простейшем случае формула (13) совпадает формулой (12). А при мы вправе ожидать, что формула (13) окажется более точной, чем формула (12), и что ее точность будет возрастать с увеличением числа n. Действительно, аппроксимация кривой параболой (при ), кубической параболой (при 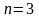) и т.д. более естественна, чем аппроксимация кривой какой угодной прямой. И чем сложнее аппроксимирующая кривая, тем качественнее может быть осуществлена эта аппроксимация. В том числе и для x, достаточно удаленных от x₀.

Потребуем, чтобы формула (13), как и ее частный случай (12), была точной при . Тогда получим:

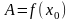(14)

Найдем остальные коэффициенты формулы (13). Предположим, что функцию можно сколько угодно раз дифференцировать в некоторой окрестности точки 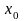, и продифференцируем обе части приближенного равенства (13) до n-го порядка включительно:

;

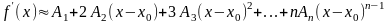; (15)

-------------------------------------------------------------------------

Здесь использовано обозначение:

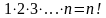(эн – факториал) (16)

В частности,

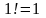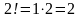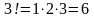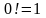; ; ; … (по определению) (17)

Приближенные равенства (15), как и исходное равенство (13), должны быть тем точнее, чем ближе x к x₀. Потребовав, чтобы при все они стали точными, получим:

; ; ; …

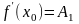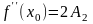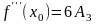Отсюда

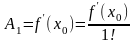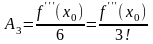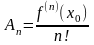; ; ; … (18)

Подставляя выражения (18) в (13), получим для x, близких к x₀:

(19)

Полученная ранее формула (11) является простейшим частным случаем этой формулы при .

Формула (19) – приближенная. Следует ожидать, что ее точность должна повышаться как при приближении x к x₀, так и при увеличении числа ее слагаемых n. Но чтобы убедиться в этом окончательно, следует получить оценку погрешности этой формулы для всех n, начиная с .

Обозначим символом 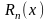эту погрешность ( – разность между левой и правой частями формулы (19)). Тогда получим точно для любых х и n:

(20)

Формула (20) называется формулой Тейлора. Последнее слагаемое называется остаточным членом формулы Тейлора. Поэтому еще говорят, что (20) – это формула Тейлора с остаточным членом.

При практическом использовании формулы Тейлора ее остаточный член отбрасывают, переходя тем самым к приближенной формуле (19), которую называют формулой Тейлора без остаточного члена. А для правомерности отбрасывания (игнорирования) остаточного члена используют его оценку, полученную французским математиком 19-го века Лагранжем:

(21)

Если – допустимая погрешность вычисления функции , то для данных x и x₀ подбирают такое значение n, чтобы .

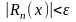При 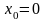формула Тейлора (20) принимает вид

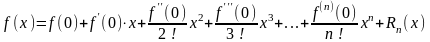(22)

и называется формулой Маклорена. Ее остаточный член оценивается по формуле (23), вытекающей из (21) при :

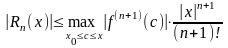(23)

Формулой Маклорена, после оценки и отбрасывания ее остаточного члена, пользуются для приближенного вычисления значений при x, близких к нулю.