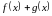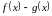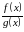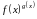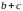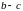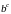- •1.2. Основные свойства переменных величин и их пределов
- •Если , и a и b конечны, то . То есть
- •1.13. Таблица эквивалентных бесконечно малых
- •2.3. Таблица производных основных элементарных функции
- •2.5. Дифференциал функции.
- •2.17 Формулы Маклорена и Тейлора
- •2.18, 2.19. Исследование функций с помощью производных
- •2.20 Асимптоты графиков функций
- •Нахождение вертикальных асимптот.
1.1 Если имеет место (2), то говорят, что переменная х стремится к числу а. Это число а называется пределом переменной x. И записывается это следующим образом:
<=>
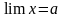 <=>
<=>
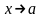 (3)
(3)
Читается: предел x равен a (x стремится к a).
Стремление переменной x к своему пределу a можно наглядно проиллюстрировать на числовой оси. Точный математический смысл этого стремления x к a состоит в том, что какое бы малое положительное число ни взять, а значит, каким бы малым промежутком ни окружить на числовой оси число a, в этот промежуток (в так называемую -окрестность числа a) попадут, начиная с некоторого номера N, все значения xn переменной x. В частности, на рис. 1 в изображенную -окрестность числа a попали все значения xn переменной x, начиная с номера .
Определение: Число а называется пределом последовательности ( пределом переменной х или пределом функции f(n)), если каково бы ни было наперед заданное положительное число , всегда можно найти такое натуральное число N, что для всех членов последовательности с номерами n>N будет выполняться неравенство .
1.2. Основные свойства переменных величин и их пределов
Если
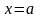 (переменная x
неизменна и равна постоянной a),
то естественно считать, что и
.
То есть предел постоянной равен ей
самой:
(переменная x
неизменна и равна постоянной a),
то естественно считать, что и
.
То есть предел постоянной равен ей
самой:
 (5)
(5)
Если ,
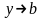 и a
и b
конечны, то
и a
и b
конечны, то
 .
То есть
.
То есть
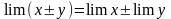 (6)
(6)
(предел суммы или разности переменных равен сумме или разности их пределов).
Если , и a и b конечны, то . То есть
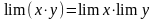 (7)
(7)
(предел произведения переменных равен произведению их пределов).
Если , , a и b конечны и
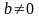 ,
то
,
то
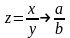 .
То есть
.
То есть
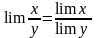 (8)
(8)
(предел частного равен частному пределов).
Если ,
 и
и
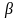 – любые постоянные числа, то
– любые постоянные числа, то
 .
То есть
.
То есть
 (9)
(9)
Действительно, на основании предыдущих свойств имеем:
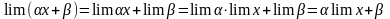 .
.
Если x – бесконечно малая переменная величина (
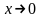 ),
то
),
то
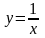 – бесконечно большая переменная
величина (
– бесконечно большая переменная
величина (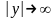 ).
).Если x – бесконечно большая переменная величина (
 ),
то
– бесконечно малая переменная величина
(
),
то
– бесконечно малая переменная величина
(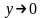 ).
).Если переменная x ограничена (это значит, что все ее значения xn расположены в некотором конечном числовом промежутке
 ),
а переменная y
бесконечно малая (
),
то переменная
),
а переменная y
бесконечно малая (
),
то переменная
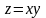 – тоже бесконечно малая (
– тоже бесконечно малая ( ).
).Если переменная x ограничена, а переменная y бесконечно большая ( ), то переменная
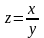 – бесконечно малая (
).
– бесконечно малая (
).Теорема Вейерштрасса.
а)
Пусть значения xn
переменной x
монотонно возрастают и при этом все они
меньше некоторой постоянной величины
C.
Такая переменная x
называется монотонно
возрастающей и ограниченной сверху
(числом C).
Она заведомо имеет конечный предел a,
причем
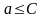 .
Наглядную иллюстрацию этой ситуации
дает рис. 2.
.
Наглядную иллюстрацию этой ситуации
дает рис. 2.

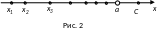
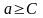 .
Наглядную иллюстрацию этой ситуации
дает рис. 3.
.
Наглядную иллюстрацию этой ситуации
дает рис. 3.
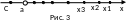
1.3. Пусть
даны множества действительных чисел
Х
и Y.
Функциональной
зависимостью ( функцией )
называется закон, по которому каждому
значению величины
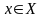 ,
называемой аргументом, ставится в
соответствие некоторое (единственное
) число
,
называемой аргументом, ставится в
соответствие некоторое (единственное
) число
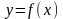 из множества Y.
Множество Х
называется областью
определения функции.
(D(f)).
Множество значений (E(f))
числовой функции f
называется множество всех
из множества Y.
Множество Х
называется областью
определения функции.
(D(f)).
Множество значений (E(f))
числовой функции f
называется множество всех
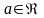 ,
для которых существует хотя бы одно
,
для которых существует хотя бы одно
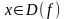 такое, что f(x)=a.В
математике словом «функция» называют
и закон (правило) соответствия f
и величину f(x).
такое, что f(x)=a.В
математике словом «функция» называют
и закон (правило) соответствия f
и величину f(x).
1.4. Существует три способа задания функцию:
Аналитический – задание функции формулой, показывающей способ вычисления значения функции по соответствующему значению аргумента. При аналитическом способе задания функция может быть задана явно, когда дано выражение у через х, т.е. формула имеет вид , неявно, когда x и y связаны между собой уравнением вида F(x,y)=0, а также параметрически, когда соответствующие друг другу значения x и y выражены через третью переменную величину t, называемую параметром.
Табличный – указание значений функции от соответствующих значений аргумента. Способ применяется в тех случаях, когда область определения функции состоит из конечного числа значений. В виде таблиц записывают результаты экспериментального исследования каких-либо процессов.
Графический . Для функции заданной графиком, по чертежу находятся приближенно значения y, отвечающие данным значениям х.
1.5. Вспомним основные функции, изученные в курсе элементарной математике и их графики.
линейная
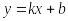 ,
D(f)=R,
E(f)=R
при
,
D(f)=R,
E(f)=R
при
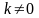 и {b}
при k
=0. Графиком является прямая с угловым
коэффициентом k,
который равен тангенсу угла наклона
прямой к оси абсцисс. Число b
– ордината точки пересечения графика
с осью ординат.
и {b}
при k
=0. Графиком является прямая с угловым
коэффициентом k,
который равен тангенсу угла наклона
прямой к оси абсцисс. Число b
– ордината точки пересечения графика
с осью ординат.

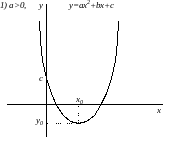
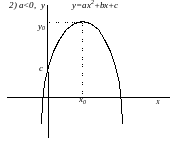
квадратичная
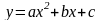 ,
D(f)=R,
E(f)=
,
D(f)=R,
E(f)=
 или
или
 .
Графиком является парабола.
.
Графиком является парабола.
обратно-пропорциональной зависимости
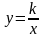 ,
D(f)=
,
D(f)=
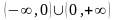 ,
E(f)=
.
Графиком является гипербола.
,
E(f)=
.
Графиком является гипербола.

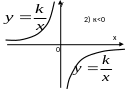
показательная
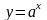 ,
D(f)=R,
E(f)=
,
D(f)=R,
E(f)=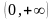 .
.
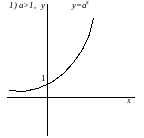
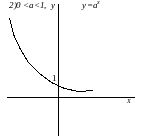
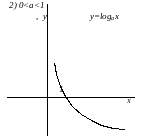
логарифмическая
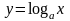 ,
D(f)=
,
E(f)=
R.
,
D(f)=
,
E(f)=
R.
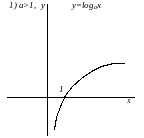
тригонометрические функции :
y=sinx,
D(f)=R,
E(f)=
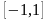 .
.
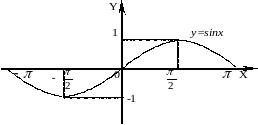
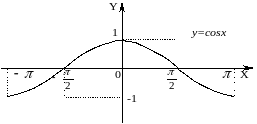
y=cosx, D(f)=R, E(f)= .
y=tgx,
D(f)= ,
E(f)=R.
,
E(f)=R.
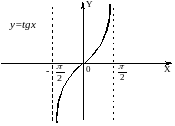
y=ctgx,
D(f)= ,
E(f)=R.
,
E(f)=R.

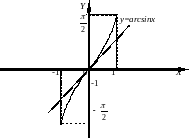
обратные тригонометрические функции :
y=arcsinx,
D(f)=
,
E(f)=
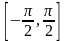 .
.
y=arccosx,
D(f)=
,
E(f)=
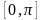 .
.

y=arctgx, D(f)=R, E(f)= .
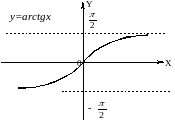
y=arcctgx, D(f)=R, E(f)= .
1.6. Пусть
– некоторая функция, рассматриваемая
на некотором числовом множестве оси ох
(например, на отрезке
 или на интервале
или на интервале
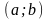 этой оси). И пусть x0
– некоторая внутренняя или граничная
точка этого множества. Для отрезка
такой точкой x0
может быть любая точка этого отрезка.
А для интервала
– любая точка этого интервала, включая
не принадлежащие ему его границы a
и b.
этой оси). И пусть x0
– некоторая внутренняя или граничная
точка этого множества. Для отрезка
такой точкой x0
может быть любая точка этого отрезка.
А для интервала
– любая точка этого интервала, включая
не принадлежащие ему его границы a
и b.
Будем
рассматривать значения функции
для аргумента x,
последовательно принимающего некоторые
значения (x1;
x2;
…xn;
…), выбранные таким образом, что
 .
При этом может оказаться, что соответствующая
последовательность значений (y1;
y2;
…yn;
…) функции
стремится к некоторому конечному или
бесконечному y0
(
.
При этом может оказаться, что соответствующая
последовательность значений (y1;
y2;
…yn;
…) функции
стремится к некоторому конечному или
бесконечному y0
( ).
И если это стремление y
к y0
осуществляется при
любом способе
стремления x
к x0,
то число y0
называется пределом
функции
при
.
И записывается это так:
).
И если это стремление y
к y0
осуществляется при
любом способе
стремления x
к x0,
то число y0
называется пределом
функции
при
.
И записывается это так:
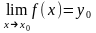 (1)
(1)
(читается:
предел функции
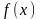 при
равен y0).
Обратно, равенство (1) означает, что при
функция
при
равен y0).
Обратно, равенство (1) означает, что при
функция
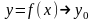 .
Причем стремление y
к y0
осуществляется при
любом способе
стремления x
к x0.
.
Причем стремление y
к y0
осуществляется при
любом способе
стремления x
к x0.
Дадим
формализованное определение предела
функцию Число А
называется пределом функции f(x)
при х,
стремящемся к a
( или в точке а
), если для любого наперед заданного
положительного числа
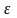 ( хотя бы и как угодно малого ) можно
найти такое положительное число
( хотя бы и как угодно малого ) можно
найти такое положительное число
 ,
что для всех значений х,
входящих в область определения функции,
отличных от а
и удовлетворяющих условию
,
что для всех значений х,
входящих в область определения функции,
отличных от а
и удовлетворяющих условию
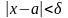 ,
имеет место неравенство
,
имеет место неравенство
 .
.
В
определении предела функции вовсе не
требуется, чтобы функция f(x)
была непременно определена в точке а.
Для того чтобы функция f(x)
имела возможность стремиться к пределу
при
 ,
необходимо лишь, чтобы в области её
существования были точки, как угодно
близкие к а
и отличные от а.
,
необходимо лишь, чтобы в области её
существования были точки, как угодно
близкие к а
и отличные от а.
1.7. Среди
функций, имеющих предел в точке, выделяют
бесконечно
малые и бесконечно большие функции.
Функция f(x)
называется
бесконечно малой
при
или
 ,
если
,
если или
или
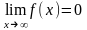 .
Функция f(x)
называется
бесконечно большой
при
,
если имеет место одно из равенств
.
Функция f(x)
называется
бесконечно большой
при
,
если имеет место одно из равенств
 ,
,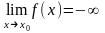 ,
,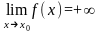 .(Аналогично
при
)
.(Аналогично
при
)
Для сравнения бесконечно малых функций обычно рассматривают их отношения.
Если
отношение
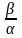 имеет конечный и отличный от нуля предел,
т.е. если
имеет конечный и отличный от нуля предел,
т.е. если
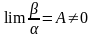 ,
а следовательно,
,
а следовательно,
 ,
то бесконечно малые
и
называются бесконечно
малыми одного порядка.
,
то бесконечно малые
и
называются бесконечно
малыми одного порядка.
Если
отношение двух бесконечно малых
стремится к нулю, т.е.
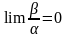 ( а
( а
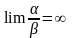 ), то бесконечно малая
называется бесконечно
малой величиной высшего порядка, чем
бесконечно малая
,
а бесконечно малая
называются бесконечно
малой низшего порядка, чем бесконечно
малая
.
), то бесконечно малая
называется бесконечно
малой величиной высшего порядка, чем
бесконечно малая
,
а бесконечно малая
называются бесконечно
малой низшего порядка, чем бесконечно
малая
.
1.8. При нахождении предела таких функций пользуются свойствами пределов функций. Сформулируем их.
1) Предел постоянной равен самой постоянной.
2) Постоянный множитель можно выносить за знак предела.
3)
Пусть функции
 имеют в точке
имеют в точке
 конечные пределы, соответственно равные
конечные пределы, соответственно равные
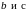 .
Тогда функции
.
Тогда функции
имеют в точке пределы, соответственно равные
Докажем некоторые из этих свойств из пункта 3.
Теорема 1. Предел алгебраической суммы двух функций равен алгебраической сумме пределов этих функций.
Доказательство:
пусть
lim
f(x)=b
и limg(x)=c,
тогда на основании первого свойства
бесконечно малых функций можем написать:
f(x)=b+
,
g(x)=c+
,
где
и
- бесконечно
малые функции. Значит f(x)+g(x)=
(b+c)
+(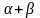 ),
т.к. (b+c)
– есть постоянная величина, а (
)
– величина бесконечно малая, тогда на
основании того первого свойства
бесконечно малых функций заключаем,
что lim(
f(x)+g(x))=b+c=
lim
f(x)+lim
g(x)
, что и требовалось доказать.
),
т.к. (b+c)
– есть постоянная величина, а (
)
– величина бесконечно малая, тогда на
основании того первого свойства
бесконечно малых функций заключаем,
что lim(
f(x)+g(x))=b+c=
lim
f(x)+lim
g(x)
, что и требовалось доказать.
Теорема 2. Предел произведения двух функций равен произведению пределов этих функций.
Доказательство:
пусть
lim
f(x)=b
и limg(x)=c,
тогда на основании первого свойства
бесконечно малых функций можем написать:
f(x)=
b+
,
g(x)=
c+
,
где
и
- бесконечно
малые функции. Значит f(x)*g(x)=
 .
Произведение bc
– есть величина постоянная, а
.
Произведение bc
– есть величина постоянная, а
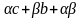 - бесконечно малая, на основании свойств
бесконечно малых функций. Таким образом,
по свойству 1 бесконечно малых функций
получаем что lim(
f(x)*g(x))=b*c=
lim
f(x)*lim
g(x),
что и требовалось доказать.
- бесконечно малая, на основании свойств
бесконечно малых функций. Таким образом,
по свойству 1 бесконечно малых функций
получаем что lim(
f(x)*g(x))=b*c=
lim
f(x)*lim
g(x),
что и требовалось доказать.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля.
Доказательство:
пусть
lim
f(x)=b
и limg(x)=c,
тогда на основании первого свойства
бесконечно малых функций можем написать:
f(x)=
b+
,
g(x)=
c+
,
где
и
- бесконечно
малые функции. Произведем следующие
преобразования:
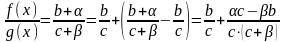 .
Дробь
.
Дробь
 есть постоянное число, а дробь
есть постоянное число, а дробь
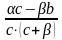 - бесконечно малая, на основании свойств
бесконечно малых функций. Таким образом,
по свойству 1 бесконечно малых функций
получаем что lim(
f(x)/g(x))=b/c=
lim
f(x)/lim
g(x),
что и требовалось доказать.
- бесконечно малая, на основании свойств
бесконечно малых функций. Таким образом,
по свойству 1 бесконечно малых функций
получаем что lim(
f(x)/g(x))=b/c=
lim
f(x)/lim
g(x),
что и требовалось доказать.
В
тех случаях, когда либо
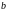 ,
либо
,
либо
 ,
либо оба вместе равны
,
либо оба вместе равны
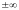 ,
или в частном
,
или в частном
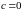 ,
применение указанных правил не дает
возможности найти предел составной
функции. Рассмотрим пример. Пусть
,
применение указанных правил не дает
возможности найти предел составной
функции. Рассмотрим пример. Пусть

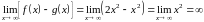 .
.
Возьмем теперь

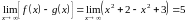 .
.
1.9. Рассмотрим и такой вид функций:
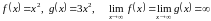 ,
,
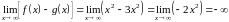 .
.
Такие ситуации, где значение предела зависит от конкретного вида функций участвующих в выражении, называются неопределенностями.
Предел
разности двух стремящихся к
 функций, значение которого зависит от
конкретного вида функций, называется
неопределенностью
вида
функций, значение которого зависит от
конкретного вида функций, называется
неопределенностью
вида
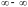 .
.
Предел
частного двух функций, стремящихся к
нулю, значение которого зависит от
конкретного вида функций, называется
неопределенностью
вида
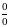 .
.
Аналогично
определяются и другие неопределенности: .
.
1.10. Об основных способах раскрытия неопределенностей уже мы говорили в предыдущей лекции. В этой лекции мы обсудим этот вопрос более подробно.
При
нахождении пределов функций вначале
необходимо вместо независимой переменной
 подставить ее предельное значение. Если
при этом получается конечное значение
функции, то оно и будет ее пределом. Если
при подстановке выясняется, что возникает
неопределенность, то нужно от нее
избавиться
раскрыть неопределенность. Для этого
раскрытия используются, в первую очередь,
два подхода. Первый: преобразование
функций,
стоящих под знаком предела, с помощью
алгебраических и тригонометрических
формул. Второй: выделение
в рассматриваемой функции некоторых
эталонных
пределов,
называемых замечательными. При раскрытии
неопределенностей после каждого
преобразования функции в нее подставляют
предельное значение переменной, чтобы
проверить, осталась ли неопределенность.
Действия продолжают до тех пор, пока
неопределенность не будет устранена.
подставить ее предельное значение. Если
при этом получается конечное значение
функции, то оно и будет ее пределом. Если
при подстановке выясняется, что возникает
неопределенность, то нужно от нее
избавиться
раскрыть неопределенность. Для этого
раскрытия используются, в первую очередь,
два подхода. Первый: преобразование
функций,
стоящих под знаком предела, с помощью
алгебраических и тригонометрических
формул. Второй: выделение
в рассматриваемой функции некоторых
эталонных
пределов,
называемых замечательными. При раскрытии
неопределенностей после каждого
преобразования функции в нее подставляют
предельное значение переменной, чтобы
проверить, осталась ли неопределенность.
Действия продолжают до тех пор, пока
неопределенность не будет устранена.
Предел
дробно-рациональной функции. Прежде
чем мы перейдем к разбору возможных
преобразований при возникновении
неопределенностей отметим еще раз тот
факт, что в области непрерывности любой
функции её предел равен значению функции
в указанной предельной точке, т.е. при
отыскании предела дробно-рациональной
функции можно в аналитическом выражении
функции заменить аргумент его предельным
значением, если при этом предельном
значении знаменатель не обращается в
нуль. Если
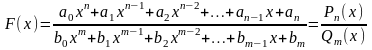 ,
то
,
то
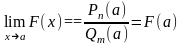 ,
при
,
при
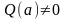 .
.
Пример
1: Найти
 .
.
Функция
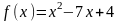 - целая рациональная. Заменим в
аналитическом выражении функции х
его предельным значением и получим:
- целая рациональная. Заменим в
аналитическом выражении функции х
его предельным значением и получим:
 .
.
Пример
2: Найти
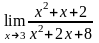 .
.
Функция
 - дробно-рациональная. Прежде чем заменять
в аналитическом выражении функции х
его предельным значением, нужно проверить,
не обращается ли в нуль знаменатель
дроби при х=3.
Проверяем:
- дробно-рациональная. Прежде чем заменять
в аналитическом выражении функции х
его предельным значением, нужно проверить,
не обращается ли в нуль знаменатель
дроби при х=3.
Проверяем:
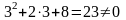 .
.
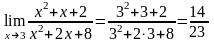
1.11. Вычислению многих пределов, содержащих неопределенности, часто помогает использование двух так называемых замечательных пределов:
1)
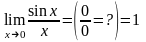 (x
– угол в радианах)
(x
– угол в радианах)
Докажем первый замечательный предел. Для этого вспомним школьную формулу для длины l произвольной дуги окружности (рис.1):
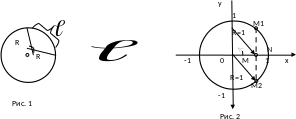
А теперь рассмотрим рис. 2:
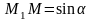 ;
;
 ;
;
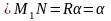 ;
;
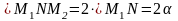 ;
;
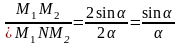 (
– в радианах).
(
– в радианах).
При
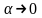 хорда M1M2
и дуга M1NM2,
неограниченно уменьшаясь, практически
становятся неразличимыми (малая дуга
практически не отличается от стягивающей
ее хорды). То есть их отношение стремится
к единице. Таким образом, при
дробь
хорда M1M2
и дуга M1NM2,
неограниченно уменьшаясь, практически
становятся неразличимыми (малая дуга
практически не отличается от стягивающей
ее хорды). То есть их отношение стремится
к единице. Таким образом, при
дробь
 .
А это и означает, что
.
А это и означает, что
 (
– угол в радианах)
(
– угол в радианах)
Полученный результат совпадает (при другом обозначении) с первым замечательным пределом (1).
1.12. 2)
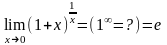 ,
где
,
где
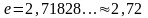 .
.
(
в другом виде
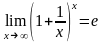 )
)
Второй замечательный предел, приводит к важному для всей высшей математики числу e (к Неперову числу – по имени шотландского математика 16–го века Джона Непера, введшего в математику это число). Приведем доказательство.
Теорема
1:
Переменная величина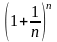 ,
где n-
натуральное число, при
,
где n-
натуральное число, при
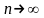 имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Доказательство: По формуле бинома Ньютона мы можем написать :
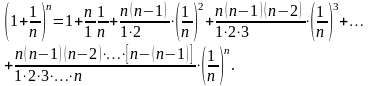
Произведем алгебраические преобразования.
 (2)
(2)
Из полученного равенства можно сделать вывод, что переменная величина является возрастающей. Действительно,
1) все члены разложения – положительны;
2)
при переходе от значения n
к (n+1)
каждое слагаемое суммы возрастает,
т.к.
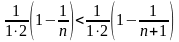 ;
;
3) добавляется ещё одно слагаемое.
Также
переменная величина
ограничена.
Докажем этот факт. Учитывая, что
 ;
;
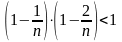 и т.д., из (2) получаем
и т.д., из (2) получаем
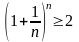 и
и
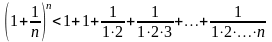 .
.
Заметив,
что
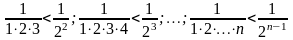 .
Используем эти оценки и получим:
.
Используем эти оценки и получим:
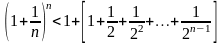 .
Слагаемые в квадратных скобках образуют
геометрическую прогрессию со знаменателем
.
Слагаемые в квадратных скобках образуют
геометрическую прогрессию со знаменателем
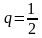 и первым членом
и первым членом
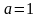 .
Поэтому
.
Поэтому
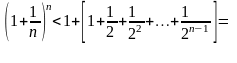
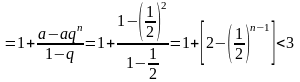 .
Подытоживая все сказанное, получаем :
.
Подытоживая все сказанное, получаем :
 .
.
Итак, переменная величина - возрастающая и ограниченная. На основании свойств пределов она имеет предел. Этот предел обозначим буквой е.