§3. Матриці.

Питання для самоперевірки:

1. Матрицею називається…

2. Транспонування матрицi – це…

3. Яка матриця називається симметричною…, ортогональною…, скалярною…, одиничною… .

4. Для яких матриць iснують одностороннi нейтральнi елементи? Навести приклад.

5. Умова існування добутку матриць…

6. Якi матрицi називаються комутативними? Чи завжди АВ = ВА?

Навести приклади комутативних матриць.

6. Умови виконання додавання i множення матриць одночасно…

7. Матриця А називається оберненою до матрицi А, якщо…

8. Необхiдна умова iснування оберненої матрицi…

9. Чи спiвпадають рядковий i стовпчиковий ранги матриць?

10. Елементарнимим перетвореннями матрицi є…

11. Розв’язати матричнi рiвняння:

a) XA = B; b) AX = B; c) AXB = C.

6. Чи є матриця А розв’язком рiвняння…

X = A=

14. Довести, що коли АВ = ВА, то А^-1B = BA^-1

Задачі:

1. Обчислити матрицю АВ, якщо

а)

b)

c)

2. Знайти обернену матрицю А^-1 для матриці А

3. Розв’язати матричне рівняння:

4. Довести, що коли АВ = ВА, то

а) А² - В² = (А + В)(А - В)

b) (A + B)² = A² + 2AB + B²

5. Знайти всі матриці другого порядку, квадрати яких дорівнюють одиничній матриці.

6. Знайти f(А), якщо

а) f(x) = x² - 3x + 2

b) f(x) =

c) f(x) =

7. Довести, що

8. Чи утворює множина матриць виду над полем R групу відносно операції множення матриць?

9. Чи утворює поле множина всіх матриць виду над полем R?

10. Довести, що матриця задовольняє рівняння х² - (a + d)x + ad - bc = 0

11. Розв’язати систему матричним методом

§4. Детермiнанти.

Питання для самоперевірки:

1. Записати правило “трикутника” для обчислення детермiнанта третього порядку…

2. Мiнор – це…

3. Алгебраїчне доповнення елемента – це…

4. Зв’язок мiж М_ij i А_ij…

5. В якому випадку детермiнант квадратної матрицi дорiвнює нулю?

6. Детермiнант n-го порядку – це…

7. Властивостi детермiнанта n-го порядку…

8. Правило Крамера…

9. Якщо при розв’язуванні СЛР методом Крамера детермiнант головної матрицi дорiвнює нулю і

1. всі _і = 0, то…

2.  _і  0, то…

10. Рангом матрицi називається …

11. Теорема про ранг матрицi…

12. Необхiдна i достатня умова iснування оберненої матрицi…

13. Пояснити як за допомогою детермiнанта можна знайти матрицю обернену до даної…

14. Якi з добуткiв належать детермiнанту i якого порядку:

1. а₂₁a₃₃a₅₅a₄₂a₁₄;

2. a₃₄a₂₅a₁₃a₂₂a₅₅. Вiдповiдь пояснити

15. Якщо в детермiнантi iснує рядок або стовпчик, всi елементи якого дорiвнюють нулю, крiм а_ij, то…

16. Розкласти детермiнант за елементами i-го рядка або j-го стовпчика означає…

17. Сума всiх попарних добуткiв елементiв довiльного рядка на алгебраїчнi доповнення елементiв другого рядка дорoвнює…

Задачі:

1. Обчислити детермінант, де і =

2. Розв’язати систему лінійних рівнянь методом Крамера

3. Не розкриваючи детермінанта довести, що

4. Розкласти за елементами n-го рядка і обчислити детермінант

5. Обчислити детермінант

6. Обчислити детермінант

7. Розв’язати рівняння

8. Обчислити обернену матрицю за допомогою алгебраїчних доповнень

9. Дослідити на визначеність систему і знайти її загальний розв’язок

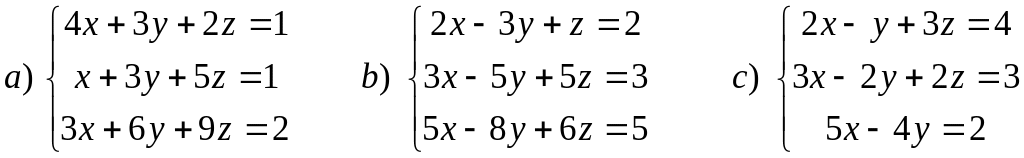
10. Обчислити ранг матриці методом окантування мінорів