Вопрос №7 Решение систем линейных уравнений с помощью обратной матрицы Обратная матрица

На множестве матриц не определена операция деления, она заменена умножением на обратную матрицу.

Определение

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

Квадратная матрица   называется обратной к невырожденной матрице   , если  , где   - это единичная матрица соответствующего порядка.

Замечание

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

Свойства обратной матрицы:

1°    

2°    

3°    

4°    

Нахождение обратной матрицы

Обратную матрицу можно найти с помощью двух ниже описанных методов.

Нахождение обратной матрицы с помощью присоединённой матрицы

Теорема

Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощьюэлементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

Пример

Задание. Для матрицы   найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице   справа единичную матрицу второго порядка:

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что 

Ответ. 

Замечание

Если на некотором этапе в "левой" матрице получается нулевая строка, то это означает, что исходная матрица обратной не имеет.

Облегченный способ для матрицы второго порядка

Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:

Шаг 1. Находим определитель   заданной матрицы, если он равен нулю, то делаем вывод, что обратной матрицы не существует, иначе переходим к следующему шагу.

Шаг 2. Элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный.

Шаг 3. Делим все элементы на   и получаем обратную матрицу.

Пример

Задание. Найти обратную матрицу для 

Решение. Шаг 1.   , тогда обратной матрицы не существует.

Ответ. Так как определитель матрицы   равен нулю, то она не имеет обратной.

Пример

Задание. Найти обратную матрицу для 

Решение. Шаг 1. Находим определитель: 

Шаг 2. 

Шаг 3. 

Ответ. 

Нахождение обратной матрицы с помощью союзной матрицы

Определение

Матрица   называется союзной к квадратной матрице   , если элементы матрицы   равныалгебраическим дополнениям соответствующих элементов матрицы   .

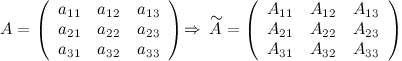
Имеет место следующее свойство: 

Тогда, если   , то   , а тогда 

Таким образом, матрица имеет союзную тогда и только тогда, когда она невырожденная.

Пример

Задание. Найти обратную матрицу к матрице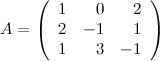 

Решение. Вычисляем определитель матрицы:

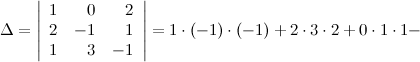
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица   к матрице  находится по формуле:

Найдем союзную матрицу   , для этого вычислим алгебраические дополнения к элементам матрицы   :

Таким образом,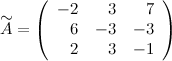 

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

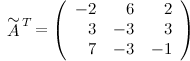
Итак, 

Ответ.