Свойства сложения матриц:

1.   Ассоциативность 

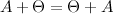2.    , где 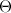  - нулевая матрица соответствующего размера.

3.   Коммутативность 

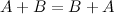
2.3 Умножение матрицы на число

Определение

Произведением матрицы   на ненулевое число   называется матрица   того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть  .

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Данная операция, вместе с операцией сложения матриц, относится к линейным операциям над матрицами.

Пример

Задание. Чему равна матрица  , если матрица   ?

Решение. 

Ответ. 

Свойства умножения матрицы на число:

1.   

2.   

3.   

4.   

5.   

2.4 Произведение матриц

определение

Произведением матрицы   на матрицу   называется матрица   такая, что элемент матрицы  , стоящий в  -ой строке и  -ом столбце, т.е. элемент  , равен сумме произведений элементов  -ой строки матрицы   на соответствующие элементы  -ого столбца матрицы  .

Замечание

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Пример

Задание. Вычислить   и  , если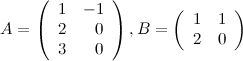 

Решение. Так как   , а   , то произведение возможно и результатом операции умножения будет матрица   , а это матрица вида   .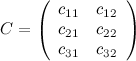

Вычислим элементы матрицы   :

Итак,   .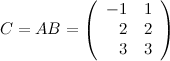

Выполним произведения в более компактном виде:

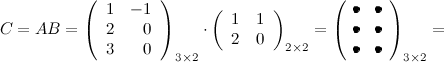
Найдем теперь произведение  . Так как количество столбцов матрицы  (первый сомножитель) не совпадает с количеством строк матрицы   (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. 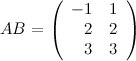  . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы   не совпадает с количеством строк матрицы   .

Свойства произведения матриц:

1. Ассоциативность 

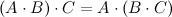
2. Ассоциативность по умножению 

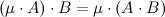
3. Дистрибутивность  , 

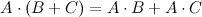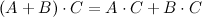
4. Умножение на единичную матрицу 

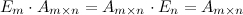
5. В общем случае умножение матриц не коммутативно, т.е. 

6. 

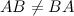
Вопрос №3 Обратная матрица, алгоритм ее вычисления.

3.1Определение.

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

Квадратная матрица   называется обратной к невырожденной матрице   , если  , где   - это единичная матрица соответствующего порядка.

Замечание.

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

Свойства обратной матрицы:

1°    

2°    

3°    

4°    

3.2 Нахождение обратной матрицы

Обратную матрицу можно найти с помощью двух ниже описанных методов.

Теорема

Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.

Пример

Задание. Для матрицы   найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице   справа единичную матрицу второго порядка:

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

От второй строки отнимаем две первых:

Первую и вторую строки меняем местами:

От второй строки отнимаем две первых:

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что 

Ответ. 

Замечание

Если на некотором этапе в "левой" матрице получается нулевая строка, то это означает, что исходная матрица обратной не имеет.