Свойства смешанного произведения:

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и   образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

Если векторы  ,   и   заданы своими координатами, то их смешанное произведение вычисляется по формуле

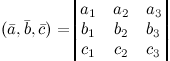
ПРИМЕР. Задание. Вычислить объем пирамиды, построенной на векторах  ,  ,

Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов  ,   и  :

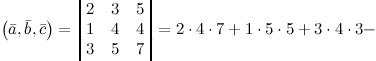
11.3 Условия коллинеарности и компланарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1.

 Два вектора a и b коллинеарны, если существует число nтакое, что

a = n · b

Условия коллинеарности векторов 2.

 Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3.

 Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третьего условия коллинеарности

Пусть есть два коллинеарные вектора a = {a_x; a_y; a_z} и b = {na_x; na_y; na_z}. Найдем их векторное произведение

a × b =	i	j	k	= i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
	ax	ay	az
	bx	by	bz

= i (a_yna_z - a_zna_y) - j (a_xna_z - a_zna_x) + k (a_xna_y - a_yna_x) = 0i + 0j + 0k = 0  Пример .

 Какие из векторов a = {1; 2}, b = {4; 8}, c = {5; 9} коллинеарны?

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

ax	=	ay	.
bx		by

Значит:

Вектора a и b коллинеарны т.к.	1	=	2	.
	4		8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
	5		9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
	4		8

Условия компланарности векторов

• Для 3-х векторов.

 Три вектора компланарны если их смешанное произведение равно нулю.

• Для 3-х векторов.

 Три вектора компланарны если они линейно зависимы.

• Для n векторов.

 Вектора компланарны если среди них не более двух линейно независимых векторов.

Пример

 Проверить компланарны ли три вектора a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.

Решение: найдем смешанное произведение векторов

a · [b × с] =	1	2	3	=
	1	1	1
	1	2	1

= 1·1·1 + 1·1·2 + 1·2·3 - 1·1·3 - 1·1·2 - 1·1·2 = 1 + 2 + 6 - 3 - 2 - 2 = 2

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.