Математика

Вопрос №1 Множества и действия над ними. Диаграммы Эйлера-Венна. Взаимнооднозначное соответствие

1.1Множества и действия над ними.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Множества обозначаются заглавными латинскими буквами  A,B,C …., а элементы множества строчными латинскими буквами  a,b,c...

Запись   означает, что есть множество   с элементами  , которые связаны между собой какой-то функцией   .

Замечание. Элементы в множество входят по одному разу, т.е. без повторений.

Основные операции:

1. Принадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   принадлежит множеству   ).

2. Непринадлежность элемента множеству:

где   -- элемент и   -- множество (элемент   не принадлежит множеству   ).

3. Объединение множеств:   .

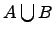Объединением двух множеств   и   называется множество   , которое состоит из элементов множеств   и   , т.е.  или

4. Пересечение множеств:   .

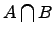Пересечением двух множеств   и   называется множество   , которое состоит из общих элементов множеств   и   , т.е.

   и

5. Разность множеств:   .

Разностью двух множеств   и   , например, множество   минус множество   , называется множество   , которое состоит из элементов множества   , которых нет в множестве   , т.е.  и

6. Симметрическая разность множеств:   .

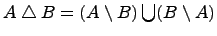Симметрической разностью двух множеств   и   называется множество   , которое состоит из не общих элементов множеств   и   , т.е.

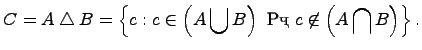
7. Дополнение множества:   .

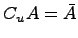Если предположим, что множество   является подмножеством некоторого универсального множества   , тогда определяется операция дополнения:

   и

8. Вхождение одного множества в другое множество:   .

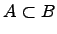Если любой элемент множества   является элементом множества   , то говорят, что множество   есть подмножество множества   (множество   входит в множество   ).

9. Не вхождение одного множества в другое множество:   .

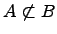Если существует элемент множества   , который не является элементом множества   , то говорят, что множество   не подмножество множества   (множество   не входит в множество   ).

1.2 Диаграммы Эйлера-Венна

Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

О пределение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

 

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые

Принадлежат одновременно как множеству А, так и множеству В (рис.2)

 

О пределение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

 

О пределение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):