Значение моделирования:

1. Гипотезы об объекте, выраженные математически, могут служить количественным описанием биологических, сельскохозяйственных и других объектов (процессов) и тем самым способствуют более углубленному их пониманию.

2. Математическая модель часто подсказывает способ представления результатов научных исследований в форме, удобной для использования в практике (графики, гистограммы).

3. Благодаря модели может быть количественно оценена экономическая эффективность внедрения нового объекта или процесса в производство.

4. Позволяет выбрать оптимальную стратегию воздействия на объект.

5. Дает возможность сократить объем дальнейших экспериментальных работ с объектом.

6. При исследовании сложных объектов модель позволяет объединить разрозненные знания об отдельных частях системы в единое целое.

7. С помощью модели можно выбрать наиболее рациональную стратегию и тактику реализации исследовательских программ (теория планирования эксперимента).

8. Математическая модель – это мощное средство обобщения разнородных данных об объекте, позволяющее осуществлять как интерполяцию (восстановление недостающей информации о прошлом), так и экстраполяцию (прогнозирование будущего поведения объекта).

В основе любой математической модели и метода ее анализа лежит математический аппарат. Это могут быть дифференциальные уравнения, формулы теории вероятностей, математической статистики и т.д. Правильный подбор математического аппарата – необходимое условие построения удачной модели.

Вопросы:

1. Что такое моделирование, общее определение модели, для чего их используют?

2. Приведите классификацию моделей и определения математической модели.

3. В чем разница понятий робастности и адекватности модели?

4. Что такое настройка модели и как она проводится?

5. Чем отличаются дискриптивные и оптимизационные модели?

2. Модели динамики биологических систем.

2.1. Прогрессия размножения.

Приведем несколько приложений дифференциальных уравнений для моделирования биологических систем и процессов.

Ещё Ч. Дарвин обратил внимание на стремление каждого вида к размножению в геометрической прогрессии. То есть каждая пара организмов дает гораздо больше потомства, чем их выживает до взрослого состояния. Это явление потенциального возрастания численности каждого вида получило название прогрессии размножения. Всю эволюцию можно рассматривать, как ограничение на избыточное размножение.

Рассмотрим два типа моделей, с помощью которых можно глубже понять последствия прогрессии размножения и ограничений на неё. Эти несложные математические модели применяются в эволюции, генетике, экологии, биофизике, демографии, медицине и т.д.

Для рассмотрения прогрессии размножения в простейших ситуациях можно не учитывать генетическую структуру популяции, а сконцентрировать все внимание на изменении численности популяции N во времени t.

Основной показатель, характеризующий популяцию определён­ного вида – скорость естественного увеличения популяции (r). Это среднее число потомков, возникающих от одной особи популяции за единицу времени.

r=b-d, где b – средняя рождаемость на одну особь за единицу времени; d – средняя смертность в пересчёте на одну особь за единицу времени.

Пример. Популяция состоит из 800 особей. В среднем за год рождается 150 особей, а умирает 50. Определить скорость естественного увеличения популяции (r). Ответ: r = 150/800 – 50/800 = 0,125 1/год.

Изменение численности популяции во времени можно выразить через скорость . Сама скорость также как и численность может меняться во времени. То есть чем больше численность популяции в данный момент времени, тем выше скорость увеличения численности (как и в примере с рыбами в начальный период роста популяции).

Основное уравнение, описывающее прогрессивное размножение, когда нет никаких ограничений на N:

Решение этого уравнения: N_t=N₀e^rt, где N₀ – начальная численность популяции; е – основание натурального логарифма.

Графически решение представлено на рисунке.

Эта модель справедлива для достаточно большого исходного значения N₀, когда дискретным характером численности можно пренебречь.

N_t

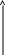
N₀

t

Error: Reference source not found

Задача. Для первой популяции r - скорость естественного увеличения равна 0,1 1/год, а для второй 0,05 1/год. Начальная численность второй популяции в 2,72 больше начальной численности первой. Определить, через какой промежуток времени численности обеих популяций сравняются.

Схема решения.

r₁ = 0,1 1/год; r₂ = 0,05 1/год; N₀₂ = 2,72N₀₁

Ответ: t = 20 лет.

Можно привести примеры оценок N_t для разных видов в предположении отсутствия ограничения на численность. Так, потомство одной особи бактерии Фишера (r  100 1/час) покроет Землю одним слоем менее чем за 2 суток. За 1300 лет потомство одной пары слонов образовало бы слой 15 км высотой. Потомство одного растения мака при комфортных условиях покроет всю Землю за 3-4 года.

Подобные потенциальные способности видов к прогрессивному размножению вызывает так называемое «давление жизни», и, как следствие конкуренцию, борьбу за существование между особями, популяциями, видами и т.д. Это фундамент естественного отбора.

Вследствие естественных абиотических и биотических факторов возникают ограничения скорости роста численности популяций. Наиболее простой вариант (для моделирования) – это стабилизация N_t на некотором максимально допустимом уровне K_max из-за ограниченности ареала обитания популяции.

В модели такое предположение можно отразить, добавив к левой части основного уравнения прогрессии размножения множитель (1-N/K_max) :

Соответствующий график зависимости N_t от t представлен на рисунке а.

Рис. а

N_t

K_max

N₀

t

При численности N, малой по сравнению с K_max, дополнительный множитель близок к 1 и практически не влияет на зависимость N от t. По мере роста численности и приближения N к K_max множитель, а значит и вся левая часть уравнения, приближается к 0. Следовательно скорость роста популяции также стремиться к нулю: кривая роста выходит на плато N_t = K_max.