2. Определение расчетных частот вращения и моментов на валах для расчета на прочность

За расчетную частоту вращения шпинделя принимается частота, на которой на шпиндель передаются наибольшая мощность и наибольший крутящий момент (n_р=116мин^-1). Как правило, она соответствует номинальной частоте вращения двигателя и низшему диапазону .

Расчетные моменты на валах и шпинделе корректируем с учетом уточненных величин передаточных отношений и КПД :

М₁=М^н_дв=327Нм;

,

где _1-2 – КПД между валами 1 и 2. _1-2 =_ЗП²_ПК=0,99∙0,995²=0,98;

.

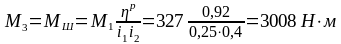3. Определение усилий в зубчатых передачах

Знание этих сил необходимо для расчета зубьев, валов и их опор. Для цилиндрических прямозубых колес окружное усилие

P_t = 2∙10³ M/d [H],

где: М – передаваемый крутящий момент, Н∙м;

Радиальное усилие

P_r = P_t tg(α+ρ)≈0,5 P_t ,

(где α и ρ соответственно углы зацепления и трения).

где β – угол наклона зубьев.

для передачи 1-2:

Р_t¹²=2∙10³∙327/130=5030Н;

Р_r¹²=0,5∙ Р_t¹²=0,5∙5030=2515Н.

для передачи 3-4 между валом II и шпинделем:

Р_t³⁴=2∙10³∙1281/150=17080Н;

Р_r³⁴=0,5∙ Р_t¹²=0,5∙17080=8540Н.

5. Расчеты деталей на прочность и жесткость

   1. Расчет цилиндрических зубчатых передач

При курсовом проектировании производится расчет одной зубчатой передачи на выносливость при изгибе и контактную прочность. Расчетные формулы и коэффициенты даны на базе ГОСТ 21354-87 .

6.1.1. Расчет зубьев на выносливость при изгибе

Расчетное напряжение для зубьев шестерни z₃=26 определяем по формуле для прямозубых передач.

.

Здесь: М=М₂=1281Нм – расчетный крутящий момент на валу II (колесе z₃);

b=65мм – ширина венца по основанию зуба;

d=150мм – делительный диаметр колеса z₃;

m=6мм – модуль;

k_FV – коэффициент, учитывающий динамическую нагрузку в зацеплении.

Окружная скорость при расчетной частоте вращения n_II=495мин^-1 (см. раздел 6)

.

Для степени точности 6 - k_FV =1,;

k_Fβ - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. k_Fβ=1,15.

Y_F – коэффициент формы зуба. Для некорригированных колес выбирается по табл. 7.3., для корригированных – по рекомендациям [12,14].

Для колеса z₃ = 265 Y_F = 3,9(интерполируя по значениям z=17…26).

Y_ε=1 – коэффициент, учитывающий перекрытие зубьев.

Аналогично производится расчет для парного колеса z₄=100.

Допускаемое напряжение изгиба для шестерни z₃=25:

σ_FР=σ_Flimb∙ k_Fg∙ k_FC∙k_FL∙1/S_F=750∙0,7∙0,75∙1∙1/1,65=240Н/мм².

Здесь _Flimb=750 Н/мм² - длительный предел выносливости зубьев при изгибе, соответствующий базовому числу циклов (см. приложение 5. – в зависимости от материала и термообработки.

K_Fg=0,7 – коэффициент, учитывающий влияние шлифования переходной поверхности зуба после термообработки.

Принимается K_Fg=0,7 для цементированных колес и K_Fg=1,0 в остальных случаях.

K_FC=0,75 – коэффициент, учитывающий работу зубьев при реверсивной нагрузке (при нагрузке в одну сторону K_Fc=1,0).

K_FL=1,0 – коэффициент режима нагружения и долговечности (для случая интенсивной эксплуатации привода).

S_F=1,65 – коэффициент безопасности. Определяется в зависимости от вероятности неразрушения и свойств заготовки [12, 14]. При курсовом проектировании принимать S_F=1,6…1,8.

Аналогично определяем допускаемое напряжение колеса Z₄=100.

Сравнения расчетного напряжения изгиба _F=165 Н/мм² с допускаемым _FP=240 Н/мм² показывает, что изгибная прочность передачи обеспечена с запасом.