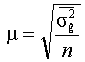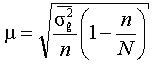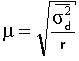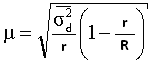- •Экзамен по дисциплине «Статистика»
- •Раздел 1. Общая теория статистики. 4
- •Раздел 2. Социально-экономическая статистика 90
- •Раздел 1. Общая теория статистики.
- •Предмет статистической науки, ее теоретические основы. Связь статистической науки с другими экономическими дисциплинами.
- •Особенности статистической методологии. Закон больших чисел и статистическая закономерность.
- •Значение и основные задачи статистики в современных условиях.
- •Стадии статистического исследования. Их краткая характеристика.
- •Основные понятия и категории статистической науки.
- •Современная организация статистики в Российской Федерации. Задачи органов статистики.
- •Понятие о статистическом наблюдении и его задачи. Две формы организации статистического наблюдения.
- •Программно-методологические вопросы статистического наблюдения.
- •Важнейшие организационные вопросы статистического наблюдения.
- •Виды статистического наблюдения.
- •Общие понятия о статистической сводке и ее задачи. Организация и техника проведения сводки.
- •Метод группировок и задачи, решаемые с помощью группировок.
- •Виды группировок, их краткая характеристика.
- •Понятие и виды рядов распределения. Графическое изображение рядов распределения.
- •Абсолютные статистические величины, их значение, виды и единицы измерения.
- •Относительные статистические величины, их значение, единицы измерения и виды.
- •Общая характеристика и методика расчета относительных величин планового задания, выполнения плана и динамики. Статистическое изучение взаимосвязи между относительными величинами.
- •Общая характеристика и методика расчета относительных величин структуры, сравнения и координации. Относительные величины интенсивного и уровня экономического развития.
- •Сущность и значение средних в статистике, их виды.
- •Средняя арифметическая, ее свойства и методика расчета.
- •Средняя гармоническая, методика ее расчета. Выбор формы средней.
- •Структурные средние, их виды и методика расчета в рядах распределения.
- •Понятие о вариации, виды показателей вариации, методика расчета.
- •Виды дисперсий, методика их расчета. Правило сложения дисперсии.
- •Ряды динамики и их виды. Причины несопоставимости уровней ряда динамики.
- •Показатели ряда динамики, методика расчета базисных и цепных показателей ряда динамики.
- •Расчет средних показателей ряда динамики.
- •Механические методы выявления основной тенденции развития, их характеристика.
- •Аналитическое выравнивание ряда динамики, методика его проведения.
- •Понятие сезонности и статистические приемы изучения сезонных колебаний.
- •Определение индекса, сфера применения индексов в статистике. Классификация индексов.
- •Понятие индивидуальных и общих индексов, методика их расчета.
- •В каждом индексе выделяют 3 элемента:
- •Индивидуальный индекс физического объема товарооборота
- •Индивидуальный индекс цен
- •Индивидуальный индекс товарооборота
- •Формы индексов. Агрегатный индекс как основная форма экономического индекса.
- •Методика расчета средних индексов.
- •Статистическое изучение динамики среднего уровня. Методика расчета и экономический смысл индексов динамики среднего уровня.
- •Взаимосвязь индексов. Изучение влияния различных факторов при помощи индексного метода.
- •Понятие о выборочном наблюдении и его задачах, основные этапы проведения выборочного наблюдения и практика его применения в статистике.
- •Методы и способы отбора единиц в выборочную совокупность.
- •2) Механический
- •4) Серийный
- •5) Комбинированный
- •Понятие об ошибках выборки. Формулы расчета средних и предельных ошибок выборки.
- •Определение необходимой численности выборки и распространение результатов выборки на генеральную совокупность.
- •Роль статистики в исследовании взаимосвязей. Виды и формы взаимосвязей.
- •Индексный метод исследования статистической взаимосвязи.
- •Раздел 2. Социально-экономическая статистика
- •Предмет метод и задачи социально-экономической статистики.
- •Определение численности и состава населения.
- •Показатели естественного и механического движения населения. Расчет перспективной численности населения.
- •Понятие и состав трудовых ресурсов, трудоспособного и занятого населения.
- •Показатели и состав экономически активного и экономически неактивного населения, группировка экономически активного населения по статусу в занятости.
- •Категории численности и состава работников промышленного предприятия.
- •Показатели статистики использования рабочего времени.
- •Затраты на рабочую силу. Понятие и состав фонда заработной платы.
- •Анализ динамики фонда заработной платы с выделением отдельных факторов.
- •Понятие основных фондов, их классификация.
- •Виды оценки основных фондов. Балансы основных фондов. Переоценка основных фондов.
- •2. Виды оценки основных фондов. Балансы основных фондов
- •3. Потребление основного капитала. Амортизация основных фондов. Методы начисления амортизации
- •4. Показатели состояния, движения и использования основных фондов
- •Понятие амортизации. Расчет суммы и норм амортизации.
- •Показатели, движения и использования основных фондов.
- •1. Показатели состояния оф:
- •2. Показатели динамики оф:
- •Анализ динамики средней фондоотдачи (индексы переменного, постоянного состава и структурных сдвигов).
- •Анализ динамики объема продукции за счет изменения фондоотдачи, стоимости основных фондов и структуры основных фондов.
- •Понятие оборотных средств.
- •Изучение объема, состава и структура себестоимости продукции.
- •Изучение материалоемкости продукции.
- •Сущность ввп. Методы определения ввп.
- •Понятие валового выпуска и промежуточного потребления.
- •Прямые и обратные показатели уровня производительности труда, их динамика.
- •Натуральный метод измерения уровня и динамики производительности труда.
- •Трудовые индексы производительности труда.
- •Экономический смысл и методология расчета стоимостных индексов производительности труда.
- •Показатели уровня и динамики среднечасовой, среднедневной и среднегодовой выработки, их взаимосвязь.
- •Влияние изменения уровня производительности труда и численности работающих на изменение объема продукции.
- •Понятие эффективности общественного производства. Методология исчисления обобщающих показателей эффективности общественного производства.
- •Система показателей статистики уровня жизни. Индекс потребительских цен.
- •Показатели доходов населения.
- •Показатели потребления и расходов населения.
2) Механический
Состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в ген. сов. равен обратной величине доли выборки.
(Формулы такие же, как и у собственно-случайной)
3) Типический (увеличивает точность результатов)
Ген. сов. вначале расчленяется на однородные типические группы. Затем из каждой такой группы собст.-случ. или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Средняя ошибка выборки |
Повторный отбор |
Бесповторный отбор |
Для среднего |
|
внутригрупповая |
4) Серийный
Такой вид формирования выборочной совокупности, когда все случайном порядке собираются не единицы, а группы единиц, подлежащие обследованию (серии). Внутри серий обследованию подвергаются все единицы.
Средняя ошибка выборки |
Повторный отбор |
Бесповторный отбор |
Для среднего |
r – число отобранный серий |
R – число серий в ген. Сов. |
5) Комбинированный
Прибегают для обеспечения наибольшей репрезентативности (выборки) с наименьшими трудовыми и денежными затратами на организацию и проведение обследования. (сочетание выборок)
![]()
Интервальная характеристика ген. совокупности:
![]()
![]()
Понятие об ошибках выборки. Формулы расчета средних и предельных ошибок выборки.
Ошибка репрезентативности (выборки) – это расхождение между выборочной хар-ой и хар-ой ген. сов.
Ошибки выборки |
|||
Систематические |
Случайные |
||
преднамеренные |
непреднамеренные |
средняя о.в. |
Предельная о.в. |
Средняя ошибка выборки – это такое расхождение между характеристикми выборочной и ген. сов., которые не превышает ±σ.
Для среднего: для количественного признака |
Для доли: для альтернативного признака |
|
|
- чем больше численность, тем меньше ошибка;
- чем больше дисперсия (вариация признака), тем выше ошибка выборки.
Предельная ошибка – это мах возможное расхождение выборочной и ген. хар-ик (мах ошибки).
Для среднего |
Для доли |
|
|
t – коэф. доверия, значение которой зависит от вероятности:
Вероятность F(t) |
t |
0,683 |
1 |
0,905 |
1,96 |
0,954 |
2 |
0,99 |
2,58 |
0,997 |
3 |
Пример: В 3 случаях из тысячи мы можем ошибиться. Чем выше t, тем выше оценка.
Определение необходимой численности выборки и распространение результатов выборки на генеральную совокупность.
Величина
![]() (дисперсия
признака) в ген совокупности часто
бывает неизвестна. Используют приближенные
способы оценки ген. дисперсии.
(дисперсия
признака) в ген совокупности часто
бывает неизвестна. Используют приближенные
способы оценки ген. дисперсии.
1) Можно провести пробное обследование (небольшого объема), на базе которого опред. величина дисперсии признака, используемая в качестве оценки ген. дисперсии.
проб. – сред. ариф. По результатам пробного обследования
n проб. – число ед., попавших в пробное обследование.
По данным нескольких пробных обследований выбирается наибольшее значение дисперсии.
![]()
2) Можно использовать данные прошлых выборочных обследований, проводившихся в аналогичных целях.
3) Если распред. признака в ген. сов. может быть отнесено к нормальному закону распр., то размах вариации примерно равен 6σ или R≈6σ, где R=Хмах-Хmin.
Пример:
Сколько операционалистов нужно обследовать в банках региона, чтобы получить характеристику среднего уровня оплаты труда этой категории работников банка в регионе?
Разница между мах и min уровнем оплаты труда = 300 тыс. руб.
Т.о. σ ≈300/6 = 50 тыс. руб. Ошибка не должна превышать 10 тыс. руб. Зная, что σ = 50 тыс. руб., а t=2, получим по формуле: n = t^2*σ^2 / ∆^2 x.
n = 2^2 * 50^2 / 10^2 = 100 человек.
Средняя ошибка выборки |
Повторный отбор |
Бесповторный отбор |
Для среднего (частность ω неизвестна, вводится мах величина дисперсии = 0,25) |
n
= t^2 /4 *
|
n = t^2N / 4N + t^2 |
Для доли |
n = t^2* ω (1-ω) / |
n = t^2 ω (1-ω)N / N +tω(1-ω) |