7.Екстремум ф-ї 2х змінних. Необхідна і достатня умови екстремуму.

Т. М_о(х_о;у_о) наз т max (min) ф-ї f(х;у) в обл. Д , якщо для любої точчки М(х;у) із дельта околу т М_о(х_о;у_о) значення ф-ї в т М_о найбільше(найменше).

Точка М_о, в якій ф-я має екстремум наз т екстремуму. Max (min) ф-ї наз її екстремумом.

Необхідна умова існування екстремуму:

Я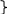 кщо диференційована ф-я f(х;у) досягає екстремума в т (х_о;у_о) то її частинні похідні 1-го порядку в цій точці =0 або не існують.

∂f/∂x=0

∂f/∂у=0

Точки в яких частинні похідні = 0 або не існують наз критичними (стаціонарними).

Але не кожна стаціонарна точка є точкою екстремуму, а тому кожна стаціонарна точка повинна бути перевірена на екстремум за допомогою достатніх умов.

Достатні умови існування екстремуму.

I Нехай функція має неперервні частинні похідні до другого порядку включно в деякій області, що містить критичну точку . Тоді:

а) якщо в точці , то функція має в цій точці екстремум; причому це буде мінімум, якщо , і максимум, якщо ;

б) якщо , то екстремуму в цій точці немає;

в) якщо , то потрібні додаткові дослідження, оскільки екстремум може бути, а може й не бути.

II Нехай – критична точка функції . Тоді, якщо за умови , другий диференціал , то в точці функція має максимум, якщо , то – мінімум, а якщо змінює знак, тоді екстремуму в цій точці немає.

8.Умовний екстремум ф-ї 2х змінних. Метод множників Лагранжа.

Н ехай дано ф-ю Z=f(х;у) і L є Д. Потрібно знайти ext ф-ї Z=f(х;у) в точках , що належать L ліній.

Умовним ext ф-ї Z=f(х;у)наз екстремум цієї ф-ї, досягнутий при умові, що змінні х і у зв’язані рівнянням.У(х;у)=0 (рівняння зв’зку).

Z=f(х;у)

Уf(х;у)=0

Для знаходження точок ext використовують 2-а способи.

1)Поставлена задача зводиться до знаходження екстремуму ф-ї 1-ї змінної .Для цього треба розв’язати рівняння зв’язку відносно х або у і це значення підставити у ф-ю Z. у=у₁(х) Z=f(х;у₁(х))=f(х)—дослідити на ext.

2)Якщо із рівняння зв’язку складно знайти один із аргументів , то точки ext знаходять за методом множників Лагранжа.

Склад. Ф-я Лагранжа

U= f(х;у)+У(ху), —const.

К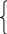 ритичні точки визначаються із системи:

∂u/∂х=0

∂u/∂у=0

∂u/∂=0

9. Найбільше і найменше значення функції 2-ох змінних у замкнутій області)

Найбільше значення функції – це саме більше із усіх можливих її значень. Відповідно найменше значення функції – це саме менше із усіх можливих її значень.

В ряді задач потрібно знайти найбільше і найменше значення функції z в деякій замкнутій області D. Якщо ця функція неперервна в замкнутій області D, то за теоремою Вейєрштрасса вона приймає в D свої найменше і найбільше значення.

Для цього потрібно:

1. Знайти критичні точки, що розташовані в області D.

2. Обчислити значення функції в цих критичних точках.

3. Знайти найбільше і найменше значення на лініях, що утворюють границю області D.

4. З усіх знайдених значень вибрати найбільше і найменше значення.

10. Диференціальні рівняння. Основні поняття і означення. Задача Коші.

Звичайним диф. рівнянням наз. р-ня, яке містить незал. змінну х,шукану ф-ю y=y(x) та похідну шуканої ф-ї до деякого порядку включно. Загальний вигляд: F(x,y,y’,y’’….y⁽ⁿ⁾)=0.

Порядком диф. р-ня наз. найвищий порядок похідної,що входить в дане р-ня.

y’+xy=0(диф.р-ня першого порядку); y’’+2y’+4y=sinx(диф.р-ня 2-гопорядку).

Рішенням диф.р-ня наз. всяка ф-я y=j(x),яка при підстановці в дане р-ня перетв.його в тотожність, тобто F(x, j(x), j’(x), j’’(x)… j⁽ⁿ⁾(x))=0.

Загальним розв’язком диф. р-ня n-го порядку наз. р-ня аргумента x і n довільних констант c₁,c₂…..c_n,тобто y=j(x, c₁,c₂…..c_n) при підстановці якої вдане р-ня одержуємо тотожність.

Частинним розв’язком диф. р-ня любого порядку наз.таке рішення р-ня, яке одержано із загального при фіксованих значеннях const, тобто:y= j(x, c₁⁰,c₂⁰,….c_n⁰),де c₁⁰,c₂⁰,….c_n⁰-конкретні числа.y=c₁e^x+c₂xe^x- загальне р-ня. Так, якщо y=c₁e^x+c₂xe^x –заг.розв’язок диф.р-ня,то якщо с₁=0,а с₂=1,то y^--=xe^x частинний розв’язок р-ня. Щоб одержати частинний розв’язок із загального, вводять додаткові умови, які наз. початковими умовами диф. р-ня.

Загальний вигляд початкових умов для:а) диф. р-ня 1-го порядку:y(x₀)=y_0. б) для 2-го порядку: y(x₀)=y_0, y’(x₀)=y’_0. Знаходження частинного розв’язку диф. р-няпо заданим початковим умовам наз. задачею Коші. Теорема про існування і єдність розв’язку задачі Коші завжди мають розв’язок і притому єдиний,зокрема для р-ня 1-го порядку. Якщо права частина р-ня y’=f(x,y) як ф-я двох змінних визначена і неперервна в обл..Д, що містить т.М₀(x₀,y₀) і має неперервні частинні похідні f’_x, f’_y в цій точні, причому f’_y≠0.

11.Диф. р-ня 1-го порядку з відокремленими змінними.

F(x,y,y’)=0 –диф.р-ня 1-го порядку в заг.вигляді. y’=f(x,y). Якщо права частина р-ня y’=f(x,y) може бути представлена у вигляді добутку двох співмножників,один із яких не містить змінної х,а другий не містить змінної у,то f(x,y)= f₁(x)f₂(у),тоді р-ня y’=f(x,y) набуде вигляду: y’= f₁(x)f₂(у), яке наз. диф. р-ням з відокремленими змінними. Метод розв’язанні: відокремлення змінних з наступним інтегруванням. у’=dy/dx,dy/dx= f₁(x)f₂(у) | x dx/ f₂(у). dy/ f₂(у)= f₁(у)dx. ∫ dy/ f₂(у)=∫ f₁(x)dx +c₁-загальний розв’язок р-ня y’= f₁(x)f₂(у).

Заув. Якщо загальний розв’язок одержимо у вигляду наявноє ф-ї, то його наз. загальним інтегралом.