78.Функція дискретної випадкової величини. Закон розподілу функції, числові характеристики.

Нехай в результаті випробувань спостерігаються значення в.в. Х і У.Сукупність в.в. (Х;У), які розглядаються в сукупності наз. системою двох випадкових величин або двовимірною в.в. ДВВ можна геометрично втлумачити як вип.. точку М(х у) на площині або як вип. вектор ОМ(х,у). Якщо в.в. Х і У дискретні, то і двовимірна в.в. наз. дискретною. Якщо ж в.в. ХУ неперервні, то і ДВВ (ХУ) наз. неперервною. Задати ДВВ (ХУ) дискретного типу можна за допомогою закону розподілу або ф-ції розподілу.Всяке співвідношення, яке встановлює зв'язок між можливими значеннями ВВ(ХУ) і відповід. їм ймовірност. наз. законом розподілу системи ВВ.

Найпростішою формою закону розподілу ВВ(ХУ) дискретного типу є таблиця з подвійним входом, що містить всі можливі пари значень (Х_іУ_j) ВВ(ХУ) з відповідними їм ймовірностями, Р_ij=Р(Х=х_і, У=у_j) що задовольняють умові

79.Визначення щільності розподілу функції неперервної випадкової величини по щільності розподілу аргументу.

Нехай випадкова величина   має диференційовану функцію розподілу ймовірностей   , Тоді функція   (33.1)  називається щільністю розподілу ймовірностей (або щільністю ймовірності) випадкової величини   , А випадкова величина   - Безперервної випадкової величиною.  Розглянемо основні властивості щільності ймовірності.  З визначення похідної слід рівність:   . (33.2)  Згідно властивостям функції   має місце рівність   . Тому (33.2) набирає вигляду:   . (33.3)  Це співвідношення пояснює назву функції   . Дійсно, згідно (33.3) функція   - Це ймовірність   , Що припадає на одиницю інтервалу   , В точці   , Оскільки   .

Це співвідношення має важливе значення для додатків, оскільки дозволяє обчислити вірогідність   через щільність ймовірності   або через функцію розподілу ймовірностей   . Якщо покласти   , То з (33.7) слід співвідношення (33.6).  На рис. 33.1 наведені приклади графіків функції розподілу та щільності ймовірностей. 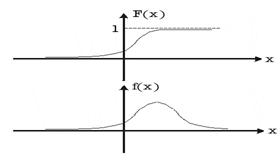 Рис. 33.1. Приклади функції розподілу ймовірностей і щільності ймовірності.  Відзначимо, що щільність розподілу ймовірності може мати кілька максимумів. Значення   аргументу   , При якому щільність   має максимум називається модою розподілу випадкової величини   . Якщо щільність   має більш однієї моди, то   називається багатомодальну.