46. Формула Бейєса.

Баєсів підхід не робить припущень про ймовірності елементарних подій, а намагається отримати їх із аналізу попереднього досвіду, спираючись на теорему Баєса і на попередні гіпотези. Оскільки ці ймовірності наперед невідомі, результати серії дослідів розбиваються на сприятливі й несприятливі, і експериментально визначена ймовірність дорівнює відношенню числа сприятливих подій до числа дослідів, тобто частоті подій. Теорема Байєса – одна з осн. теорем елементарної теорії ймовірності, яка визначає ймовірність настання події в умовах, коли на основі спостережень відома лише деяка часткова інформація про події. За допомогою формули Байєса можно більш точно обчислювати ймовірність, взявши до уваги як і раніше відому інформацію так і дані нових спостережень.

47.Повторні незалежні випробування. Формула Бернуллі.

Нехай проводяться n випробувань, у кожному з яких подія А може як відбутись, так і не відбутись. Якщо ця ймовірність у кожному випробуванні не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називаються незалежними щодо події А. Згідно з означенням випробування також незалежні, якщо в кожному з них імовірність настання події А однакова, тобто дорівнює тому самому числу. Імовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають а ймовірність настання протилежної події

Формула Бернуллі.

Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:

Формула застосовується, якщо

Імовірність того, що в результаті n незалежних експериментів подія А з’явиться від mi до mj раз, обчислюється так:

48. Наймовірніше число появи події в незалежних випробуваннях.

У формулі Бернуллі параметр m може змінюватися від 0 до n, тобто в n-випробуваннях подія А може зявитися 0 (жодного разу) до n (зявится в кожному випробуванні) з різними ймовірностями обчисленими за формулою Бернуллі: Pn(m)=Cnm pmqn-m

Число m для якого ймовірність Pn(m) є найбільшой називаєтся наймовірнішим числом настання події. Наймовірніше число настання події знаходиться: np-q ≤ m0 ≤ np+p

Зауваження:

1.) Якщо np-q – число дробове, то існує одне наймовірніше число n0, воно =найближчому цілому до m0 зправа;

2.) Якщо np-q – є ціле, то існує два наймовірніші числа m0 та m0+1, де m0= np-q

49. Локальна теорема Муавра-Лапласа.

Рассмотрим последовательность из n независимых опытов, в каждом из которых событие A может произойти с вероятностью p,либо не произойти — с вероятностью q = 1 − p. Обозначим через P_n(k)вероятность того, что событие A произойдет ровно k раз из n возможных.В таком случае величину P_n(k) можно найти по теореме Бернулли

Эта теорема прекрасно работает, однако у нее есть недостаток. Если n будет достаточно большим, то найти значение P_n(k) становится нереально из-за огромного объема вычислений. В этом случае работает Локальная теорема Муавра — Лапласа, которая позволяют найти приближенное значение вероятности. Імовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:

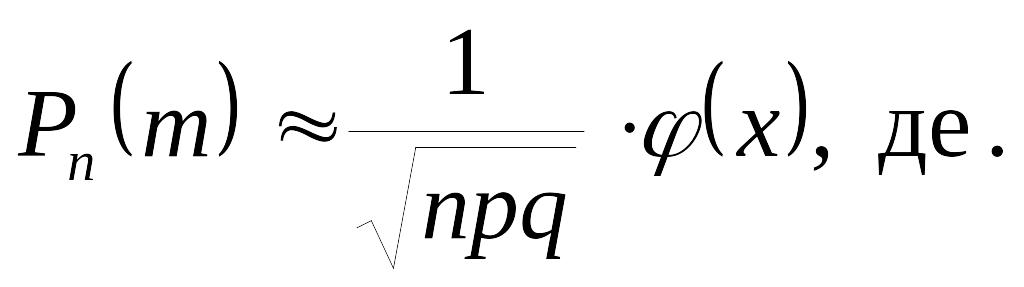
Локальна теорема Лапласа дає змогу обчислювати ймовірності , якщо n > 10 i p > 0,1.