Методы общего анализа линейных электрических цепей с несколькими источниками

Важным вопросом этого раздела является расчет распределения токов в сложных линейных цепях с несколькими источниками. Клас­сическим методом расчета таких цепей является непосредственное применение законов Кирхгофа. Все остальные методы расчета исхо­дят из этих фундаментальных за­конов электротехники.

Рассмотрим сложную элек­трическую цепь (рис. 4), которая содержит шесть ветвей. Если бу­дут заданы значения всех э. д. с. и сопротивлений резисторов, а по условию задачи требуется опреде­лить токи в ветвях, то имеем за­дачу с шестью неизвестными. Та­кие задачи решаются с помощью

законов Кирхгофа. В этом случае должно быть составлено столько уравнений, сколько неизвестных токов.

Порядок расчета следующий.

1. Если цепь содержит последовательные и параллельные соеди­нения, то ее упрощают, заменяя эти соединения эквивалентными.

2. Произвольно указывают направления токов во всех ветвях. Если принятое направление тока не совпадает с действительным, то при расчете такие токи получаются со знаками минус.

3. Составляют (п—1) уравнений по первому закону Кирхгофа {п — число узлов).

4. Недостающие уравнения в количестве т - (n— 1), где т — число ветвей, составляют по второму закону Кирхгофа, при этом обход контура можно производить как по часовой стрелке, так и против нее. За положительные э. д. с. и токи принимаются такие, на­правление которых совпадает с направлением обхода контура. На­правление действия э. д. с. внутри источника всегда принимают от минуса к плюсу (см. рис. 4).

5. Полученную систему уравнений решают относительно неизвест­ных токов. Составим расчетные уравнения для электрической цепи изображенной на рис. 4. Выбрав произвольно направление токов в ветвях цепи, составляем уравнение по первому закону Кирхгофа для a,b,c

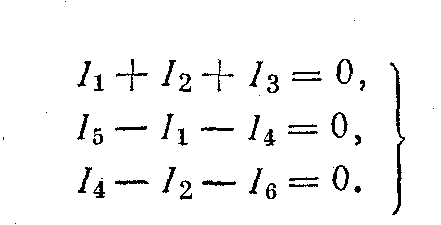
Приняв направление обхода контуров по часовой стрелке, составляем уравнения по второму закону Кирхгофа для трех произвольно выбранных контуров:

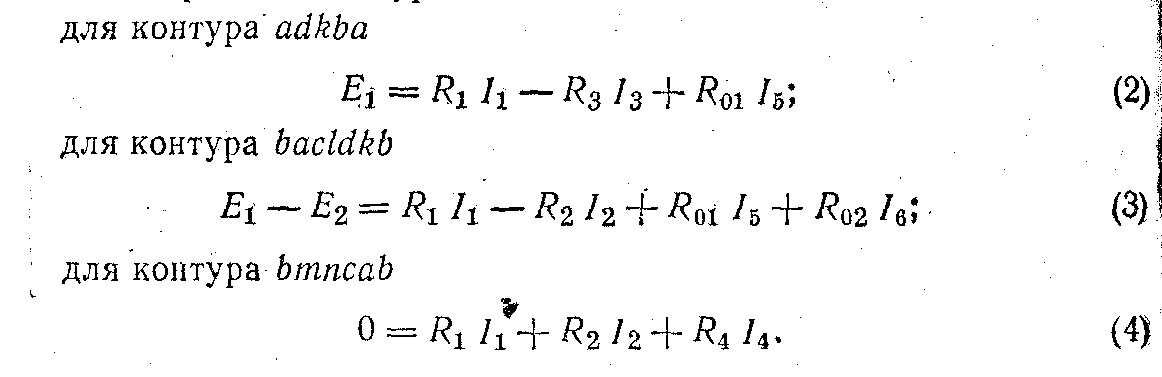
Решая совместно уравнения (1), (2), (3) и (4), определяем то­ки в ветвях электрической цепи.

Легко заметить, что решение полученной системы из шести урав­нений является весьма трудоемкой операцией. Поэтому при анализе электрических цепей с несколькими источниками целесообразно при­менять метод контурных токов (метод ячеек), позволяющий умень­шить число совместйо решаемых уравнений, составляемых по двум законам Кирхгофа, на число уравнений, записанных по первому зако­ну Кирхгофа. Следовательно, число уравнений, составляемых по ме­тоду контурных токов, равно m—n+1. При решении этим методом количество уравнений определяется числом ячеек. Ячейкой назы­вают такой контур, внутри которого отсутствуют ветви. В данном случае таких контуров-ячеек три: badkb, aclda, mncabm.

Расчет сложных электрических цепей методом контурных токов

ведется следующим образом.

1. Вводя понятие «кон­турный ток», произвольно за­даемся направлением этих то­ков в ячейках. Удобнее все токи указать в одном направлении, например по часовой стрелке (рис. 5).

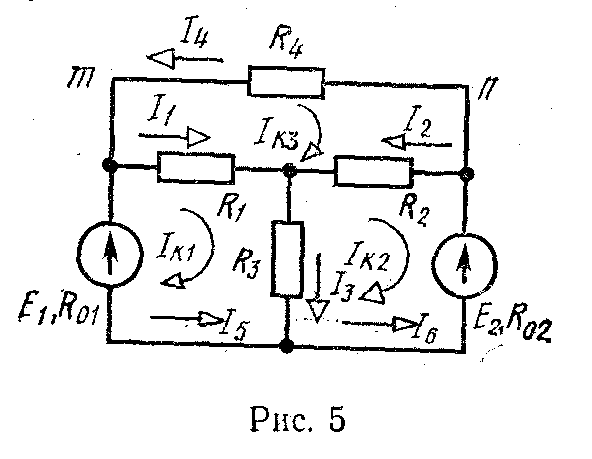
2. Составляем для каждого контура-ячейки уравнение по второму закону Кирхгофа. Обход контуров производим по часовой стрелке:

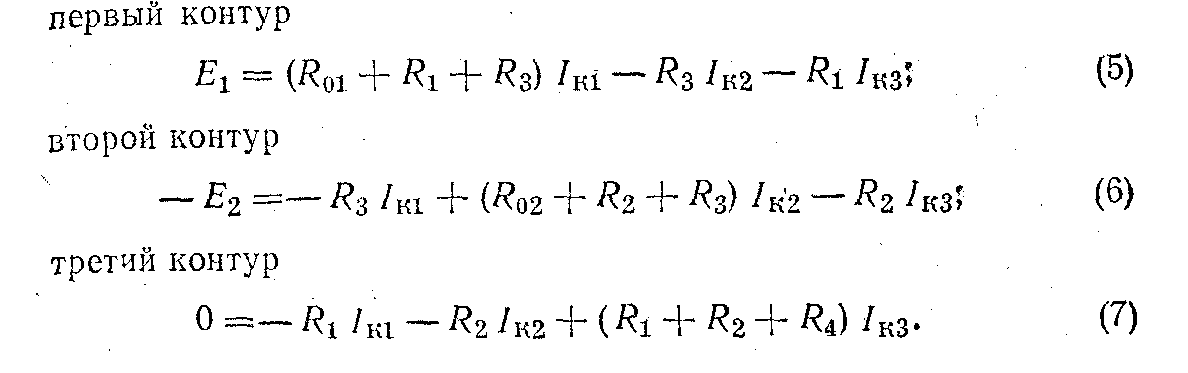
3. Решая совместно уравнение (5), (6), (7), определяем контур­ные токи. В том случае, когда контурный ток получается со знаком минус, это означает, что его направление противоположно выбран­ному на схеме.

4. Токи во внутренних ветвях схемы определяются как сумма или разность соответствующих контурных токов. В том случае, ког­да контурные токи в ветви совпадают, берут сумму, а когда направ­лены навстречу — из большего тока вычитают меньший.

5. Токи во внешних ветвях схемы по значению равны соответст­вующим контурным токам.

Задача 1. Найти токи в цепи, схема которой изображена на рис. 5.

Задано: E1=100, E2=120, R01=R02=0,5 Ом, R1=5 Ом, R2=10 Ом, R3=2 Ом, R4=10 Ом

Определить токи в ветвях цепи.

Решение. Используя уравнения (5), (6) и (7), получаем;

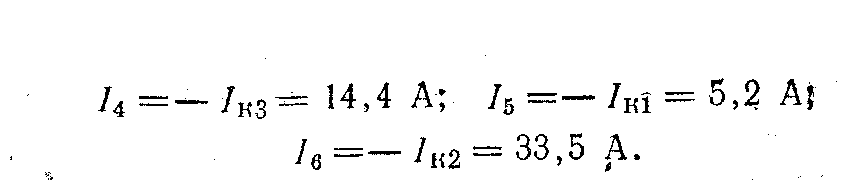
Задача 2. Определить токи и составить баланс мощностей для схемы, изображенной на рис. 6. Дано:

J=50 мА, E=60 В, R1 = 5 кОм,

R₂ = 4 кОм, Rз=16 кОм, R₄ = = 2 кОм, R₅ = 8 кОм.

Решение. Схема содержит шесть ветвей (m=6) и четыре уз­ла (n = 4). Число уравнений, со­ставляемых по методу контурных токов, равно, т—п+1—1=2, так как в схеме имеется источник то­ка, ток которого может быть при­нят равным контурному току. За­дадимся произвольным направле­нием контурных токов I _k1 I _k2 как показано на рис. 6.

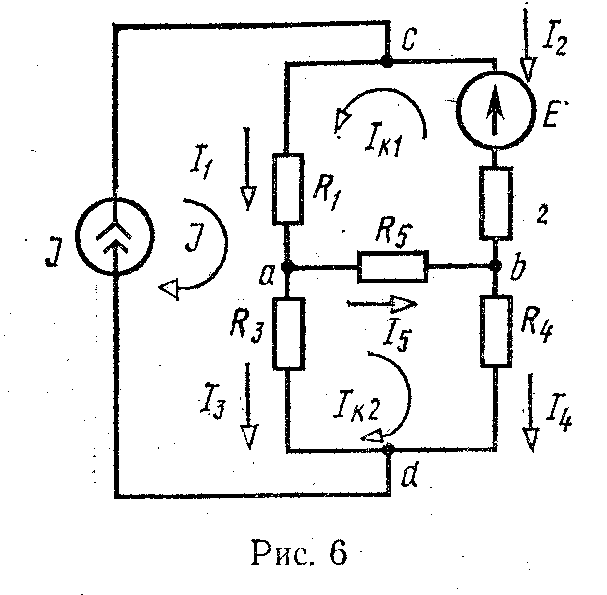
Там же нанесен известный контурный ток источника тока.

Составим систему уравнений первого и второго контуров:

Подставляя числовые значения и решая эти уравнения, найдем контурные токи:

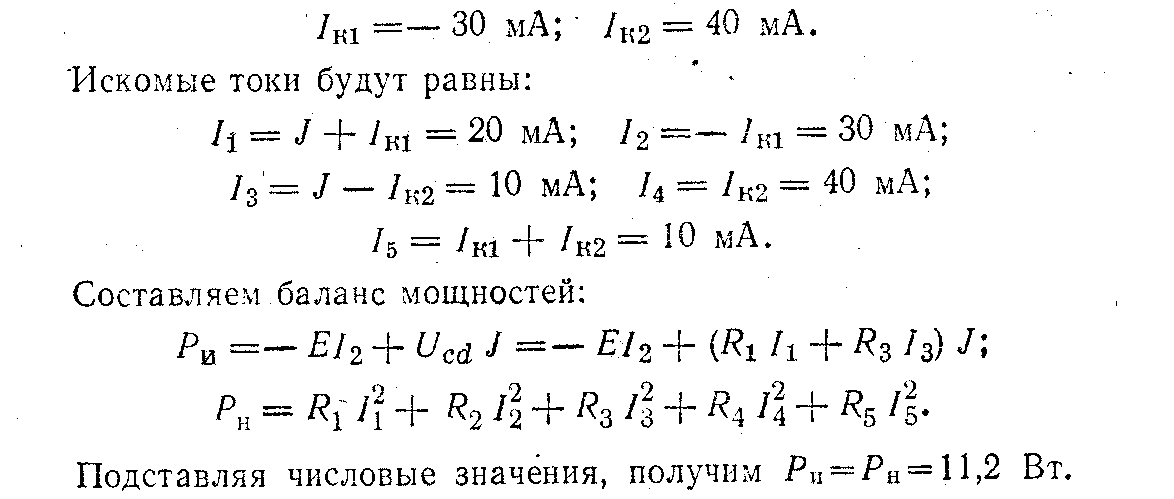
Метод наложения, основанный на принципе суперпозиции, по­зволяет свести расчет разветвленной цепи с несколькими источни­ками к нескольким расчетам этой же цепи, но с одним источником. Порядок расчета: 1) поочередно рассматривают действие в цепи только одного источника, а все остальные источники исключаются (остаются только их внутренние сопротивления); 2) рассчитывают токи в ветвях от действия каждого источника; 3) алгебраическим суммированием токов, полученных от действия каждого источника в отдельности, находят токи в ветвях цепи.

Метод является особенно эффективным при расчете токов, ког­да изменяется значение э. д. с. только одного источника.

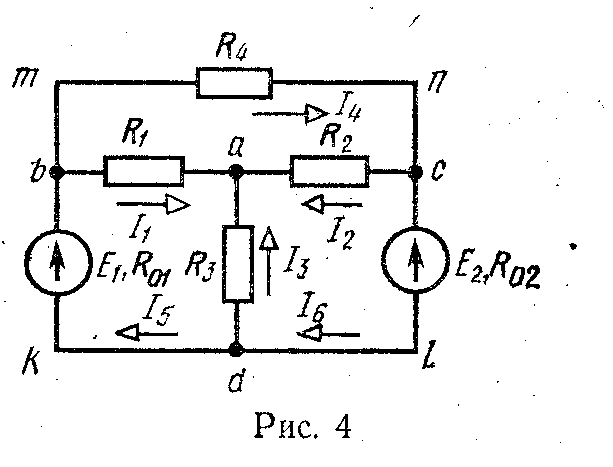
В промышленной электронике, автоматике часто используют цепи, схема которых изображена на рис. 7.

Такие схемы удобно анализировать с помощью метода узлового напряжения (напряже­ния между двумя узлами).

Задача. Найти токи и показание вольтметра в цепи, схема ко­торой приведена на рис. 7

R1=R2=R3=R4=10 Ом