Пошук мінімума кількох змінних
м-файл
function f= Fxy(x)
f=-x(1).*x(2).^2.*(1-x(1)-x(2));
протокол програми
>> [xmin, mif]=fminsearch(@ Fxy,[0;0])
Exiting: Maximum number of function evaluations has been exceeded
- increase MaxFunEvals option.
Current function value: -7326355666543599900000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000.000000
xmin =
1.0e+041 *
2.8668
-4.2691
mif =
-7.3264e+165
Формування графіків xy
Гра́фік — має загальне значення: наочне зображення кількісної залежності різних явищ, процесів тощо. Якщо простіше, то це є малюнок, на якому можна побачити як змінюється значення Y в залежності від значення Х. Як правило, значення X позначають на горизонтальній прямій, яку називають віссю абсцис (x), а значення Y на перпендикулярній до неї прямій, яку називають віссю ординат (y). Ці осі разом утворюють систему координат. Кожна вісь має напрямок, у якому значення відповідної координати зростає. У точці найбільшого значення малюють стрілку, яка вказує цей напрям. На кожній осі роблять позначки окремих (ключових) значень і підписують їх цими значеннями. Це допомагає приблизно визначити інші проміжні значення. Точка з координатами x=0 і y=0 називається початком координат.
>> %Задача 1
>> a=-pi;
>> b=pi;
>> h=pi./8;
>> x=a:h:b;
>> y=0.5.*x+cos(x).^2
y =
Columns 1 through 15
-0.5708 -0.5209 -0.6781 -0.8353 -0.7854 -0.4426 0.1073 0.6572 1.0000 1.0499 0.8927 0.7355 0.7854 1.1282 1.6781
Columns 16 through 17
2.2280 2.5708
>> z=sin(x).^2+cos(x)
z =
Columns 1 through 15
-1.0000 -0.7774 -0.2071 0.4709 1.0000 1.2362 1.2071 1.0703 1.0000 1.0703 1.2071 1.2362 1.0000 0.4709 -0.2071
Columns 16 through 17
-0.7774 -1.0000
>> plot(x,y,'-',x,z,'-.');
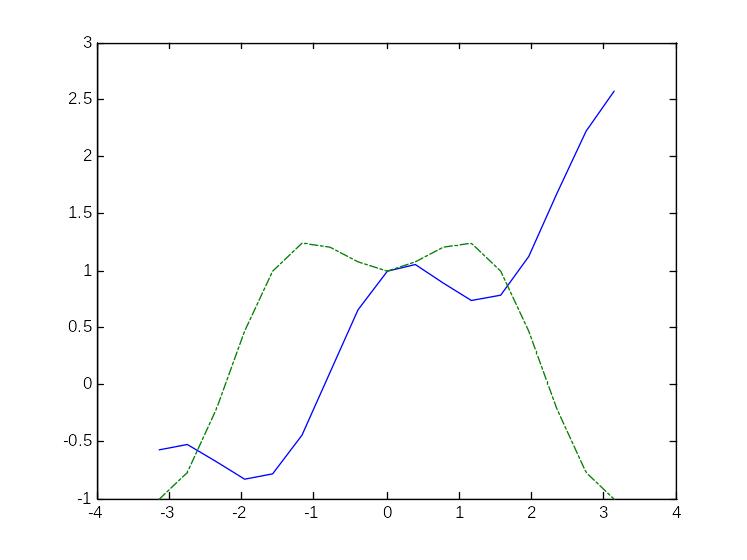
>> %Задача 2
>> a=-pi;
>> b=pi;
>> h=pi./8;
>> x=a:h:b;
>> y=0.5.*x+cos(x).^2
y =
Columns 1 through 15
-0.5708 -0.5209 -0.6781 -0.8353 -0.7854 -0.4426 0.1073 0.6572 1.0000 1.0499 0.8927 0.7355 0.7854 1.1282 1.6781
Columns 16 through 17
2.2280 2.5708
>> z=sin(x).^2+cos(x)
z =
Columns 1 through 15
-1.0000 -0.7774 -0.2071 0.4709 1.0000 1.2362 1.2071 1.0703 1.0000 1.0703 1.2071 1.2362 1.0000 0.4709 -0.2071
Columns 16 through 17
-0.7774 -1.0000
>> figure
>> subplot(2,1,1)
>> bar(x,y)
>> subplot(2,1,2)
>> bar(x,z)
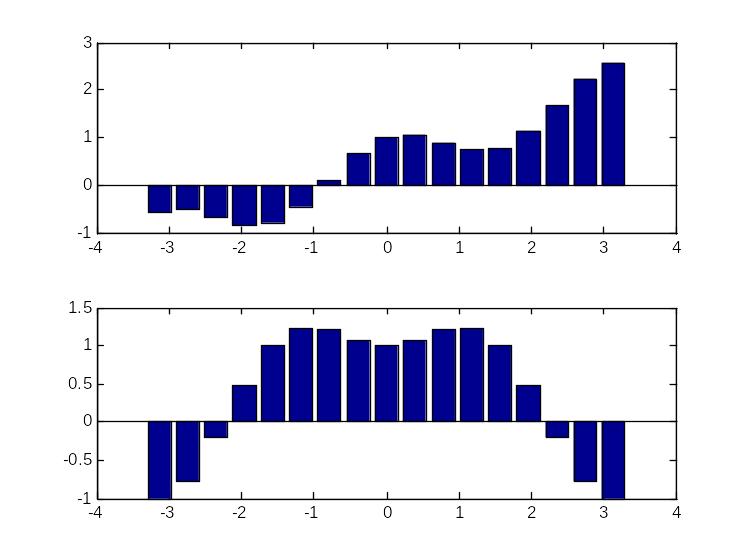
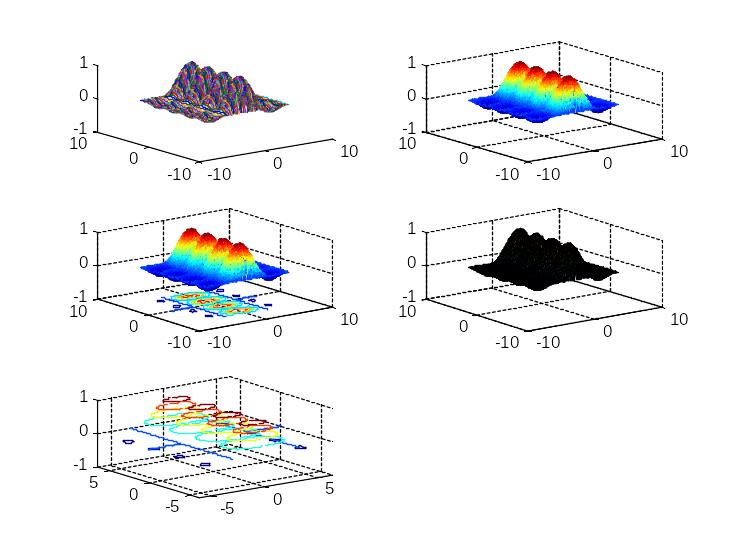
Формування об’ємних графіків
У різних вікнах
>> [ X, Y ] = meshgrid([ -2.*pi : pi/20 : 2.*pi ]);
>> Z=(sin(X)./X).*abs(sin(Y));
>> figure(1);
>> plot3(X,Y,Z);
>> figure(2);
>> mesh(X,Y,Z);
>> figure(3);
>> meshc(X,Y,Z);
>> figure(4);
>> surf(X,Y,Z);
>> figure(5);
>> contour(X,Y,Z);
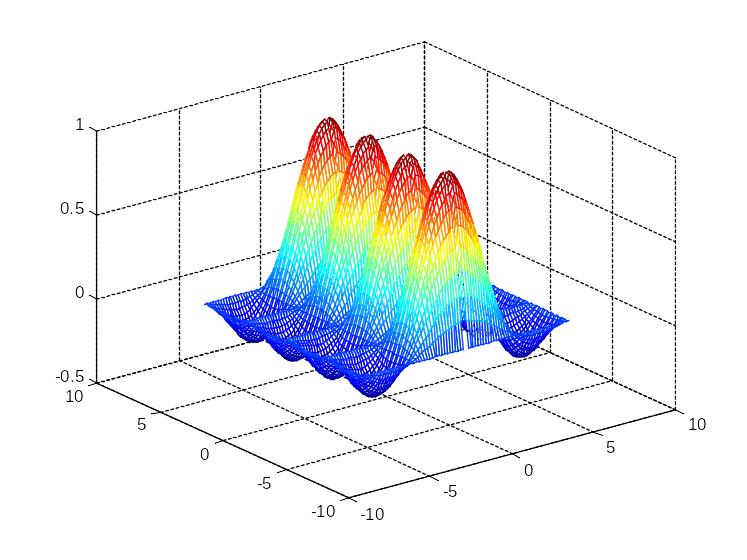
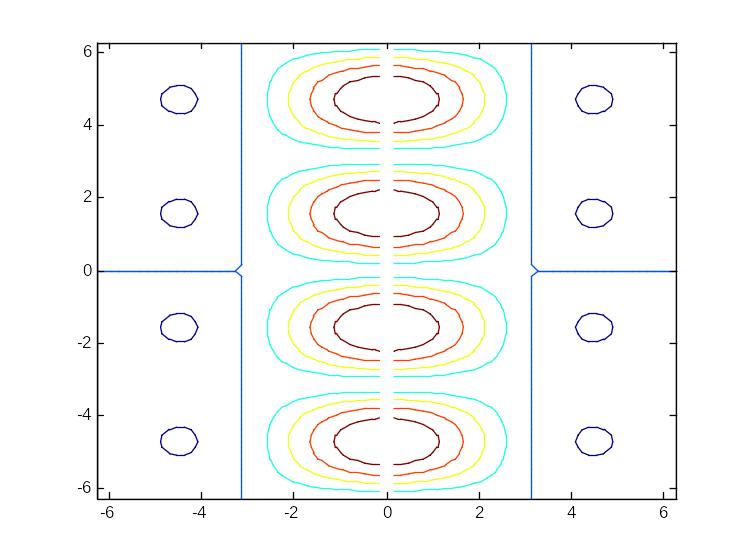
У одному вікні
>> [ X, Y ] = meshgrid([ -2.*pi : pi/20 : 2.*pi ]);
>> Z=(sin(X)./X).*abs(sin(Y));
>> figure
>> subplot(3,2,1)
>> plot3(X,Y,Z)
>> subplot(3,2,2)
>> mesh(X,Y,Z)
>> subplot(3,2,3)
>> meshc(X,Y,Z)
>> subplot(3,2,4)
>> surf(X,Y,Z)
>> subplot(3,2,5)
>> contour3(X,Y,Z)
Розв’язання рівнянь
Нелінійні рівняння
Алгебраїчним нелінійним рівнянням степеня n називається рівняння типу , де є многочленом степеня n, тобто, таке рівняння має такий вигляд: , де називають коефіцієнтами рівняння.
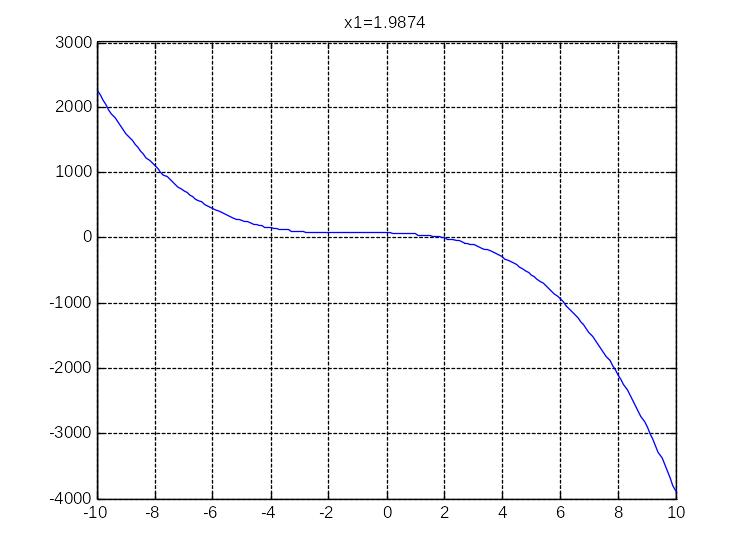
м-файл
function f1=fun1(x)
f1=-3*x.^3-9*x.^2-8*x+75;
протокол
>> Задача 1
>> x=-10:0.1:10;
>> plot(x,fun1(x));
>> grid on;
>> x1=fzero('fun1(x)',[1 2]);
>> result=strcat('x1=', num2str(x1))
title(result)
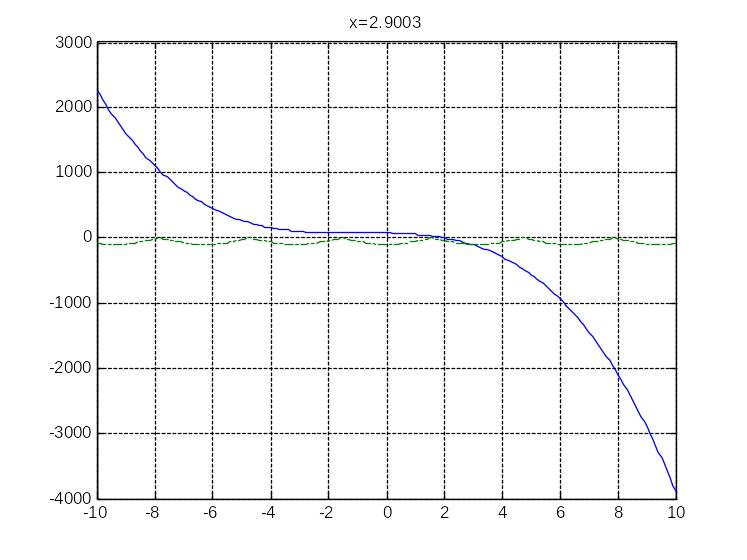
Система з 2 нелінійних рівнянь
>> % Задача 2
>> x=-10:0.1:10;
>> plot(x,fun1(x),'-',x,fun2(x),'-.');
>> x1=fzero('fun3(x)',[2 4]);
>> result=strcat('x=', num2str(x1));
>> title(result);
Символьні обчислення
Системи комп'ютерної алгебри забезпечуються спеціальним процесором для виконання аналітичних (символьних) обчислень. Його основою є ядро, щозберігає всю сукупність формул і формульних перетворень, за допомогоюяких робляться аналітичні обчислення. Чим більше цих формул у ядрі, тимбільш надійна робота символьного процесора і тем імовірніше, щопоставлена задача буде розв’язана , якщо такий розв’язок існує впринципі (що буває далеко не завжди).
>> %Задача 1
>> syms x
>> f1=(1+x).^5;
>> f1_exp=expand(f1)
f1_exp =
x^5 + 5*x^4 + 10*x^3 + 10*x^2 + 5*x + 1
>> f1_sim=simple(f1_exp)
f1_sim =
(x + 1)^5
>> %Порівяння
>> f1-f1_sim
ans =
0
>> %Задача 2
>> syms x
>> f1=(1+x).^5;
>> f1_dx=diff(f1,'x',1)
f1_dx =
5*(x + 1)^4
>> f1_it=int(f1_dx,'x')
f1_it =
(x + 1)^5
>> %Перевірка
>> f1-f1_it
ans =
0