Апроксимація функції
Апроксима́ція (лат. approximare — наближати) — наближене вираження одних математичних об'єктів іншими, простішими, наприклад, кривих ліній — ламаними, ірраціональних чисел — раціональними, неперервних функцій — многочленами.
Апроксимації присвячені окремі розділи сучасної математики, наприклад, діофантові наближення — апроксимація ірраціональних чисел раціональними, наближення та інтерполяція функцій — апроксимація неперервних функцій алгебраїчними і тригонометричними многочленами.
>> x=[ -4 -3 -2 -1 0 1 2];
>> y=[1.71 1.56 1.24 1.36 1.78 2.21 4.31];
>> plot(x, y, 'o')
Norm of residuals =
0.2987.
Диференційні рівняння
Диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.
Теорія диференціальних рівнянь — розділ математики, що займається вивченням диференціальних рівнянь і пов'язаних з ними задач. Їх результати застосовуються в багатьох природничих науках, особливо широко — у фізиці.
Простіше кажучи, диференціальне рівняння — це рівняння, в якому невідомою величиною є деяка функція. При цьому, в самому рівнянні бере участь не тільки невідома функція, але й різні її похідні. Диференціальним рівнянням описується зв'язок між невідомою функцією та її похідними. Такі зв'язки віднаходяться в різних областях знань: у механіці, фізиці, хімії, біології, економіці та ін.
м-файл
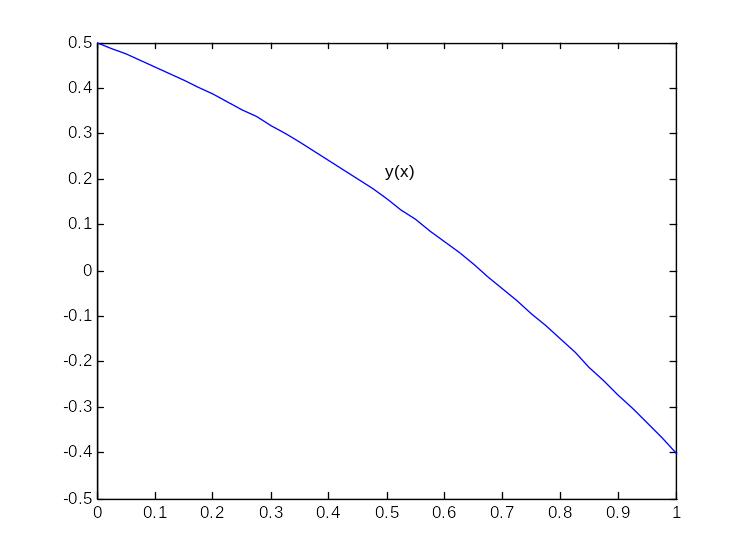
function dydx=F(x,y)
dydx=zeros(1,1);
dydx(1)=exp(-y)-exp(x)-0.1;
протокол програми
>> [X Y]=ode45( @ F,[0 1],0.5);
>> plot(X,Y);
>> hold on;
>> gtext('y(x)');
Численне обрахування визначених інтегралів
Визначений інтеграл — в математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральним функціям і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
Подальші узагальнення поняття дозволяють розширити його на кратні, поверхневі, об'ємні інтеграли, а також на інтеграли на об'єктах ширшої природи з мірою. Існує кілька різновидів визначених інтегралів: інтеграл Рімана, інтеграл Лебега, інтеграл Стілтьєса тощо.
Метод трапецій
>> x=0:0.001:5;
>> y=1./(sqrt(1+3.*x+2.*x.^2));
>> trapz(x,y)
ans =
1.4605
Метод Сімпсона
quad('1./(sqrt(1+3.*x+2.*x.^2))',0,5)
ans =
1.4605
Численне вирішування нелінійних рівнянь
Алгебраїчним
нелінійним рівнянням степеня n називається
рівняння типу
,
де
є многочленом степеня n, тобто, таке
рівняння має такий вигляд:
,
де
називають коефіцієнтами рівняння.
>> x=0:0.01:1;
>> y=x.^2-cos(x);
>> plot(x,y)
>> grid on
>> X1=fzero('x.^2-cos(x)',[0 1])
X1 =
0.8241
>> help fsolve
fsolve not found.
Численне вирішування оптимізаційних задач
Задачею оптимізації в математиці називається задача про знаходження екстремума (мінімума або максимума) дійсної функції у деякій області. Як правило, розглядаються області, що належать Rn і задані набором рівностей і нерівностей.
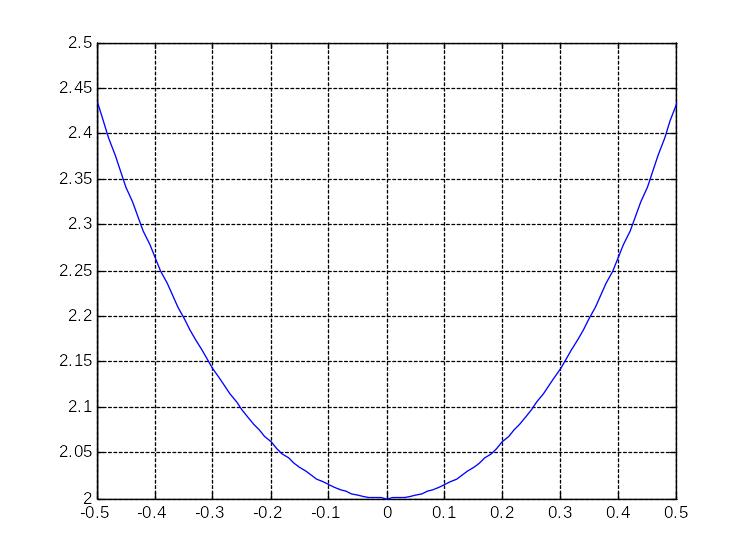
>> x=-0.5:0.01:0.5;
>> y=(((exp(x)+exp(-x))./2)).^3+1;
>> plot(x,y);
>> grid on;
>> [x y]=fminbnd('(((exp(x)+exp(-x))./2)).^3+1',-0.5,0.5)
x =
-5.5511e-017
y =
2
