МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

Факультет №3: Систем управления, информатики и электроэнергетики

Кафедра 308

Лабораторная работа №2

по курсу: «Теория и методы оптимизации»

на тему: «Алгоритмы прямого поиска в многомерной минимизации»

Выполнили: студенты группы 03-418

Пуршев Ю. Ю.

Гуров Р. В.

Проверил:

Исаева О. О.

Москва 2014

1/8. Анализ тестовых функций и построение линий уровня.

Для анализа тестовых функций составим системы уравнений из частных производных

и найдем стационарные точки: встака №1

Линии уровня исследуемых функций представлены на рисунках 1,2 и 3 (стр.3).

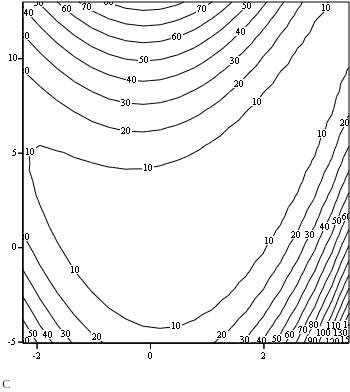
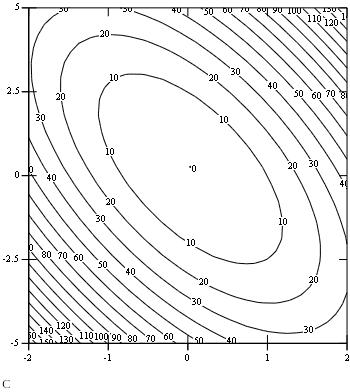
Рис. 1 - линии уровня функции f₁(x) Рис.2 - линии уровня функции f₂(x)

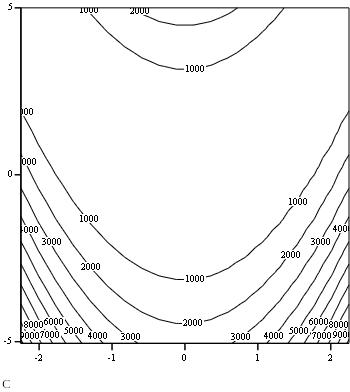
Рис.3 – линии уровня функции f₃(x)

2/8. Вычислительный эксперимент 1: минимизация методом s-квадрат и Нелдера-Мида.

Воспользуемся данными, полученными в пункте 1/8, и готовыми программами S2_q.exe, S2_r.exe, NLMD_q.exe, NLMD_r.exe, введя заданные исходные данные, заполним первые три столбца таблицы 1 (стр 4).

3/8. Программирование метода Хука-Дживса.

Для реализации вычислительного эксперимента 2, были разработаны алгоритмы программ HKDV_q и HKDV_r для квадратичной формы и функции Розенброка соответственно. Листинги программ приведены в приложении. Полученные результаты внесены в 4ый столбец таблицы 1 (стр4), тем самым завершая ее заполнение.

Разработав блок-схему, разработав, отладив и протестировав программу, провели вычислительный эксперимент 2, после чего заполнили четвертый столбец таблицы 1.

Заполненная в процессе выполнения предыдущих пунктов таблица расположена на странице 4.

4/8. Построение траекторий поиска минимума.

Используя результаты работы программ S2_q.exe, NLMD_q.exe и HKDV_q.exe построим траектории поиска минимума на фоне линий для трех методов и функции f₁(x), предварительно записав координаты 3 начальных итерации метода и конечной точки поиска.

Для метода S-квадрат: 1. (0,5; -2,8); 2. (1,11; -2,18); 3. (-0,758; -1,83); 4. (0,275;-1,96).

Для метода Нелдера-Мида: 1. (0,5; -2,8); 2. (1; -2,3); 3. (0,25; -1,3); 4. (-0.25; -1,3).

Для метода Хука-Дживса: 1. (0,5; -2,8); 2. (-0.5; -3.8); 3. (0;0); 4. (0.5; -2.6).

Полученный график представлен на рисунке 4., в котором на фоне линий уровня функции f₁(x) нанесены следующие линии: черной линией показаны итерации поиска методом S-квадрат; серой линией – методом Нелдера-Мида; прерывистой линией – методом Хука-Дживса. Также на рисунок 4 нанесены конечные точки поиска минимума. Точкой обозначены координаты точки минимума, достигнутой - методом S-квадрат; косым крестом - Хука-Дживса; прямым крестом - Нелдера-Мида.

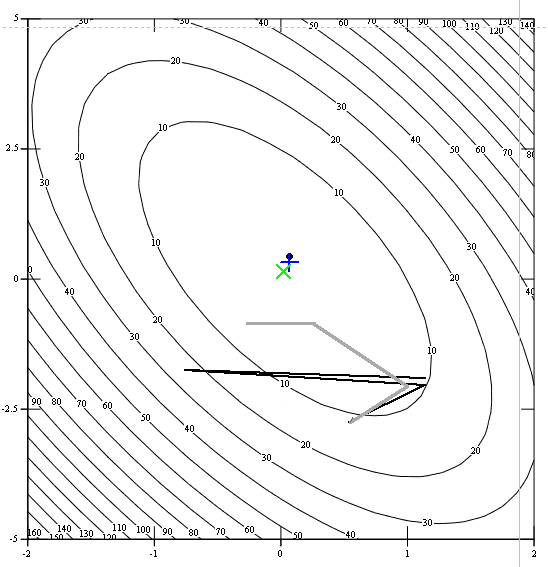
Рис.4. Итерации поиска различными методами.

Таблица 1. Результаты минимизации

Метод минимизации Целевая функция	Метод S-квадрат	Метод Нелдера-Мида	Метод Хука-Дживса
Квадратичная форма f1(x) = 12x12 + 6x1x2 + 2x22-2x1-x2 Точный минимум x* = (1/30, 1/5) Значение f в минимуме F(x*) = -0,133	1) Нач. точка x01 (0,5; -2,8)Т x** = (0,088021; -0,002407) f(x**) = -0,081922; Nвф = 77; 2) Нач. точка x02 (-2,7;0,5)Т x** = (0007394; 0.460476); f(x**) = -0,030104; Nвф = 109;	1) Нач. точка x01 (0,5; -2,8)Т x** = (-0.062012;0,25661) f(x**) = -0,050231; Nвф = 33; 2) Нач. точка x02 (-2,70,5)Т x** = (-0.0700; 0.4330); f(x**) = -0.041092; Nвф = 27;	1) Нач. точка x01 (0.5; -2.8)Т x**= (0.032999;0.199999) f(x**) = -0.133332; Nвф = 314; Нач. точка x02 (-2.7;0.5)Т x** = (0.032999; 0.199999); f(x**) = -0.133332; Nвф = 469;
Функция Розенброка f2(x) = 0.5(x2 - x12 )2 + (1 – x1)2; Точный минимум x* = (1,1) Значение f2 в минимуме f2(x*) = 0	1) Нач. точка x01=(-1.2, 1)T x** = (1.005388; 1.039895) f(x**) = 0.000452; Nвф = 56; 2)Нач. точка x02=(-0.6,-0.6)T x** = (0.986574; 0.964477); f(x**) = 0.000219; Nвф = 58;	1) Нач. точка x01=(-1.2, 1)T x** = (0.959546; 0.933014) f(x**) = 0.001712; Nвф = 50; 2)Нач. точка x02=(-0.6,-0.6)T x** = (1.016669; 1.027838) f(x**) = 0.000295; Nвф = 42;	1) Нач. точка x01=(-1.2, 1)T x** = (1.00000; 1.000000) f(x**) = 0.000000; Nвф = 135; 2)Нач. точка x02=(-0.6,-0.6)T x** = (1.009889; 1.028889) f(x**) = 0.000138; Nвф = 115;
Функция Розенброка f3(x) = 100(x2 - x12 )2 + (1 – x1)2; Точный минимум x* = (1,1) Значение f3 в минимуме f3(x*) = 0	1) Нач. точка x01=(-1.2, 1)T x** = (1.329854; 1.778881) f(x**) = 5.438972; Nвф = 67; 2)Нач. точка x02=(-0.6,-0.6)T x** = (0.457756; 0.206404); f(x**) = 0.295013; Nвф = 91;	1) Нач. точка x01=(-1.2, 1)T x** = (1.002233; 1.000244) f(x**) = 0.001792; Nвф = 161; 2)Нач. точка x02=(-0.6,-0.6)T x** = (0.985120; 0.966935); f(x**) = 0.001465; Nвф = 121;	1) Нач. точка x01=(-1.2, 1)T x** = (1.000009; 1.000019) f(x**) = 0.000000; Nвф = 841; 2)Нач. точка x02=(-0.6,-0.6)T x** = (0.999999; 0.999999); f(x**) = 0.000000; Nвф = 423;