2.2 Расчет показателей по выбранному алгоритму
Построим поле корреляции и сделаем вывод о зависимости показателей.
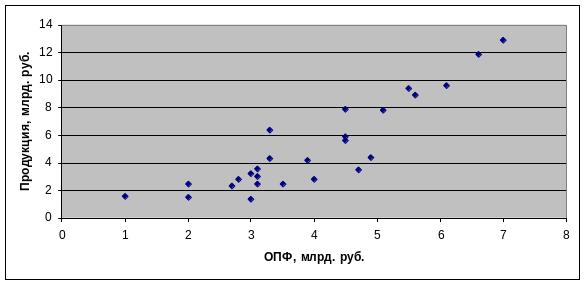
Рис. 1. Зависимость между стоимостью основных фондов и объемом продукции.
Между стоимостью ОПФ и выпуском продукции существует тесная прямая взаимосвязь.
Определим число интервалов по формуле Стерджесса: k = 1 + 3,322lgN, где N – число показателей.
Таким образом, k = 1 + 3,322lg26 ≈ 5,7 = 6 групп.
Основные
производственные фонды:
млрд. руб. (включаем в группу по верхней
границе).
Объем продукции
в сопоставимых ценах:
млрд. руб.
Обозначим границы групп и подсчитаем число предприятий в каждой группе.
Таблица 2.1
Интервалы группировок.
Группа |
Стоимость ОПФ, млрд. руб. |
Объем продукции, млрд. руб. |
||
Интервал |
Число предприятий |
Интервал |
Число предприятий |
|
1 |
1 – 2 |
3 |
1,400 – 3,317 |
11 |
2 |
2 – 3 |
4 |
3,317 – 5,233 |
5 |
3 |
3 – 4 |
8 |
5,233 – 7,150 |
3 |
4 |
4 – 5 |
5 |
7,150 – 9,067 |
3 |
5 |
5 – 6 |
3 |
9,067 – 10,983 |
2 |
6 |
6 – 7 |
3 |
10,983 – 12,900 |
2 |
Таблица 2.2
Таблица для расчета средней величины и дисперсии.
№ |
Группы предприятий по ОПФ, млн. руб. |
|
f |
|
|
|
|
А |
Б |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
1 – 2 |
1,5 |
3 |
4,5 |
-2,38 |
5,6864 |
17,0592 |
2 |
2 – 3 |
2,5 |
4 |
10 |
-1,38 |
1,9172 |
7,6686 |
3 |
3 – 4 |
3,5 |
8 |
28 |
-0,38 |
0,1479 |
1,1834 |
4 |
4 – 5 |
4,5 |
5 |
22,5 |
0,62 |
0,3787 |
1,8935 |
5 |
5 – 6 |
5,5 |
3 |
16,5 |
1,62 |
2,6095 |
7,8284 |
6 |
6 – 7 |
6,5 |
3 |
19,5 |
2,62 |
6,8402 |
20,5207 |
Всего по совокупности: |
26 |
101 |
|
|
56,1538 |
||
Мода:
млрд. руб.
Медиана:
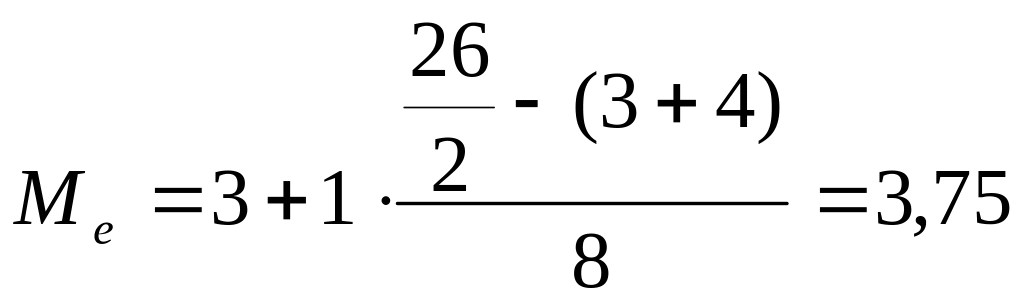млрд. руб.
Средний объем
продукции составляет
млрд. руб.
Дисперсия:
Среднее квадратическое
отклонение:
Коэффициент
вариации:
.
Средняя стоимость основных производственных фондов по структурированным данным составляет 3,88 млрд. руб.
У большинства кварталов средняя стоимость ОПФ 3,57 млрд. руб. В половине кварталов среднегодовая стоимость основных производственных фондов не превышает 3,75 млрд. руб.
Коэффициент вариации показывает, что 37,83% всей совокупности находятся под влиянием стоимости ОПФ, а на остальные 62,17% совокупности влияют другие факторы. Так как коэффициент вариации больше 33%, то можно сказать, что совокупность по своему составу неоднородна.
Следующим этапом заполняем корреляционную таблицу.
Корреляционная решетка представляет собой комбинационную таблицу, в подлежащем которой располагаются значения факторного признака, а в сказуемом – результативного признака. В клетках, образовавшихся при пересечении строк и столбцов, указываются частоты, т.е. число случаев, в которых одни значения сочетаются с другими.
Таблица 2.3
Зависимость объема продукции от стоимости ОПФ
Группа предприятий по стоимости ОПФ, Х |
Группы предприятий по объему продукции, Y |
Итого: |
|||||
1,40 – 3,32 |
3,32 – 5,23 |
5,23 – 7,15 |
7,15 – 9,07 |
9,07 – 10,98 |
10,98 – 12,90 |
||
1 – 2 |
3 |
– |
– |
– |
– |
– |
3 |
2 – 3 |
4 |
– |
– |
– |
– |
– |
4 |
3 – 4 |
4 |
3 |
1 |
– |
– |
– |
8 |
4 – 5 |
– |
2 |
2 |
1 |
– |
– |
5 |
5 – 6 |
– |
– |
– |
2 |
1 |
– |
3 |
6 – 7 |
– |
– |
– |
– |
1 |
2 |
3 |
Итого: |
11 |
5 |
3 |
3 |
2 |
2 |
26 |
По корреляционной таблице можно сделать вывод о форме и направлении связи, о степени тесноты связи. Так как сосредоточение частот около диагонали таблицы идет с левого верхнего угла в правый нижний, то можно сказать, что связь между показателями прямая и тесная. Об этом свидетельствует плотность концентрации частот.
Прямолинейной называется связь, когда величина явления изменяется приблизительно равномерно в соответствии с изменением величины влияющего фактора. Математически прямолинейная связь может быть выражена уравнением прямой: , коэффициенты которой находятся по формулам: , .
Параметр а1 называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признака х на одну единицу.
Таблица 2.4
Расчет параметров коэффициентов регрессии
№ |
ОПФ |
Q |
|
|
|
|
|
E |
Ε2 |
1 |
1,0 |
1,6 |
1,00 |
1,60 |
8,725 |
12,196 |
-0,808 |
2,408 |
5,800 |
2 |
2,0 |
2,5 |
4,00 |
5,00 |
3,818 |
6,720 |
1,189 |
1,311 |
1,718 |
3 |
2,0 |
1,5 |
4,00 |
3,00 |
3,818 |
12,905 |
1,189 |
0,311 |
0,097 |
4 |
2,7 |
2,3 |
7,29 |
6,21 |
1,572 |
7,797 |
2,588 |
-0,288 |
0,083 |
5 |
2,8 |
2,8 |
7,84 |
7,84 |
1,331 |
5,255 |
2,787 |
0,013 |
0,000 |
6 |
3,0 |
1,4 |
9,00 |
4,20 |
0,910 |
13,633 |
3,187 |
-1,787 |
3,193 |
7 |
3,0 |
3,2 |
9,00 |
9,60 |
0,910 |
3,581 |
3,187 |
0,013 |
0,000 |
8 |
3,1 |
3,0 |
9,61 |
9,30 |
0,729 |
4,378 |
3,387 |
-0,387 |
0,149 |
9 |
3,1 |
2,5 |
9,61 |
7,75 |
0,729 |
6,720 |
3,387 |
-0,887 |
0,786 |
10 |
3,1 |
3,6 |
9,61 |
11,16 |
0,729 |
2,227 |
3,387 |
0,213 |
0,046 |
11 |
3,3 |
6,4 |
10,89 |
21,12 |
0,428 |
1,710 |
3,786 |
2,614 |
6,832 |
12 |
3,3 |
4,3 |
10,89 |
14,19 |
0,428 |
0,628 |
3,786 |
0,514 |
0,264 |
13 |
3,5 |
2,5 |
12,25 |
8,75 |
0,206 |
6,720 |
4,186 |
-1,686 |
2,842 |
14 |
3,9 |
4,2 |
15,21 |
16,38 |
0,003 |
0,796 |
4,985 |
-0,785 |
0,616 |
15 |
4,0 |
2,8 |
16,00 |
11,20 |
0,002 |
5,255 |
5,185 |
-2,385 |
5,686 |
16 |
4,5 |
7,9 |
20,25 |
35,55 |
0,298 |
7,883 |
6,183 |
1,717 |
2,947 |
17 |
4,5 |
5,6 |
20,25 |
25,20 |
0,298 |
0,258 |
6,183 |
-0,583 |
0,340 |
18 |
4,5 |
5,9 |
20,25 |
26,55 |
0,298 |
0,652 |
6,183 |
-0,283 |
0,080 |
19 |
4,7 |
3,5 |
22,09 |
16,45 |
0,557 |
2,535 |
6,583 |
-3,083 |
9,504 |
20 |
4,9 |
4,4 |
24,01 |
21,56 |
0,895 |
0,479 |
6,982 |
-2,582 |
6,669 |
21 |
5,1 |
7,8 |
26,01 |
39,78 |
1,314 |
7,332 |
7,382 |
0,418 |
0,175 |
22 |
5,5 |
9,4 |
30,25 |
51,70 |
2,391 |
18,556 |
8,181 |
1,219 |
1,486 |
23 |
5,6 |
8,9 |
31,36 |
49,84 |
2,710 |
14,499 |
8,381 |
0,519 |
0,270 |
24 |
6,1 |
9,6 |
37,21 |
58,56 |
4,606 |
20,319 |
9,380 |
0,220 |
0,049 |
25 |
6,6 |
11,9 |
43,56 |
78,54 |
7,002 |
46,345 |
10,378 |
1,522 |
2,316 |
26 |
7,0 |
12,9 |
49,00 |
90,30 |
9,279 |
60,960 |
11,177 |
1,723 |
2,967 |
Итого: |
102,8 |
132,4 |
460,4 |
631,33 |
53,985 |
270,338 |
|
0,000 |
54,914 |
Средняя: |
3,95 |
5,09 |
17,71 |
24,28 |
|
|
|
|
|
Следовательно,
уравнение регрессии:
Для измерения тесноты связи используется коэффициент корреляции.
Коэффициент корреляции принимает значения от – 1 до +1, причем если rxy > 0, то корреляция прямая, если rxy < 0, то корреляция обратная, а если rxy = 0, то связь отсутствует полностью.
В зависимости от того, насколько rxy приближается к ±1, различают связь слабую, умеренную, заметную, высокую, тесную и очень тесную.
Таким
образом,
Тогда
.
Линейный коэффициент корреляции, равный 0,893, показывает, что между выпуском продукции в сопоставимых ценах и стоимостью основных производственных фондов существует очень тесная линейная связь.
Коэффициент
детерминации:
Коэффициент детерминации является конкретным показателем, т.к. он отвечает на вопрос о том, какая доля в общем результате зависит от фактора, положенного в основание группировки. Таким образом, на долю основных производственных фондов предприятия приходится 80% всех факторов, а остальная часть (20%) – это прочие неучтённые факторы.
С надежностью 0,95 проверим значимость оценок α0 и α1 теоретических коэффициентов регрессии а0 и а1 с помощью t – статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для уровня значимости
= 0,05 и числа степеней свободы к = n
– 2 = 26 – 2 = 24 критерий Стьюдента равен
Дисперсии, средние квадратичные отклонения коэффициентов a0 и a1 уравнения регрессии определим из равенств с использованием результатов таблицы 2.4
Для определения математической значимости коэффициентов a0 и a1 найдем t – статистику Стьюдента:
;
Сравнение расчетных
и табличных величин критерия Стьюдента
показывает, что
(–
3,24 < 2,064), а
(19,21 > 2,064), т.е. с надежностью 0,95 можно
сказать, что оценка a0
теоретического коэффициента α0
незначима, а оценка а1
– значима.
С надежностью 0,95 определим интервальные оценки теоретических коэффициентов α0 и α1 регрессии.
Подставив числовые значения, значения коэффициентов а0 и а1, их средние квадратичные отклонения и значение для t имеем:
– 2,806 – 2,064 × 0,8684 ≤ α0 ≤ – 2,806 + 2,064 × 0,8684 или
– 4,59 ≤ α0 ≤ – 1,02
Отрицательные по знаку значения верхней и нижней границ измерений коэффициента а0 свидетельствуют об его статистической значимости.
1,9976 – 2,064 × 0,2059 ≤ α1 ≤ 1,9976 – 2,064 × 0,2059 или 1,57 ≤ α0 ≤ 2,42
Одинаковые значения нижней и верхней границ измерений коэффициента а1 косвенно свидетельствует об его статистической незначимости.
Проверим при уровне значимости 0,05 значимость уравнения регрессии с помощью F статистики Фишера и сделаем соответствующие выводы о значимости уравнения регрессии.
Имеем
Найдем для заданной доверительной вероятности 0,05 критическое значение статистики Фишера: Fкр (α, 1, n – 2) = 4,260.
Имеем F > Fкр (т.е. 94,15 > 4,260), поэтому уравнение значимо с надежностью 0,95.
Заключение
Основные фонды предприятия предопределяют экономический потенциал страны. От их величины, качества и эффективности использования зависят масштабы и темпы роста национального богатства, повышения материального уровня жизни народа и улучшений условий труда.
Основными фондами являются материальные ценности, функционирующие в течение длительного периода времени. К ним относятся здания, сооружения, передаточные устройства, машины и оборудование, транспортные средства и т.д.
Основные фонды подразделяются на производственные и непроизводственные в зависимости от их участия в процессе производства. Основными производственными фондами называются те средства производства, которые в течение многих производственных циклов сохраняют свою натуральную форму и переносят свою стоимость на готовый продукт постепенно, в меру износа.
Во второй части контрольной работы был рассчитан алгоритм, представленный в пункте 1.3 контрольной работы. Анализ основных производственных фондов был рассчитан по ОАО «Трубодеталь» за период 2007 – 2013 гг.
Средняя стоимость основных производственных фондов по структурированным данным составляет 3,88 млрд. руб.
У большинства кварталов средняя стоимость ОПФ 3,57 млрд. руб. В половине кварталов среднегодовая стоимость основных производственных фондов не превышает 3,75 млрд. руб.
Коэффициент вариации показывает, что 37,83% всей совокупности находятся под влиянием стоимости ОПФ, а на остальные 62,17% совокупности влияют другие факторы. Так как коэффициент вариации больше 33%, то можно сказать, что совокупность по своему составу неоднородна.
Зависимость объема выручки от среднегодовой стоимости основных производственных фондов можно выразить уравнением регрессии:
Линейный коэффициент корреляции, равный 0,893, показывает, что между выпуском продукции в сопоставимых ценах и стоимостью основных производственных фондов существует очень тесная линейная связь.
На долю основных производственных фондов предприятия приходится 80% всех факторов, а остальная часть (20%) – это прочие неучтённые факторы. Сравнение расчетных и табличных величин критерия Стьюдента показывает, что (– 3,24 < 2,064), а (19,21 > 2,064), т.е. с надежностью 0,95 можно сказать, что оценка a0 теоретического коэффициента α0 незначима, а оценка а1 – значима.
Уравнение значимо с надежностью 0,95.
Список литературы
1. Баев И.А., Варламова З.Н., Васильева О.Е. и др. Экономика предприятия. Учебник для вузов. 4-е изд. / Под ред. акад. В.М. Семенова. - СПб: Питер, 2006.
2. Годин А.М. Статистика: Учебник. – 2-е изд., перераб. – М.: Издательско-торговая корпорация «Дашков и Ко», 2006. – 472 с.
3. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. М.: ИНФРА-М, 2007. – 416 с.
4. Ковалев А.П. Оценка стоимости активной части основных фондов. Учебно-методическое пособие - М.: Финстатинформ, 2003.
5. Практикум по теории статистики / Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 2007. – 394 с.
6. Практикум по социально-экономической статистике: Учебно-практическое пособие / Сост. Л.С. Салыева; УрСЭИ АТиСО. – Челябинск, 2005. – 128 с.
7. Сергеев И.В. Экономика предприятия. Учеб. пособие. - М: Финансы и статистика, 2000.
8. Румянцева Е.Е. Новая экономическая энциклопедия. - М: ИНФА-М, 2005.
9. Экономика предприятия. 100 экзаменационных ответов. Под ред. проф. А.С. Пелиха. - Ростов н/Д.: Издательский центр «МарТ», 2000.
10. Экономика предприятия. Учебник для ВУЗов /под ред. Грузинова В.П./ - М.: ЮНИТИ, 2001.
11. www. трубодеталь.рф
Приложение 1
Статистическая информация о результатах производственной деятельности организации, млн. руб.
Квартал |
№ |
Выпуск продукции |
Среднегодовая стоимость ОПФ |
3 кв. 2007 |
1 |
2,5 |
3,5 |
4 кв. 2007 |
2 |
2,8 |
4,0 |
1 кв. 2008 |
3 |
1,6 |
1,0 |
2 кв. 2008 |
4 |
12,9 |
7,0 |
3 кв. 2008 |
5 |
1,4 |
3,0 |
4 кв. 2008 |
6 |
3,0 |
3,1 |
1 кв. 2009 |
7 |
2,5 |
3,1 |
2 кв. 2009 |
8 |
7,9 |
4,5 |
3 кв. 2009 |
9 |
3,6 |
3,1 |
4 кв. 2009 |
10 |
8,9 |
5,6 |
1 кв. 2010 |
11 |
5,6 |
4,5 |
2 кв. 2010 |
12 |
4,4 |
4,9 |
3 кв. 2010 |
13 |
2,8 |
2,8 |
4 кв. 2010 |
14 |
9,4 |
5,5 |
1 кв. 2011 |
15 |
11,9 |
6,6 |
2 кв. 2011 |
16 |
2,5 |
2,0 |
3 кв. 2011 |
17 |
3,5 |
4,7 |
4 кв. 2011 |
18 |
2,3 |
2,7 |
1 кв. 2012 |
19 |
3,2 |
3,0 |
2 кв. 2012 |
20 |
9,6 |
6,1 |
3 кв. 2012 |
21 |
1,5 |
2,0 |
4 кв. 2012 |
22 |
4,2 |
3,9 |
1 кв. 2013 |
23 |
6,4 |
3,3 |
2 кв. 2013 |
24 |
4,3 |
3,3 |
3 кв. 2013 |
25 |
5,9 |
4,5 |
4 кв. 2013 |
26 |
7,8 |
5,1 |