1.2. Types of loads and deformations

In the process of work structural and machine elements are subjected to external load actions which can be subdivided into:

• triaxial loads (they are distributed in the body volume, for example, own weights, inertness, magnetic field forces);

• concentrated loads (those acting on a very small area);

• distributed loads (distributed on the body surface);

• static loads (the ones that increase slowly, conserve a maximum value in a long period of time and decrease slowly);

• dynamic loads (those changing quickly on the value).

The external loads cause the change of the body dimensions and shapes i.e. bodies are deformed. The basic deformation types are as follows:

• tension (dimensions increase in the action force direction);

• compression (dimensions decrease under the force action);

• shear (it is caused by the mutual displacement of the body parts which made up one whole in the opposite directions in one plane; it arises under cutting, stamping details from a sheet, while cutting by mechanical scissors);

• torsion (it arises under loading by twisting moments which have the action plane perpendicular to the bar axis and the mutual turn of the cross section in this section plane);

• bend (the bar axis turns into a curve and changes its curvature).

The external loads can cause two or three basic deformation types simultaneously.

1.3. Determining the internal forces by the method of sections. Stresses

The method of sections consists in that a body is cut by an imagining plane into two parts, one part is removed, and internal forces acting before the cutting are applied to the section of the remained part; the remaining portion of the body is considered as a separate body being in equilibrium under the external and internal forces applied to this section.

The method of sections is based on Newton^’s third law.

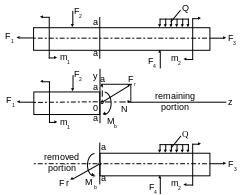
Fig. 1.1.

We can find the resultant of these forces by applying the equilibrium condition to the remaining body portion.

The bar is the basic calculating object in the strength of materials. Let us consider the static resultant of the internal forces in a bar cross section. Cut a bar by the cross section a-a and consider the equilibrium of its left portion (Fig.1.1).

The resultant force vector F_r applied in the centroid of the area and the resultant moment M_r = M_b (they balance the external force plane system applied to the remaining beam portion) are the static resultants of internal forces in the general case which act at the section a-a, if the external forces, applied to the bar, are in one plane.

Let us decompose the resultant force vector into the component N directed along the bar axis and the component Q perpendicular to this axis i.e. the axis lying at the cross-section plane.

These components of the resultant force vector and the resultant moment are called internal forces factors acting at a cross section of a bar. The component N is called the axial force, the component Q is called the shearing force and the couple forces with M_b are the bending moment.

Statics gives three eguations for the remaining bar portion to determine three pointed internal forces, namely:

(Z – is the axis always directed along the bar).

If the external forces acting at the bar do not lie in the same plane i.e. they form the spatial force system, then in the general case there arise six internal forces factors in the cross section. To determine these statics gives six equilibrium equations (Fig.1.2):

Fig. 1.2.

The six internal forces factors arising at the bar cross section in a most general case are given the following names: N is an axial force; Q_x, Q_y are shearing forces; M_t is a twisting moment; M_bx, M_by are bending moments.

There arise different internal forces factors at the bar cross section under different deformations. Consider the following special cases:

1. There is only an axial force N at the section. In this case we have a tension deformation (if the force is directed from the section) or a compression deformation (if the force is directed to the section).

2. There is only a shearing force Q, in this case we have a shear deformation.

3. There is only a twisting moment M_t. In this case we have a torsional deformation.

4. There is only a bending moment M_b. In this case we have a pure bending deformation. When a section has a simultaneous bending moment M_b and a simultaneous shearing force Q, the bend is called cross-bending.

5. When a section has some internal forces factors simultaneously (for example, a bending and a twisting moments or a bending moment and an axial force), then there is a combination of the basic deformations (combined stress).

The stress is one of basic concepts of the strength of materials.

The stress characterizes the intensity of internal forces acting over the section i.e. the load per a unit area.

Let us consider any arbitrary loading beam and apply to it the method of sections (Fig.1.3)

Let us remove from the section an infinitely small element of the area dA. Because the element is small, it can be assumed that within its limits the internal forces applied in different points are equal to the value and direction, hence, they form a system of parallel forces. The resultant of this system is denoted by dF. After dividing dF into the element area dA we can determine the internal forces intensity i.e. the stress p at the points of the element area dA and we get _adm

Thus, the stress is the internal force acting over a unit area of the section. The stress is the vector value.

The stress unit is:

Newton per square meter = = Pascal (Pa).

Fig.1.3.

Since this stress unit is very small, we shall apply a bigger divisible unit, namely megapascal (MPa):

1 MPa =10 ⁶ Pа = 1 N/mm².

Let us decompose the stress vector P into two components: - perpendicular to the section plane and -lying at the section plane (see Fig.1.3). These components are called as follows: is the normal stress,  is the shearing stress.

Since the angle between the normal and shearing stress is always 90⁰, then the absolute value of the resultant stress p is determined by the formula