Контрольные вопросы

1. Что такое продольный изгиб?

2. Какую величину сжимающей силы называют критической?

3. По какой формуле можно определить величину критической силы?

4. Укажите область применения формулы Эйлера.

5. Как влияет характер закрепления концов стержня на величину критической силы?

6. Укажите формулу для вычисления гибкости стержня.

7. Что называется предельной гибкостью стержня?

8. Какие характеристики материала необходимо знать для вычисления предельной гибкости стержня?

9. Какое практическое значение имеет определение критической силы сжатых стержней?

10. Зависит ли величина критической силы от упругих свойств материала стержня?

11. Во сколько раз изменится величина критической силы, если при испытании заменить шарнирные опоры стержня на опоры с жестким защемлением?

12. Сущность метода наименьших квадратов.

Литература

1. Федосьев В.И. Сопротивление материалов. - М.: Наука, 1986.-512с.

2. Тимошенко С.И. Устойчивость упругих систем. - М.: Гостехиздат,1995. -568с.

3. Леденко Л.Г. Керженцев В.В. Математическая обработка в оформление результатов эксперимента. -М.: Изд.МГУ, 1997. -112с.

4. Рубашин А.Г. Лабораторные работы по сопротивлению материалов. - М.: Высшая школа, 1971. -240с.

Лабораторная работа № 3

«Испытание на усталость при чистом изгибе»

Введение

Многие детали машин и элементы конструкций сооружений в процессе эксплуатации подвергаются действию нагрузок, меняющихся во времени. Если уровень напряжений превышает определенный, то в материале происходит накопление повреждений, приводящих к образованию трещин и последующему разрушению.

Разрушение в этом случае происходит при напряжениях значительно меньших, чем при статическом воздействии.

Процесс постепенного накопления повреждений в материале под действием переменных напряжений, приводящих к образованию трещины и разрушению, называется усталостью материала. Свойство материала противостоять усталости называется выносливостью.

Различают многоцикловую и малоцикловую усталости.

Многоцикловая усталость - усталость металла, при которой образование макротрещин или полное разрушение происходит от 5·10⁴ циклов и более.

Малоцикловая усталость - усталость металла, при которой образование макротрещин или полное разрушение происходит в упруго-пластической области до 5·10⁴ циклов.

Деление на многоцикловую и малоцикповую усталости условно.

Для расчета на усталостную прочность необходим целый ряд характеристик предельных состояний. Одной из них является предел усталости или предел выносливости.

Пределом выносливости называется наибольшее напряжение, при котором образец не разрушается до базы испытаний.

Для стальных образцов в обычных условиях база испытания равна 10⁷ циклов, для цветных металлов и высокопрочных сталей 10⁸ циклов.

Предел выносливости определяют экспериментально.

Схему нагружения образцов выбирают так, чтобы воспроизвести напряженное состояние аналогичное эксплуатационным условиям работы детали.

К основным типам нагружения относятся:

а) чистый изгиб при вращении;

б) то же в одной плоскости;

в) поперечный изгиб при вращении консольных круглых образцов;

г) то же в одной плоскости круглых и некруглых образцов;

д) поперечный изгиб консольных круглых и некруглых образцов. Испытания также проводят при комбинировании видов нагружения.

Теория

Характерной чертой усталостного разрушения является локализованность пластических деформаций вблизи трещины разрушения даже в случаях, когда деталь или образец изготовлены из такого материала, что в аналогичных условиях статического нагружения разрушению предшествует значительная пластическая деформация. Например, при растяжении цилиндрического образца из мягкой стали разрушение наступает после пластической деформации во всей рабочей части, достигающей 20 - 30 %, тогда как при знакопеременном продольном нагружении такого же образца усталостное разрушение происходит без заметной пластической деформации и только по характеру поверхностной трещины и по структуре материала вблизи ее можно установить, что в некоторой малой области в окрестности трещины имела место пластическая деформация.

Внешний вид излома состоит из двух зон: зоны постепенного развития трещины и зоны заключительного разрушения.

Зона постепенного развития трещины имеет матовую заглаженную поверхность, т.к. под влиянием многократно повторяющегося нагружения края трещины то расходятся, то сходятся, благодаря чему происходит заглаживание трещины. Зона заключительного разрушения имеет кристаллический вид вследствие разрушения отрывом.

Усталостная прочность материалов зависит не только от вида напряженного состояния, но и от характера изменения напряжений во времени.

Циклом напряжений называют однократную их смену, соответствующую полному периоду Т изменения.

Характер изменения напряжений во времени может быть самым различным. На рис.1 показаны наиболее простые изменения синусоидального типа.

г)

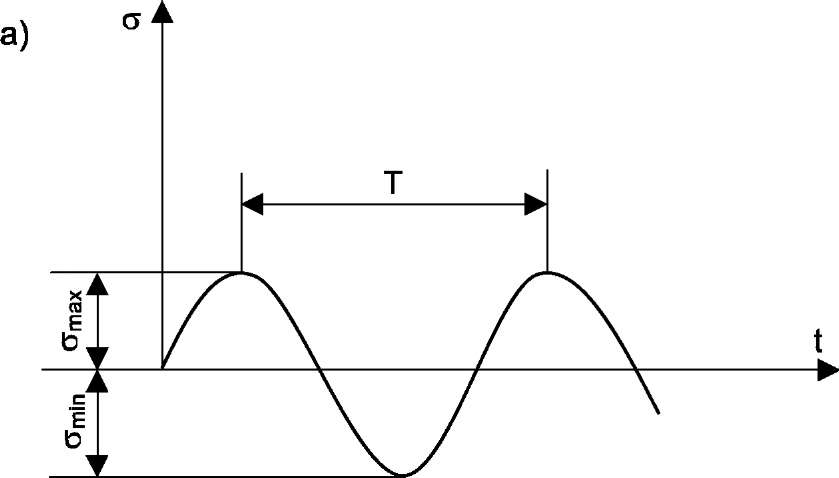
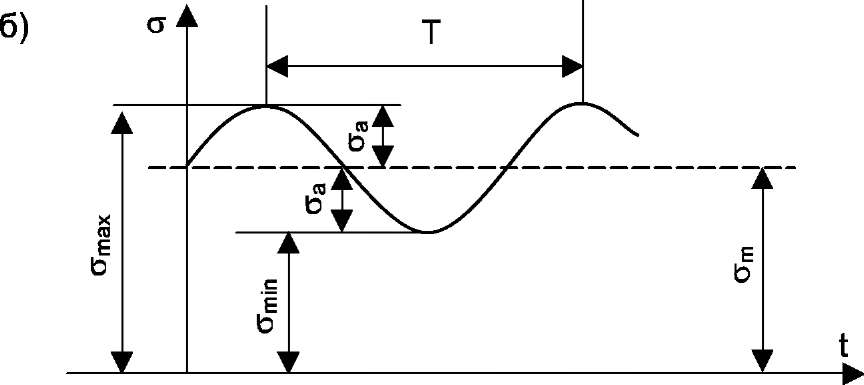
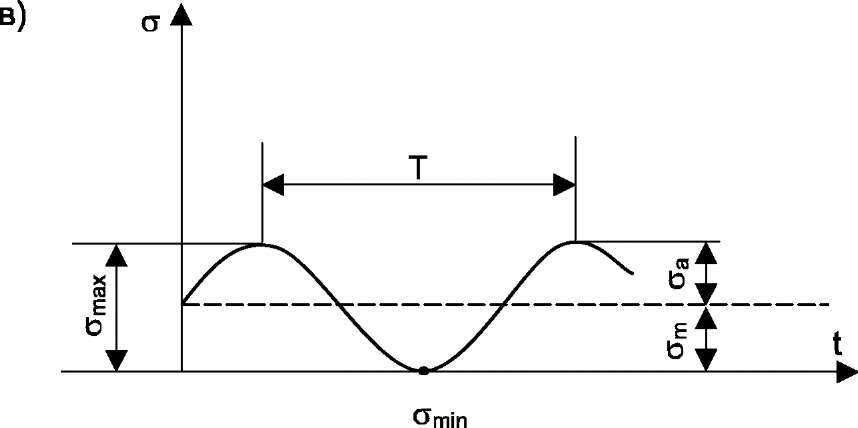
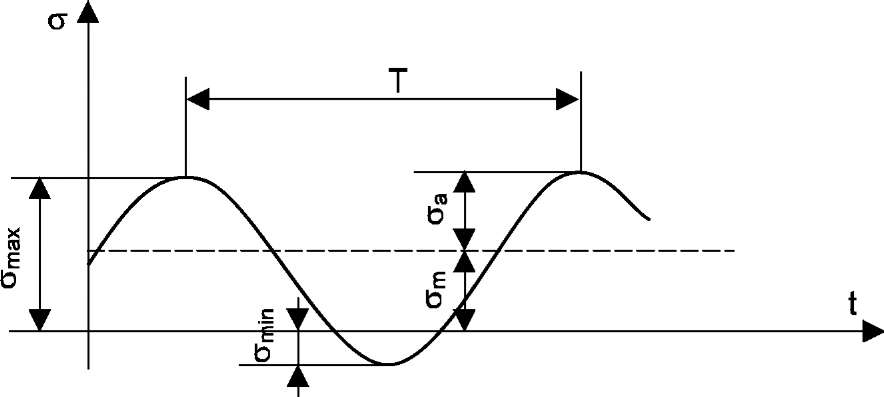
Рис 1. Изменение напряжений во времени

а - симметричный цикл, б - знакопостоянный,

в - пульсационный цикл, г – знакопеременный

Рассмотрим основные характеристики цикла. Отношение наименьшего напряжения цикла к наибольшему называется коэффициентом асимметрии цикла:

Для симметричного цикла (рис. 1а) , а коэффициент асимметрии r = -1. Любой цикл напряжений характеризуется двумя параметрами:

,

где - среднее постоянное напряжение цикла, - амплитуда цикла.

Разность называется размахом напряжений.

Процесс образования трещины при переменных напряжениях связан с накоплением пластических деформаций. Поэтому следует ожидать, что усталостное разрушение определяется только напряжениями и . Кроме того, как показывают опыты, несущественным является влияние частоты изменения напряжений. Исключения представляют испытания при высоких температурах, а также при воздействии коррозионной среды. В итоге для оценки усталостного разрушения в условиях заданного цикла достаточно знать только величины и или и .

Наиболее распространенными являются испытания в условиях симметричного цикла. В этом случае полученное значение предела выносливости обозначается .

Первую машину для усталостных испытаний в средине 19 века построил А. Велер.

Для получения характеристик сопротивления усталости необходимо провести испытания не менее десяти одинаковых образцов. При этом каждый образец испытывают только при одной амплитуде напряжений до разрушения (или до базового числа циклов). Процесс испытаний достаточно длительный.

Около половины партии образцов испытывается при напряжении, имеющих уровень 0,7 - 0,5 от предела прочности .

Испытания проводят в следующей последовательности. Для первого образца устанавливают напряжения 0,7 , нагружают его до разрушения и фиксируют число циклов N. которое выдержал образец. Для последующих образцов процесс повторяется при постепенном снижении максимального уровня напряжений .

По данным испытаний ( и N) для каждого образца строят кривую усталости (кривую Велера). Кривая строится в полулогарифмической системе координат: по оси ординат откладываются , а оси абсцисс - logN. На рис. 2 приведена кривая усталости для малоуглеродистой стали.

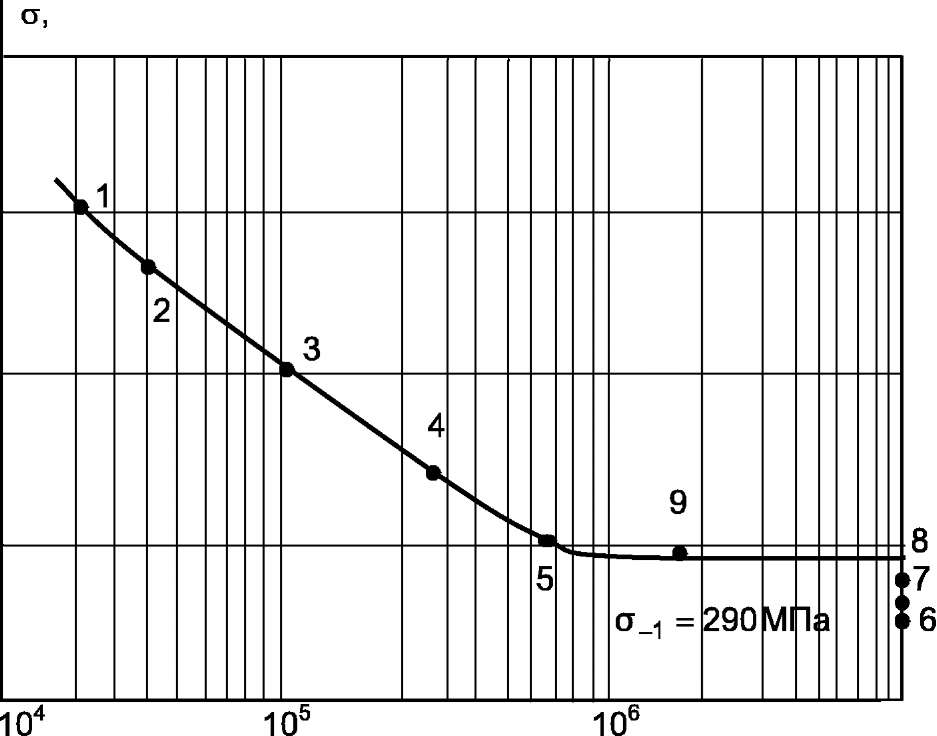
Рис. 2. Кривая усталости

Кривая Велера асимптотически приближается к наибольшему значению напряжения цикла, при котором образец не разрушается до базы испытаний. Это напряжение является пределом выносливости .