9.5. Эмпирические формулы для определения критических напряжений
Если, как это очень часто случается на практике, гибкость стержней будет меньше указанных значений, то формула Эйлера становится неприменимой, так как критические напряжения превзойдут предел пропорциональности и закон Гука потеряет силу.
Существуют приближенные теоретические методы определения критических сил при потере устойчивости в неупругой стадии, но их рассмотрение выходит, за рамки настоящего курса.
В этих случаях обычно пользуются следующей эмпирической формулой Тетмайера Ясинского, полученной на основании многочисленных опытов:
(9.11)
где а и b коэффициенты, зависящие от материала.
Для стали Ст.З при гибкостях λ = 40÷100 коэффициенты а и b могут быть приняты равными: а = 310 МПа, b = 1,14 МПа.
При гибкостях λ<40 стержни можно рассчитывать на прочность без учета опасности продольного изгиба.
9.6. Практическая формула для расчета на устойчивость
Вместо двух формул (Эйлера и Ясинского), каждая из которых пригодна для определенного диапазона гибкостей, удобнее иметь одну формулу, которой можно было бы пользоваться при любой гибкости стержня.
Эта практическая формула, широко применяющаяся при расчете строительных конструкций, имеет вид
(9.12)
где
основное допускаемое напряжение на
сжатие;
коэффициент
уменьшения основного допускаемого
напряжения (или
коэффициент продольного изгиба).
Величина
зависит от материала и гибкости стержня.
Его значения приведены в табл. 9.1; А
площадь поперечного сечения стержня.
Величина
может рассматриваться как допускаемое
напряжение при расчете на устойчивость,
т.е.
(9.13)
Основное допускаемое напряжение на сжатие имеет вид:
(9.14)
где предельное напряжение, принимаемое равным пределу текучести для пластичных материалов или пределу прочности для хрупких материалов.
Связь между
коэффициентом
,
критическим напряжением
предельным
напряжением
и коэффициентами запаса прочности n
и устойчивости
,
можно установить следующим образом:
откуда
(9.15)
Используя формулу (9.14), получим
(9.16)
Для подбора сечения формулу приводят к следующему виду:
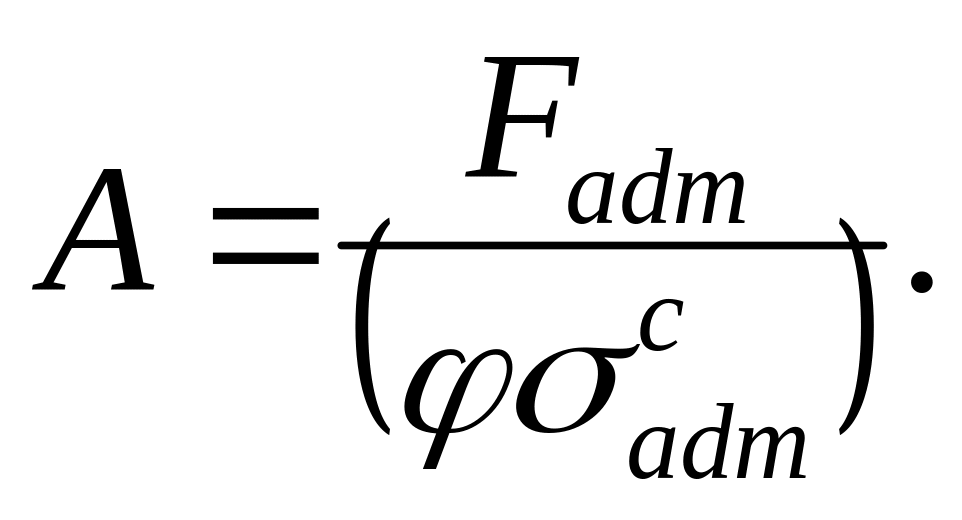(9.17)
При этом значением
(
приходится задаваться, так как гибкость
λ
неизвестна,
ибо неизвестна площадь, сечения A,
а гибкость зависит от нее. В качестве,
imin,
λ по табл.
9.1 находят соответствующее значение
(
)
первого приближения рекомендуется
принимать
=0,5.
Затем определяют величины А, min.
Если получается
большая разница между значениями
и
то следует
повторить расчет, задавшись новым
значением (
):
и т.д., пока разница между последовательными значениями не будет превышать 4-6 %.
Для стержней, сечения которых имеют значительные ослабления (например, от отверстий), кроме расчета на устойчивость должен производиться и обычный расчет на прочность по формуле
(9.18)
где Аnt рабочая (нетто) площадь сечения стержня.
При расчете же на устойчивость берется полная площадь сечения Аbr.
В некоторых случаях (например, при расчете элементов машиностроительных конструкций) значения коэффициентов запаса устойчивости ns, предусмотренные при составлении таблиц коэффициентов (ns=1,8), недостаточны.
В этих случаях расчет следует вести, исходя непосредственно из требуемого коэффициента ns и пользуясь формулой Эйлера или Ясинского. Так же следует поступать при расчете на устойчивость стержней из материалов, которые не отражены в таблице коэффициентов .
Таблица 9.1.
Гибкость
|
для |
||||
сталей Ст.1, Ст.2, Ст.3, Ст.4 |
стали Ст.5 |
Стали повышенного
качества |
чугуна |
дерева |
|
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 |
1,00 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75 0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19 |
1,00 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70 0,62 0,51 0,43 0,37 0,33 0,29 0,26 0,24 0,21 0,19 0,17 0,16 |
1,00 0,97 0,95 0,91 0,87 0,83 0,79 0,72 0,65 0,55 0,43 0,35 0,30 0,26 0,23 0,21 0,19 0,17 0,15 0,14 0,13 |
1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,20 0,16 - - - - - - - - - - |
1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08 |
