9.3. Влияние способа закрепления концов стержня на критическую силу

Чаще всего концы стержня закрепляют одним из четырех способов, показанных на рис. 9.4.

Второй способ  шарнирное закрепление обоих концов  рассмотрен нами при выводе формулы Эйлера.

При других способах закрепления обобщенная формула Эйлера для определения критической нагрузки имеет вид

(9.7)

где (μ  коэффициент приведения длины стержня), зависящий от способа закрепления концов стержня;  приведенная длина стержня.

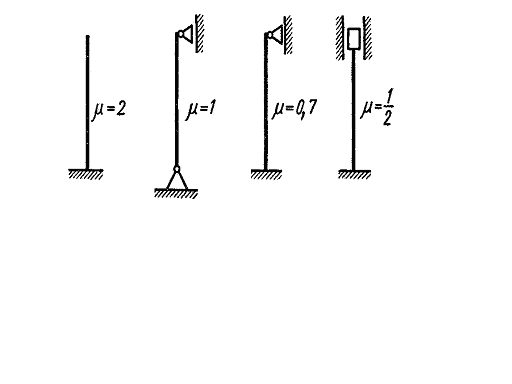
Рис. 9.4.

Формула (9.7) получается, если рассмотреть дифференциальное уравнение продольного изгиба

которое следует из уравнения после двукратного дифференцирования.

Решение этого уравнения имеет вид

Постоянные К, В, С, D определяются из граничных условий. Например, для третьего случая закрепления (рис. 9.4) при начале координат на нижнем конце имеем (  длина стержня):

Используя эти условия, получим

Из математики известно, что система однородных уравнений (т.е. без свободных членов) имеет ненулевое решение только в том случае, когда ее определитель равен нулю:

Раскрывая этот определитель, получим . Наименьший корень этого уравнения, отличный от нуля, , тогда

Таким образом, = 0,7.

Аналогично получают значения коэффициентов, указанные на рис. 9.4, при других способах закрепления концов стержня.

Как видно из формулы (9.7), чем меньше , тем больше критическая, а следовательно, и допускаемая нагрузка стержня. Например, нагрузка стержня, заделанного двумя концами, может быть в 16 раз больше нагрузки стержня, заделанного одним концом. Поэтому там, где возможно, следует осуществлять жесткую заделку обоих концов стержня. Однако это не всегда можно осуществить на практике. Элементы, к которым прикрепляются концы рассматриваемого стержня, всегда более или менее упруги, податливы, что вносит некоторую неопределенность в расчет. Поэтому весьма часто даже при жестком соединении концов стержня с другими элементами расчет в запас устойчивости ведут, предполагая шарнирное закрепление обоих концов.

9.4. Пределы применимости формулы Эйлера

Формулой Эйлера не всегда можно пользоваться. При ее выводе мы пользовались дифференциальным уравнением упругой линии, вывод которого основан на законе Гука. Закон же Гука, как известно, справедлив до тех пор, пока напряжения не превосходят предела пропорциональности. Чтобы установить пределы применимости формулы Эйлера, определим критическое напряжение , т. е. напряжение, возникающее в поперечном сечении стержня при действии критической нагрузки:

(9.8)

где А  площадь поперечного сечения стержня.

Но  наименьший радиус инерции поперечного сечения стержня. Поэтому формулу (9.8) можно записать в виде

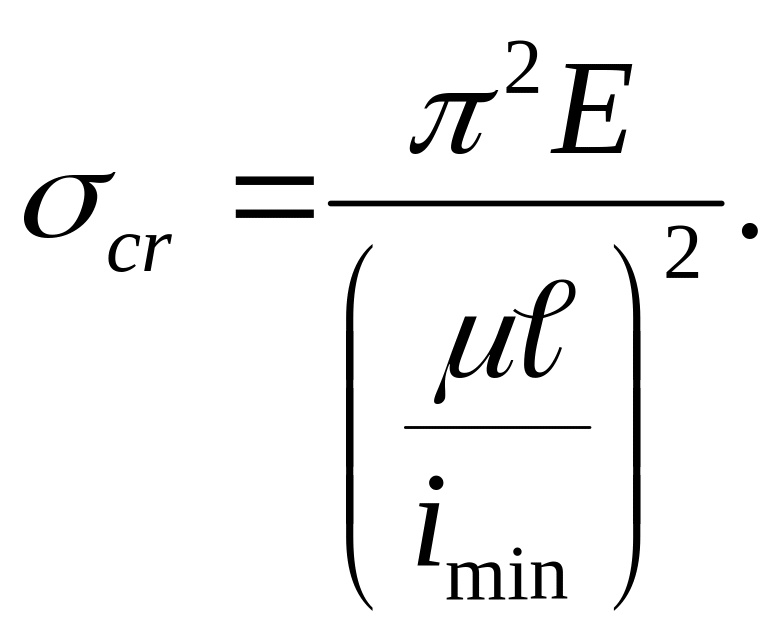
Величина характеризует влияние размеров стержня и способа закрепления концов; она называется гибкостью стержня и обозначается λ. Гибкость  величина безразмерная.

Таким образом, обозначая получаем

Чтобы можно было пользоваться формулой Эйлера, необходимо удовлетворить следующему условию:

(9.9)

где  предел пропорциональности материала стержня.

Записывая формулу (9.9) относительно гибкости, получаем условие применимости формулы Эйлера в виде

(9.10)

Например, для стали Ст.З =200 МПа и

Таким образом, для стержней из малоуглеродистой стали формула Эйлера применима, если их гибкость больше 100.

Аналогичным образом получим условия применимости формулы Эйлера для чугуна λ  80. Для средне и высокоуглеродистых, а также для легированных сталей формула Эйлера применима и при гибкости, меньшей указанной. Так для стержней из хромомолибденовой стали формула Эйлера применима при λ 70.