7.4. Кручение с изгибом

Брус, изображенный на рис. 7.5, работает на кручение и изгиб. В машиностроительных конструкциях детали, работающие на кручение и изгиб, встречаются очень часто. Характерным примером таких деталей являются валы различных машин.

Начнем с того, что, пользуясь принципом независимости действия сил, определим отдельно напряжения, возникающие в брусе при кручении, и отдельно  при изгибе. При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах балки: и касательные напряжения, достигающие наибольшего значения у нейтральной оси. От кручения в поперечных сечениях возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения;

В случае, изображенном на рис. 7.5, сечение, где возникает наибольший изгибающий момент, совпадает с сечением, где возникает наибольший крутящий момент. Это сечение у заделки. В этом сечении (опасном) опасными являются точки С и В. Рассмотрим напряженное состояние в точке С. Но площадке поперечного сечения, проходящего через эту точку, действуют наибольшие касательные напряжения от кручения и наибольшие (в данном случае растягивающие) нормальные напряжения от изгиба

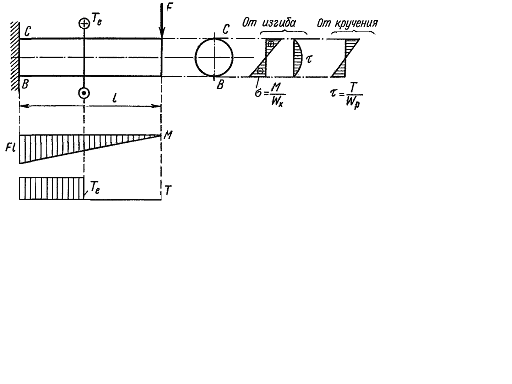
Рис. 7.5.

По площадке продольного сечения нормальные напряжения отсутствуют, а касательные (в силу закона парности) имеют то же значение, что и в поперечном сечении.

Так как напряженное состояние двухосное, то для проверки прочности применяем одну из гипотез прочности. Имея в виду валы, изготовленные из стали, применяем третью или четвертую гипотезу прочности. Для этого необходимо определить главные напряжения для заданного напряжения состояния (рис. 7.6).

Главные напряжения определяются по известной формуле

(7.28)

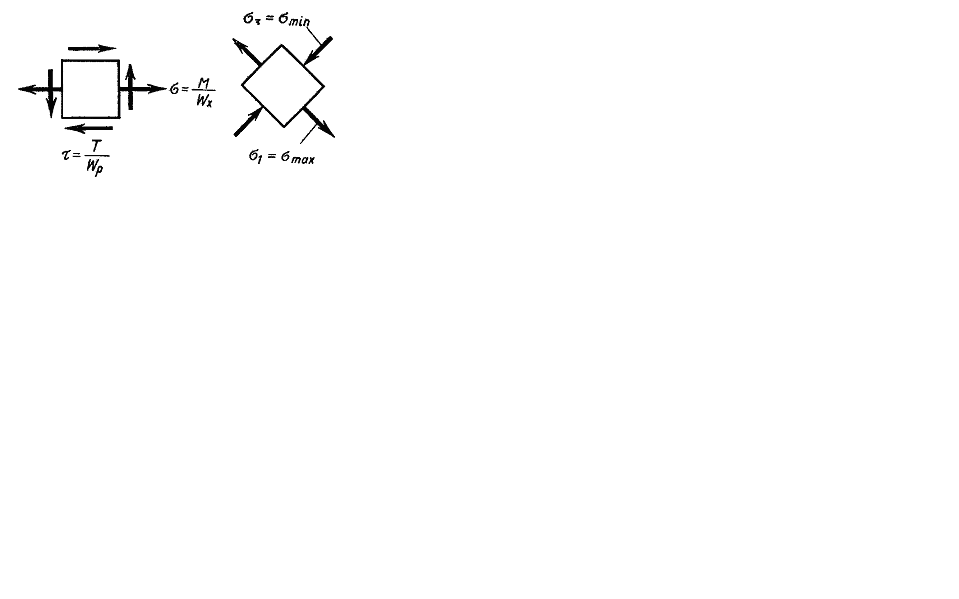
Рис. 7.6.

Условие прочности  по третьей гипотезе (гипотеза наибольших касательных напряжений),

Подставляя сюда значения и , получаем

(7.29)

Учитывая, что и , получаем

(7.30)

Отсюда получим зависимость для подбора сечения (проектного расчета):

(7.31)

Напоминаем, что в случае, если вал испытывает изгиб в двух взаимно перпендикулярных плоскостях, то

(7.32)

По четвертой гипотезе прочности (гипотезе удельной потенциальной энергии изменения формы), условие прочности для случая плоского напряженного состояния имеет вид

(7.33)

Подставляя значения и , выраженные через и в поперечном сечении вала, получаем

_(7.34)

но и , следовательно,

_(7.35)

Отсюда для подбора сечения

(7.36)

7.5. Кручение с растяжением (сжатием)

В этом случае в поперечных сечениях стержня возникают одновременно два внутренних усилия: крутящий момент и продольная сила (растягивающая или сжимающая).

Для стержня круглого сечения наибольшие касательные напряжения при кручении имеют место в точках контура сечения При растяжении во всех точках поперечного сечения возникают нормальные напряжения

Теперь, так же как и в случае кручения с изгибом, следует определить главные напряжения и применить соответствующую гипотезу прочности. В результате получим для эквивалентных напряжений формулу (7.29) (по третьей гипотезе прочности) или (7.34) (по четвертой гипотезе). В эти формулы следует подставить значения и , приведенные выше.

Окончательно получим условие прочности для кручения с растяжением (сжатием):

а) по третьей гипотезе прочности,

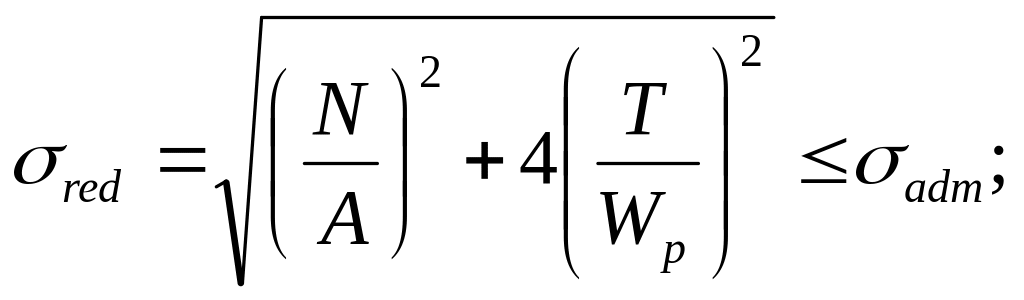(7.37)

б) по четвертой гипотезе прочности,

(7.38)

Рекомендуется отдавать предпочтение формуле (7.38), так как четвертая гипотеза для пластичных материалов хорошо согласуется с опытными данными и приводит к более экономичным решениям.