
- •1. Основные понятия и положения 11
- •2. Центральное растяжение и сжатие стержня 17
- •3. Геометрические характеристики плоских сечений 42
- •4. Кручение 49
- •5. Изгиб стержней 57
- •Introduction 173
- •1. Basic concepts and principles 175
- •2. Tension and compression of a bar 181
- •3. Geometric characteristics of cross sections 202
- •4. Torsion 208
- •5. Bending of bars 216
- •Index 405 введение
- •1. Основные понятия и положения
- •1.1. Задачи сопротивления материалов, основные гипотезы и допущения
- •1.2. Типы нагрузок и деформаций
- •1.3. Определение внутренних усилий методом сечений. Напряжения
- •2. Центральное растяжение и сжатие стержня
- •2.1. Напряжения и продольная деформация при растяжении и сжатии
- •2.2. Закон Гука при растяжении и сжатии
- •2.3. Поперечная деформация при растяжении и сжатии
- •2.4. Диаграмма растяжения низкоуглеродистой стали
- •2.5. Потенциальная энергия деформации при растяжении
- •2.6. Расчеты на прочность при растяжении и сжатии
- •2.7. Статически неопределимые задачи
- •2.8. Напряжения в наклонных сечениях при растяжении (сжатии) в одном направлении
- •2.9. Закон парности касательных напряжений
- •2.10. Определение напряжений в наклонных сечениях при растяжении (сжатии) в двух направлениях
- •2.11. Определение главных напряжений и положения главных площадок
- •2.12. Зависимость между деформациями и напряжениями при плоском и объемном напряженных состояниях (обобщенный закон Гука)
- •2.13. Работа внешних и внутренних сил при растяжении (сжатии). Потенциальная энергия деформации
- •3. Геометрические характеристики плоских сечений
- •3.1. Статический момент площади
- •3.2. Полярный момент инерции
- •3.3. Осевой момент инерции
- •3.4. Момент инерции при параллельном переносе осей
- •3.5. Главные оси и главные моменты инерции
- •4. Кручение
- •4.1. Определение крутящего момента
- •4.2. Определение напряжений в стержнях круглого сечения
- •4.3. Деформации и перемещения при кручении валов
- •4.4. Потенциальная энергия при кручении
- •5. Изгиб стержней
- •5.1. Типы опор балок
- •5.2. Определение опорных реакций
- •5.3. Определение внутренних усилий при изгибе
- •5.4. Правило знаков для изгибающих моментов и поперечных сил
- •5.5. Дифференциальные зависимости при изгибе
- •5.6. Построение эпюр изгибающих моментов и поперечных сил
- •5.7. Определение нормальных напряжений
- •5.8. Условия прочности по нормальным напряжениям
- •5.9. Потенциальная энергия деформации при изгибе
- •5.10. Теорема о взаимности работ. Теорема о взаимности перемещений
- •5.11. Определение перемещений методом Мора
- •6. Теории прочности
- •6.1. Назначение гипотез прочности
- •6.2. Первая гипотеза прочности
- •6.3. Вторая и третья гипотезы прочности
- •6.4. Энергетические гипотезы прочности
- •7. Сложное сопротивление
- •7.1. Изгиб в двух плоскостях (косой изгиб)
- •7.2. Изгиб с растяжением (сжатием)
- •7.3. Внецентренное сжатие (растяжение)
- •7.4. Кручение с изгибом
- •7.5. Кручение с растяжением (сжатием)
- •7.6. Пример расчета вала на изгиб с кручением
- •8. Расчет тонкостенных сосудов
- •9. Расчет сжатых стержней на устойчивость (продольный изгиб)
- •9.1. Устойчивые и неустойчивые формы равновесия
- •9.2. Формула Эйлера для критической силы
- •9.3. Влияние способа закрепления концов стержня на критическую силу
- •9.4. Пределы применимости формулы Эйлера
- •9.5. Эмпирические формулы для определения критических напряжений
- •9.6. Практическая формула для расчета на устойчивость
- •10. Динамическое действие нагрузок
- •10.1. Динамические нагрузки
- •10.2. Вычисление напряжений при равноускоренном движении
- •10.3. Определение перемещений и напряжений при ударе
- •11. Расчет на прочность при напряжениях, циклически изменяющихся во времени (расчет на усталость)
- •11.1. Основные определения
- •11.2. Кривая усталости при симметричном цикле. Предел выносливости
- •11.3. Диаграммы предельных напряжений и амплитуд цикла
- •11.4. Факторы, влияющие на предел выносливости
- •11.5. Определение коэффициента запаса прочности при симметричном цикле
- •11.6. Определение коэффициента запаса прочности при асимметричном цикле напряжений
- •Предположим, что при увеличении нагрузки на деталь отношение Такое нагружение называется простым.
- •11.7. Практические меры повышения сопротивления усталости
- •Практикум Лабораторная работа № 1
- •Введение
- •Установка
- •Порядок выполнения
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 2
- •Введение
- •Установка
- •Порядок выполнения
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 3
- •Введение
- •Установка
- •Порядок выполнения
- •Introduction
- •Basic concepts and principles
- •Tasks, main hypothesis and assumptions of the strength of materials
- •1.2. Types of loads and deformations
- •1.3. Determining the internal forces by the method of sections. Stresses
- •2. Tension and compression of a bar
- •2.1. Stresses and a longitudinal deformation in tension and compression
- •2.2. Hooke,s law in tension and compression
- •2.3. The transverse deformation in tension and compression
- •2.4. The tension diagram of the lowcarbon steel
- •2.5. The potential deformation energy in tension
- •2.6. Strength calculation in tension and compression
- •2.7. Statically indeterminate problems
- •2.8. Stresses at inclined sections under tension (compression) in one direction
- •2.9. Law of the shearing stresses couple
- •2.10. Determination of stresses at the inclined sections in tension (compression) in two directions
- •2.11. Determining the principal stresses and the principal planes position
- •2.12. The relation between the deformations and the stresses for the plane and general stresses (a general form of Hook’s law)
- •2.13. The work of the external and internal forces in tension (compression). Strain energy
- •3. Geometric characteristics of cross sections
- •3.1. First moment of an area
- •3.2. Polar moment of inertia
- •3.3. Axial moment of inertia
- •3.4. The moment of inertia at parallel displacement of axis
- •3.5. Principal axes and principal moment of inertia
- •4. Torsion
- •4.1. Determining the twisting moment
- •4.2. Determining the stresses in the round section bar
- •4.3. The deformations and displacements in the shaft torsion
- •4.4. Internal strain energy in torsion
- •5. Bending of bars
- •5.1. Types of the beam support
- •5.2. Determining the support reactions
- •5.3. Determining the internal stresses in bending
- •5.4. The sign rule for the bending moments and the shearing forces
- •5.5. The differential relationships in bending
- •I.E. The intensity of the distributed load is equal to the derivative of the shearing force with respect to the bar section abscissa.
- •I.E. The shearing force is equal to the derivative of the bending moment with respect to the bar section abscissa.
- •I.E. The second derivative of the bending moment with respect to the bar section abscissa is equal to the intensity of the distributed load.
- •5.6. Drawing bending moment and shearing force diagrams
- •5.7. Determining the normal stress
- •5.8. Strength conditions with normal stresses
- •5.9. Strain energy in bending
- •5.10. Betty’s reciprocal theorem. Reciprocal displacement theorem
- •5.11. Determining displacements by Mohr’s method
- •6. Strengtn theory
- •6.1. The purpose of strength hypotheses
- •6.2. The first strength hypothesis
- •6.3. The second and third strength hypotheses
- •6.4. The energy hypotheses of strength
- •7. Combined stress
- •7.1. Bending in two planes (non-uniplanar bending)
- •7.2. Combined axial tension (compression) and bending
- •7.3. Eceentrical tension (compression)
- •7.4. Combined torsion and bending
- •7.5. Combined torsion and compression
- •7.6. Example of the shaft calculation in bending with torsion
- •8. Calculation of the thin-walled vessels
- •9. Stability analysis of the bars in compression (buckling)
- •9.1. Stable and unstable equilibrium forms
- •9.2. Euler’s formula for the critical force
- •9.3. Influence of bar end conditions on the critical force
- •9.4. Applicability limits of of Euler’s formula
- •9.5. Empirical formula for determining the critical stresses
- •9.6. The practical formula for the stability analysis
- •10. Dynamic load action
- •10.1. Dynamic load
- •10.2. Calculating stresses under the uniformly accelerated motion
- •10.3. Determining displacements and stresses under the impact
- •11. Stress analysis under the stresses changing cyclically in time
- •11.1. Basic definitions
- •11.2. Fatigue (Wohler’s) curve under the symmetrical cycle. Fatigue strength
- •11.3. The limit stress diagram and the cycle amplitude
- •11.4. Factors influencing on the fatigue strength
- •11.5. Determining the factor of safety under the symmetrical cycle
- •11.6. Determining the factor of safety under the asymmetrical stress cycle
- •11.7. Practical measures to increase the fatigue strength
- •Practicum Laboratory work № 1
- •Introduction
- •Installation
- •Test specimens
- •Test questions
- •Literature
- •Laboratory work № 2
- •Introduction
- •Installation
- •Test questions
- •Literature
- •Laboratory work № 3
- •Introduction
- •Installation
- •Individual task report
- •Test questions
- •Literature
- •Англо-русский терминологический словарь
- •Список фамилий ученых
- •Greek alphabet
- •Сокращения
- •Единицы измерения
- •Список наиболее употребительных знаков
- •Список использованной литературы
- •Алфавитный указатель
- •Сопротивление материалов
- •625000, Тюмень, ул. Володарского, 38.
- •625039, Г. Тюмень, ул. Киевская, 52
5.8. Условия прочности по нормальным напряжениям
Для обеспечения прочности балки необходимо, чтобы наибольшие растягивающие и наибольшие сжимающие напряжения при изгибе в опасном сечении, т. е. в сечении, где М имеет наибольшее значение, не превосходили соответствующих допускаемых напряжений (рассматриваются только балки с постоянным по всей длине поперечным сечением).
Обозначим (рис. 5.10 б) ht расстояние до наиболее удаленного от нейтральной оси растянутого волокна, hc расстояние до наиболее сжатого волокна. Тогда наибольшее растягивающее напряжение при изгибе наибольшее сжимающее напряжение (взятое по абсолютному значению)
![]() (5.15)
(5.15)
![]() (5.16)
(5.16)
Для хрупких материалов (например, чугуна) допускаемые напряжения на растяжение и сжатие различны. Поэтому для балок из таких материалов обычно применяют сечения, не симметричные относительно нейтральной оси. При этом сечение располагают таким образом, чтобы ht < hc. В указанных случаях надо составлять два условия прочности:
по наибольшим растягивающим напряжениям
![]() (5.17)
(5.17)
по наибольшим сжимающим напряжениям
![]() (5.18)
(5.18)
где Wxt и Wxc моменты сопротивления растянутого и сжатого волокон.
Если сечение балки симметрично относительно нейтральной оси (такие сечения целесообразно применять для балок из пластичных материалов), то получим формулу
![]() (5.19)
(5.19)
Обозначив,
![]() получим при одинаковых допускаемых
напряжениях на растяжение и сжатие
получим при одинаковых допускаемых
напряжениях на растяжение и сжатие
![]() следующее
условие прочности:
следующее
условие прочности:
![]() (5.20)
(5.20)
Величина Wx называется осевым моментом сопротивления или моментом сопротивления при изгибе.
Пример. Подобрать
сечение балки двутаврового профиля
пролетом
L=6
м, нагруженной равномерно распределенной
нагрузкой q
= 40
кН/м,
![]() =
160 МПа =
160.103
кПа.
=
160 МПа =
160.103
кПа.
Решение. Для этого случая наибольший изгибающий момент имеет место в среднем cечении балки:
![]()
Требуемый момент сопротивления
![]()
Из таблиц сортамента выбираем двутавр № 45, у которого Wx = 1231 см3 (при этом Wx будет недонапряжение < 5%, что допустимо).
5.9. Потенциальная энергия деформации при изгибе
При изгибе работа, производимая внешними силами, затрачивается на изменение потенциальной энергии деформированного стержня. Работа внешнего момента Ме может быть вычислена по формуле
![]() ,
,
где угол поворота сечения в точке приложения момента.
Элементарная работа изгибающего момента может быть найдена по формуле:
![]() (5.21)
(5.21)
Полная работа изгибающих моментов для балки длиной L
![]() (5.22)
(5.22)
Потенциальную энергию изгиба, равную работе внутренних сил, взятую с обратным знаком, можно определить по формуле
![]() (5.23)
(5.23)
В общем случае изгиба в поперечных сечениях балки кроме изгибающих моментов возникают еще и поперечные силы.
Однако потенциальная энергия сдвига, соответствующая работе поперечной силы, как показывают исследования, невелика, и ею, обычно пренебрегают.
Поэтому формула (5.23) пригодна и для чистого, и для общего случая изгиба.
5.10. Теорема о взаимности работ. Теорема о взаимности перемещений
Докажем теорему, имеющую важные приложения, а именно теорему о взаимности работ. Для этого рассмотрим какую-нибудь линейно-деформируемую систему в двух различных, состояниях, отвечающих двум различным нагрузкам (рис. 5.11) Для простоты выкладок рассмотрим простую балку, нагруженную в обоих состояниях самой простой нагрузкой (по одной сосредоточенной силе). Нагрузка, внутренние усилия и деформации, соответствующие этим состояниям, отмечены индексами 1 и 2.
На рис. 5.11 а изображено первое состояние системы, а на рис. 5.11 б второе.
Перемещение по направлению нагрузки в первом состоянии от этой же нагрузки обозначено ∆11. Перемещение по направлению нагрузки второго состояния, вызванное действием нагрузки первого состояния, обозначено ∆21. Обозначения перемещений второго состояния приведены на рис. 5.11 б. Перемещения, содержащие в своем обозначении два одинаковых индекса, как, например, ∆11 ,∆22, называются главными, а перемещения вида ∆ 21, ∆ 12 и т. д. побочными. Докажем теперь теорему о взаимности работ, а именно: работа внешних сил первого состояния на перемещениях второго состояния равна работе сил второго состояния на перемещениях, вызванных силами первого состояния.
а)
б)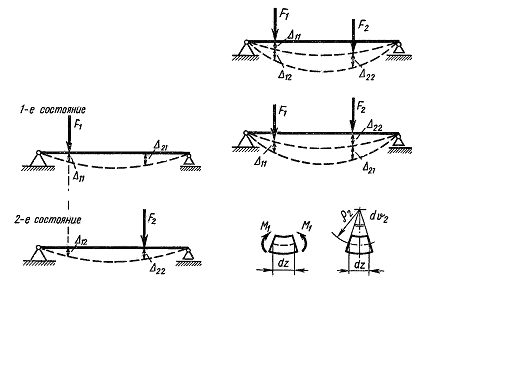
а)
б)
Рис. 5.11. Рис. 5.12.
Для доказательства теоремы нагрузим балку силами F1 и F2 , прикладывая их в разной последовательности.
1. Вначале приложим нагрузку F1, а затем к деформированной балке приложим силу F2 (рис. 5.12 а).
Подсчитаем работу, произведенную при этом внешними силами.
Работа, произведенная
силой
F1
на собственном
перемещении ∆11
вызванном
этой силой,
![]() Работа, произведенная силой F2
на собственном перемещении ∆22,
Работа, произведенная силой F2
на собственном перемещении ∆22,
![]()
Дополнительная
работа силы F1
на перемещении
∆12,
вызванном силой F2,
![]()
Обращаем внимание на то, что при вычислении W12 множитель 1/2 отсутствует, так как сила F на перемещении ∆12 совершает работу, оставаясь постоянной.
Полная работа, совершенная внешними силами при первом способе (последовательности) нагружения,
![]() (5.24)
(5.24)
Работа W12, фактически совершаемая силой на перемещениях, вызванных другой силой (силами), называется дополнительной работой. Однако эта работа может и не совершаться, а может рассматриваться лишь как возможная, т. е. такая, которая будет произведена, если нагрузить систему сразу обеими нагрузками. Такую работу называют виртуальной (возможной) работой.
При дальнейших выкладках не будем делать различия между дополнительной и виртуальной работой.
2. Нагрузим теперь балку в другой последовательности: вначале приложим силу F2, а затем силу F1 (рис. 5.12 б). Работа, произведенная силой F2 на собственном перемещении ∆22,
![]() (5.25)
(5.25)
Работа, произведенная силой F1 на собственном перемещении ∆11,
![]() (5.26)
(5.26)
Работа, произведенная силой F2 на перемещении ∆21 ,
![]() (5.27)
(5.27)
Полная работа при втором способе нагружения
![]() (5.28)
(5.28)
Однако работа сил не зависит от порядка их приложения. Следовательно, W1 = W11, откуда получим
![]() (5.29)
(5.29)
или для рассматриваемого случая
![]() (5.30)
(5.30)
Этим доказана сформулированная выше теорема о взаимности виртуальных работ внешних сил. Мы доказали ее на примере сосредоточенных внешних нагрузок. Однако теорема остается справедливой и для любой внешней нагрузки: сосредоточенной, распределенной, внешних моментов. Следует только иметь в виду, что работа моментов вычисляется уже не на линейных, а на угловых перемещениях.
Аналогичным образом может быть доказана также взаимность виртуальной работы внутренних сил:
![]() (5.31)
(5.31)
Используя закон
сохранения энергии, можно показать, что
дополнительная работа внешних сил равна
по абсолютному значению дополнительной
работе внутренних сил:
![]() и
и
![]()
Из этого следует также, что
![]() (5.32)
(5.32)
Эти соотношения будут использованы далее для обоснования общего метода определения перемещений (метода Мора). Из теоремы о взаимности работ как частный случай следует другая важная теорема о взаимности перемещений.
Принимая F1 = F2 =1, получим
![]() (5.33)
(5.33)
Здесь перемещения,
вызываемые силами, равными единице
(единичными силами), обозначают
![]() и т. д.
и т. д.
Перемещение точки приложения единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по направлению последней, вызванному действием первой единичной силы.
