4.3. Деформации и перемещения при кручении валов

Для вычисления деформаций вала при кручении воспользуемся формулой (4.7):

Деформация вала на длине z (взаимный угол поворота сечений) равна

Если крутящий момент и величина GI_p, называемая жесткостью вала при кручении, постоянны на всем участке интегрирования, то

Аналогично, для вала длиной получим

(4.15)

4.4. Потенциальная энергия при кручении

При кручении внешние моменты совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил.

Работа статически приложенного внешнего скручивающего момента равна половине произведения конечного значения момента на окончательный угол закручивания:

(4.16)

Работа внутренних сил, отрицательная по знаку, и численно равная ей потенциальная энергия

(4.17)

где Т  крутящий момент; d  угол закручивания элемента длиной dz.

Но по формуле (4.17),

.

Следовательно,

(4.18)

Полную работу внутренних сил получим, интегрируя выражение для элементарной работы по всей длине стержня:

Для вычисления потенциальной энергии, равной по значению работе внутренних сил и обратной по знаку, имеем

(4.19)

5. Изгиб стержней

Часто стержни подвергаются действию поперечной нагрузки или внешних пар (рис. 5.1). При этом в поперечных сечениях стержня возникают изгибающие моменты, т. е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

При действии такой нагрузки ось, стержня искривляется. Указанный вид нагружения называют изгибом, а стержни, работающие в основном на изгиб  балками.

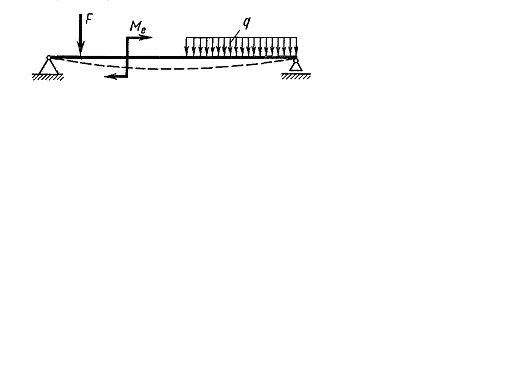
Рис. 5.1.

Изгиб называют чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

В поперечных сечениях стержня наряду с изгибающими моментами возникают также и поперечные силы. Такой изгиб называют поперечным. Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных центральных осей поперечного сечения стержня, изгиб носит название простого или плоского.

Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, изгиб называют косым. При косом изгибе плоскость деформации не совпадает с силовой плоскостью.

5.1. Типы опор балок

Опоры балок, рассматриваемых как плоские системы, бывают трех основных типов.

1. Подвижная шарнирная опора (рис. 5.2 а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка. Схематическое изображение подвижной шарнирной опоры дано на рис. 5.2 б.

а) б) в) г)

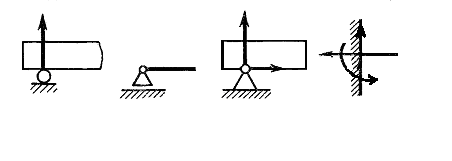
Рис. 5.2.

Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.

2. Неподвижная шарнирная опора (рис. 5.2 в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие  горизонтальную и вертикальную.

3. Жесткая заделка, или защемление (рис. 5.2 г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).

Балка с одним заделанным концом называется консольной балкой или просто консолью.

Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реакций в таких балках приходится составлять дополнительные уравнения  уравнения перемещений.