2.13. Работа внешних и внутренних сил при растяжении (сжатии). Потенциальная энергия деформации

При растяжении (сжатии) внешние силы совершают работу вследствие перемещения точек их приложения (рис. 2.10 а).

Вычислим работу статически приложенной внешней силы, т. е. такой силы, которая растет в процессе деформации от нуля до своего конечного значения с весьма небольшой скоростью.

Рис. 2.10.

Элементарная работа dW внешней силы F на перемещении равна

. (2.22)

Но между и F существует зависимость (закон Гука)

Подставляя это значение в формулу (2.22), получаем

Полную работу силы получим, интегрируя это выражение в пределах от нуля до окончательного значения перемещения :

Таким образом,

(2.23)

т. е. работа внешней статически приложенной силы равна половине произведения окончательного значения силы на окончательную величину соответствующего перемещения.

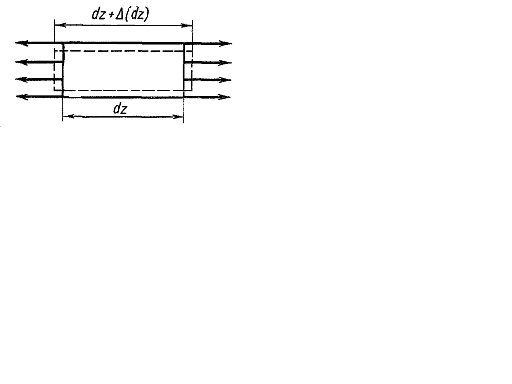
Рис. 2.11.

Графически работа силы F выражается (с учетом масштабов) площадью ОСВ диаграммы, построенной в координатах (рис. 2.11, б).

Отметим, что работа силы неизменной по значению, на перемещении равна

(2.24)

При деформации совершают работу не только внешние силы, но и внутренние (силы упругости).

Элементарная работа внутренних сил (для элемента dz) вычисляется по формуле (рис. 2.11):

(2.25)

где N – внутреннее усилие (продольная сила); ∆(dz) – удлинение элемента.

Но, согласно закону Гука имеем Следовательно,

(2.26)

Полную работу внутренних сил получим, интегрируя обе части формулы (26) по длине всего стержня

. (2.27)

Если N, E и A постоянны, то

, (2.28)

где – удлинение стержня.

Величина, равная работе внутренних сил, но имеющая противоположный знак, называется потенциальной энергией деформации.

Она представляет собой энергию, накапливаемую телом при деформации.

Таким образом, для стержня постоянного сечения при продольной силе, имеющей одно и то же значение во всех поперечных сечениях, потенциальная энергия при растяжении (сжатии) определяется по формуле

. (2.29)

Потенциальная энергия, отнесенная к единице объема материала, называется удельной потенциальной энергией:

(2.30)

или

так как или (2.31)

При объемном напряженном состоянии удельная потенциальная энергия получится как сумма трех слагаемых:

(2.32)

Используя обобщенный закон Гука, получаем

(2.33)

Из этой формулы как частный случай, полагая одно из главных напряжений равным нулю, легко получить формулу для плоского напряженного состояния.

3. Геометрические характеристики плоских сечений

3.1. Статический момент площади

При некоторых деформациях прочность деталей зависит не только от площади поперечного сечения, но и от его формы. До сих пор мы изучали деформации, у которых напряжения зависели только от площади поперечного сечения. В дальнейшем для изучения деформаций кручения и изгиба нам потребуется знание некоторых других геометрических характеристик плоских фигур.

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на расстояния от них до этой оси (рис. 3.1).

Статический момент площади обозначим S с индексом соответствующей оси:

(3.1)

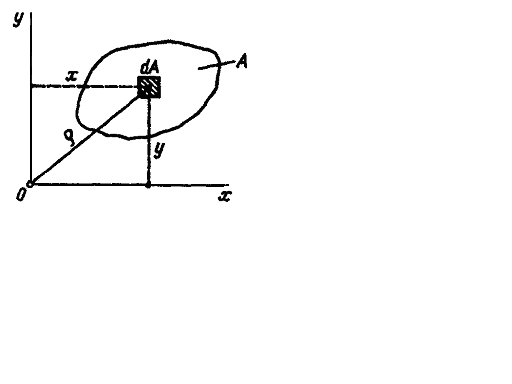
Рис. 3.1.

Формулы для определения координат центра тяжести площади фигуры:

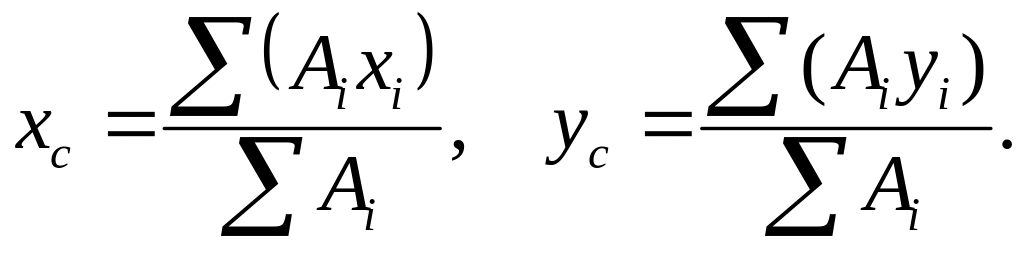(3.2)

Так как в формулах (3.2) под А можно понимать площадь dA элементарной площадки, то в пределе при dA, стремящемся к нулю, выражения, стоящие в числителях правых частей формул, будут представлять собой статические моменты площади фигуры относительно осей у и х, а , есть площадь А всей фигуры. Следовательно,

(3.3)

Единица статического момента площади  (единицы длины)³.

Статический момент площади фигуры может быть величиной положительной, отрицательной и равной нулю. Очевидно, что статический момент площади относительно оси, проходящей через центр тяжести площади фигуры (центральной оси), в том числе относительно оси симметрии фигуры, равен нулю.

В формулах для определения координат центра тяжести площади под А, можно понимать площади конечных частей фигуры, а под х и у  координаты центров тяжести этих частей (т. е. применять метод разбиения). Отсюда следует, что при определении статического момента площади сложной фигуры также можно применять метод разбиения, т. е. определять статический момент всей фигуры как алгебраическую сумму статических моментов отдельных ее частей:

(3.4)

где Si – статический момент площади каждой части фигуры.