Вариант № 3755934

1. C 2 . В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру и делит его в от­но­ше­нии 4:5, счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и

Ре­ше­ние.

Пусть плос­кость пе­ре­се­ка­ет ребро в точке Плос­кость се­че­ния пе­ре­се­ка­ет плос­кость по пря­мой па­рал­лель­ной сле­до­ва­тель­но, ис­ко­мое се­че­ние — па­рал­ле­ло­грамм (рис. 1).

 

 

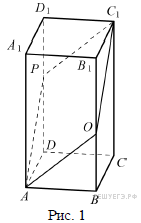
Тре­уголь­ни­ки и равны, сле­до­ва­тель­но,

 

 

Далее,

 

 

зна­чит,  — ромб со сто­ро­ной и диа­го­на­лью (рис. 2).

 

 

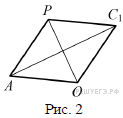
Тогда дру­гая диа­го­наль

 

 

Ответ:

2. C 2 . В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру и делит его в от­но­ше­нии 1:4, счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и

Ре­ше­ние.

От­ре­зок па­рал­ле­лен (точка при­над­ле­жит ребру ). Плос­кость се­че­ния пе­ре­се­ка­ет плос­кость по пря­мой па­рал­лель­ной сле­до­ва­тель­но, ис­ко­мое се­че­ние — па­рал­ле­ло­грамм (рис. 1).

 

Тре­уголь­ни­ки и равны, сле­до­ва­тель­но,

 

 

 

зна­чит,  — ромб со сто­ро­ной и диа­го­на­лью (рис. 2). Тогда диа­го­наль

 

 

Ответ:

3. C 2 . В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны ребер АВ и ВС и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если все ребра пи­ра­ми­ды равны 8.

Ре­ше­ние.

Пусть M — се­ре­ди­на AB, а N — се­ре­ди­на BC. Тогда пло­щадь се­че­ния равна пло­ща­ди тре­уголь­ни­ка SMN. Най­дем по­сле­до­ва­тель­но SM, MN и SN.

 

SM и SN — ме­ди­а­ны тре­уголь­ни­ков SAB и SBC со­от­вет­ствен­но. Т. к. эти тре­уголь­ни­ки рав­но­сто­рон­ние (по­сколь­ку все ребра пи­ра­ми­ды оди­на­ко­вой длины),

 

.

Най­дем те­перь MN из пря­мо­уголь­но­го тре­уголь­ни­ка MBN. В нем ка­те­ты равны 4. Ги­по­те­ну­за MN, по тео­ре­ме Пи­фа­го­ра, будет равна .

 

Те­перь най­дем пло­щадь рав­но­бед­рен­но­го тре­уголь­ни­ка SMN. Для этого про­ве­дем вы­со­ту SH, по тео­ре­ме Пи­фа­го­ра рав­ную , и вы­чис­лим пло­щадь:

 

 

.

 

Ответ: .

4. C 2 . Вы­со­та пра­виль­ной тре­уголь­ной пи­ра­ми­ды со­став­ля­ет от вы­со­ты бо­ко­вой грани Най­ди­те угол между плос­ко­стью ос­но­ва­ния пи­ра­ми­ды и её бо­ко­вым реб­ром.

Ре­ше­ние.

Пусть и

Тогда

 

 

Из тре­уголь­ни­ка на­хо­дим:

 

 

Тогда ис­ко­мый угол равен

 

Ответ:

5. C 2 . Дан куб Длина ребра куба равна Най­ди­те рас­сто­я­ние от се­ре­ди­ны от­рез­ка до плос­ко­сти

Вариант № 3757574

1. C 2 . В пра­виль­ной четырёхуголь­ной пи­ра­ми­де с вер­ши­ной сто­ро­ны ос­но­ва­ния равны а бо­ко­вые рёбра равны Най­ди­те пло­щадь се­че­ния пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку и се­ре­ди­ну ребра па­рал­лель­но пря­мой

Ре­ше­ние.

Пусть точка — се­ре­ди­на ребра От­ре­зок пе­ре­се­ка­ет плос­кость в точке В тре­уголь­ни­ке точка яв­ля­ет­ся точ­кой пе­ре­се­че­ния ме­ди­ан, сле­до­ва­тель­но, где — центр ос­но­ва­ния пи­ра­ми­ды. От­ре­зок па­рал­ле­лен и про­хо­дит через точку (точка при­над­ле­жит ребру — ребру ), от­ку­да

 

Четырёхуголь­ник — ис­ко­мое се­че­ние. От­ре­зок — ме­ди­а­на тре­уголь­ни­ка зна­чит,

По­сколь­ку пря­мая пер­пен­ди­ку­ляр­на плос­ко­сти диа­го­на­ли и четырёхуголь­ни­ка пер­пен­ди­ку­ляр­ны, сле­до­ва­тель­но,

 

 

Ответ:

2. C 2 . В пра­виль­ной тре­уголь­ной приз­ме сто­ро­ны ос­но­ва­ния равны 2, бо­ко­вые ребра равны 3, точка — се­ре­ди­на ребра Най­ди­те угол между плос­ко­стя­ми и

Ре­ше­ние.

Пря­мая пе­ре­се­ка­ет пря­мую в точке Плос­ко­сти и пе­ре­се­ка­ют­ся по пря­мой Из точки опу­стим пер­пен­ди­ку­ляр на пря­мую тогда от­ре­зок (про­ек­ция ), по тео­ре­ме о трех пер­пен­ди­ку­ля­рах, пер­пен­ди­ку­ля­рен пря­мой Угол яв­ля­ет­ся ли­ней­ным углом дву­гран­но­го угла, об­ра­зо­ван­но­го плос­ко­стя­ми и

Точка — се­ре­ди­на ребра по­это­му

Из ра­вен­ства тре­уголь­ни­ков и по­лу­ча­ем:

В рав­но­бед­рен­ном тре­уголь­ни­ке угол равен , вы­со­та яв­ля­ет­ся вы­со­той и бис­сек­три­сой, от­ку­да

Из пря­мо­уголь­но­го тре­уголь­ни­ка с пря­мым углом по­лу­ча­ем:

 

, тогда .

Ответ:

 

За­ме­ча­ние: Ответ может быть пред­став­лен и в дру­гой форме:

 

3. C 2 . В пра­виль­ном тет­ра­эд­ре най­ди­те угол между ме­ди­а­ной грани и плос­ко­стью

Ре­ше­ние.

Пусть, ребро тет­ра­эд­ра  — вы­со­та грани  — центр тре­уголь­ни­ка  — сред­няя линия тре­уголь­ни­ка Тогда зна­чит, и, сле­до­ва­тель­но,  — ис­ко­мый.

 

Кроме того, от­ку­да

Далее имеем:

Ответ:

4. C 2 . Плос­кость пе­ре­се­ка­ет два шара, име­ю­щих общий центр. Пло­щадь се­че­ния мень­ше­го шара этой плос­ко­стью равна Плос­кость па­рал­лель­ная плос­ко­сти ка­са­ет­ся мень­ше­го шара, а пло­щадь се­че­ния этой плос­ко­стью боль­ше­го шара равна Най­ди­те пло­щадь се­че­ния боль­ше­го шара плос­ко­стью

Ре­ше­ние.

Ре­ше­ние.

Се­че­ние шара плос­ко­стью — круг. Рас­смот­рим се­че­ние, про­хо­дя­щее через общий центр шаров и цен­тры кру­гов.

Обо­зна­че­ние цен­тра, точки ка­са­ния и точек пе­ре­се­че­ния по­верх­но­стей шаров с плос­ко­стя­ми и дано на ри­сун­ке.

— ра­ди­ус круга, по­лу­чен­но­го в се­че­нии мень­ше­го шара плос­ко­стью тогда — пло­щадь се­че­ния мень­ше­го шара плос­ко­стью .

— ра­ди­ус круга, по­лу­чен­но­го в се­че­нии боль­ше­го шара плос­ко­стью тогда — пло­щадь се­че­ния боль­ше­го шара плос­ко­стью

— ра­ди­ус круга, по­лу­чен­но­го в се­че­нии боль­ше­го шара плос­ко­стью Па­рал­лель­ные пря­мые и пер­пен­ди­ку­ляр­ны пря­мой Из пря­мо­уголь­ных тре­уголь­ни­ков по­лу­ча­ем: от­ку­да

Пло­щадь се­че­ния боль­ше­го шара плос­ко­стью

Ответ: 10.

5. C 2 . В пра­виль­ной тре­уголь­ной приз­ме сто­ро­ны ос­но­ва­ния равны 1, бо­ко­вые ребра равны 2, точка — се­ре­ди­на ребра Най­ди­те угол между плос­ко­стя­ми и