Задания С2

Вариант № 3742368

1. C 2 . В пра­виль­ной четырёхуголь­ной приз­ме ABCDA₁B₁C₁D₁ сто­ро­на ос­но­ва­ния равна 11, а бо­ко­вое ребро AA₁=7. Точка K при­над­ле­жит ребру B₁C₁ и делит его в от­но­ше­нии 8:3, счи­тая от вер­ши­ны B₁. Най­ди­те пло­щадь се­че­ния этой приз­мы плос­ко­стью, про­хо­дя­щей через точки B, D и K.

Ре­ше­ние.

Пусть L — точка, в ко­то­рой плос­кость се­че­ния пе­ре­се­ка­ет ребро C₁D₁. От­ре­зок KL па­рал­ле­лен диа­го­на­ли BD. Ис­ко­мое се­че­ние — тра­пе­ция BDLK (рис. 1). Плос­кость се­че­ния пе­ре­се­ка­ет ниж­нее ос­но­ва­ние по пря­мой BD, па­рал­лель­ной B₁D₁, зна­чит, KL па­рал­лель­но B₁D₁.

 

Тре­уголь­ни­ки LC₁K и D₁C₁B₁ по­доб­ны, сле­до­ва­тель­но,

 

 

Зна­чит,

 

В рав­ных пря­мо­уголь­ных тре­уголь­ни­ках DD₁L и BB₁K имеем зна­чит, тра­пе­ция BDLK рав­но­бед­рен­ная.

 

Пусть LH — вы­со­та тра­пе­ции BDLK, про­ведённая к ос­но­ва­нию BD (рис. 2), тогда:

 

 

 

Ответ:

2. C 2 . Точка — се­ре­ди­на ребра куба Най­ди­те угол между пря­мы­ми и

Ре­ше­ние.

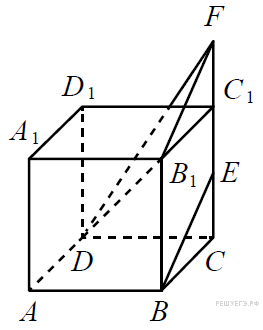При­мем ребро куба за Тогда Про­ведём через точку пря­мую, па­рал­лель­ную Она пе­ре­се­ка­ет про­дол­же­ние ребра в точке причём Ис­ко­мый угол равен углу (или смеж­но­му с ним).

В пря­мо­уголь­ном тре­уголь­ни­ке с пря­мым углом

 

В пря­мо­уголь­ном тре­уголь­ни­ке с пря­мым углом

 

В тре­уголь­ни­ке по тео­ре­ме ко­си­ну­сов

 

от­ку­да а тогда

Ответ: .

 

При­ме­ча­ние.

Ответ может быть пред­став­лен и в дру­гом виде:

 

 

3. C 2 . Дана пра­виль­ная четырёхуголь­ная пи­ра­ми­да MABCD, рёбра ос­но­ва­ния ко­то­рой равны . Тан­генс угла между пря­мы­ми DM и AL равен , L — се­ре­ди­на ребра MB. Най­ди­те вы­со­ту дан­ной пи­ра­ми­ды.

Ре­ше­ние.

Обо­зна­чим угол между и бук­вой . Пусть — вы­со­та пи­ра­ми­ды . Тогда — сред­няя линия тре­уголь­ни­ка , сле­до­ва­тель­но, . По­это­му . По усло­вию .

Ос­но­ва­ние — квад­рат со сто­ро­ной, рав­ной . Сле­до­ва­тель­но, , , . Далее, из пря­мо­уголь­но­го тре­уголь­ни­ка на­хо­дим:

 

 

Бо­ко­вое ребро , по­сколь­ку — сред­няя линия тре­уголь­ни­ка . Далее, из пря­мо­уголь­но­го тре­уголь­ни­ка на­хо­дим ис­ко­мую вы­со­ту пи­ра­ми­ды :

 

 

Ответ: 5.

4. C 2 . В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де SABCD, все ребра ко­то­рой равны 1, най­ди­те синус угла между плос­ко­стью SAD и плос­ко­стью, про­хо­дя­щей через точку A пер­пен­ди­ку­ляр­но пря­мой BD.

Ре­ше­ние.

Пусть точка  — центр ос­но­ва­ния, а  — се­ре­ди­на ребра По­сколь­ку и плос­кость пер­пен­ди­ку­ляр­на пря­мой Это зна­чит, что плос­кость и есть плос­кость, про­хо­дя­щая через точку пер­пен­ди­ку­ляр­но

Про­ве­дем от­рез­ки и Так как тре­уголь­ник пра­виль­ный, Так как тре­уголь­ник  — рав­но­бед­рен­ный, Сле­до­ва­тель­но, ис­ко­мый угол равен углу Най­дем сто­ро­ны тре­уголь­ни­ка

 

 

По тео­ре­ме ко­си­ну­сов:

 

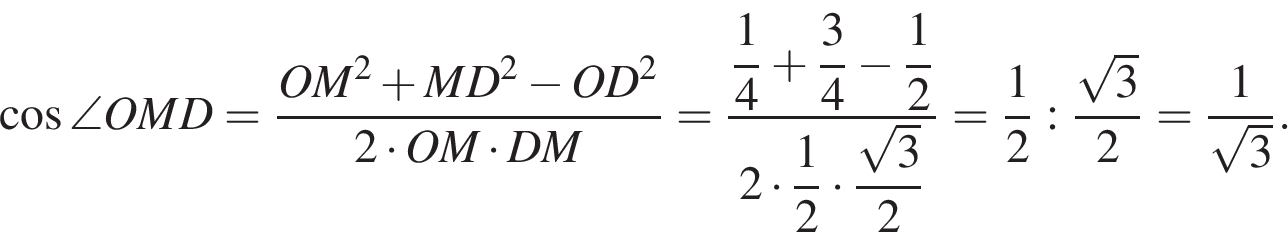
От­сю­да

Ответ:

При­ме­ча­ние.

Ре­ше­ние су­ще­ствен­но упро­ща­ет­ся, если за­ме­тить, что тре­уголь­ник — пря­мо­уголь­ный:

5. C 2 . Точка  — се­ре­ди­на ребра куба . Най­ди­те угол между пря­мы­ми и