Определение допускаемых изгибных напряжений.

Расчет зубьев на изгибную выносливость выполняют отдельно для зубьев шестерни и колеса, для которых вычисляют допускаемые напряжения изгиба по формуле

,

где − базовый предел изгибной выносливости зубьев, значения которого даны в таблице 4.

S_F - коэффициент безопасности, рекомендуют S_F = 1,55÷1,75 (см. табл.5);

К_FC - коэффициент реверсивности, учитывающий влияние двустороннего приложения нагрузки. При односторонней нагрузке К_FC = 1.

K_FL − коэффициент долговечности, методика расчета которого аналогична расчету K_HL (см. выше).

≥ 1

Примечание: 1- Значение базового числа циклов нагружения N_FO для всех сталей и значений твердости при испытании на изгибную усталость рекомендуется принимать равным 4·10⁶.

2 - Для стальных зубчатых колес с твердостью поверхности зубьев HB ≤ 350, а также для зубчатых колес с закалкой ТВЧ и обрывом закаленного слоя у переходной поверхности (в галтели) и зубчатых колес со шлифованной переходной поверхностью независимо от твердости и термообработки зубьев показатель кривой усталости m = 6, при этом 1 ≤ K_FL ≤ 2.0. Для стальных зубчатых колес с нешлифованной переходной поверхностью при твердости поверхности HB > 350 и чугунных колес m = 9, при этом 1 ≤ K_FL ≤ 1.6. Если N_FE ≥N_FO принимают K_FL = 1.

В рассматриваемом нами примере следует принять m=6.

3 – При расчете зубьев на изгиб имеет место отнулевой цикл изменении напряжений.

Допускаемые напряжения для проверки прочности зубьев при перегрузках.

В процессе работы редуктора возможна его работа с перегрузкой (пуск и т.д.). Однако, эта ситуация кратковременная, что позволяет вести расчет на прочность (выполнять проверку прочности) при повышенных значении допускаемых напряжений как на контактные давления, так и на изгиб.

Допускаемые контактные напряжения [σ_H]_max при расчете на контактную прочность при перегрузке моментом Т_max определяются в соответствии с таблицей 5 зависимостью

[σ_H]_max= [σ_H]_max2= 2.8·σ_T,

где [σ_H]_max2 соответствует колесу, прочность материала которого наименьшая из двух (шестерня и колесо).

Допускаемые напряжения изгиба при расчете на изгибную прочность определяются как для шестерни, так и для колеса.

[_F]_max1=2.74·HB₁

[_F]_max2=2.74·HB₂

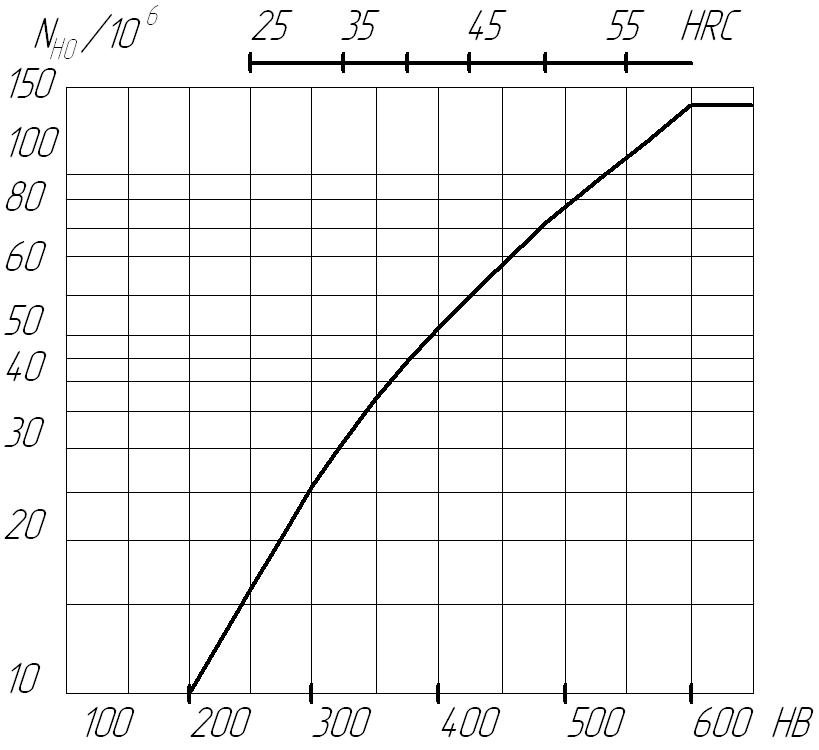
Рис. 5. Соотношение твердости рабочей поверхности и базового числа циклов

Расчет цилиндрической передачи редуктора.

После выбора материалов, режимов термообработки, расчёта крутящих моментов на валах, назначения передаточного числа передачи расчёт прямозубых и косозубых цилиндрических передач рекомендуется начинать с определения межосевого расстояния a_W, в мм.

Расчёт производят по следующей формуле:

_,

- вспомогательный коэффициент, имеющий размерность и полученный в результате выноса числового значения приведенного модуля упругости Е_пр из под корня, а также того, что в формуле использованы разные размерности физических величин: Т в Нм, а в мм, в МПа. В указанной формуле знак "+" принимают в расчётах передачи внешнего зацепления, а знак "–" – внутреннего зацепления. Для стальных прямозубых колес К_а = 490 (МПа)^1/3 , для косозубых К_а = 430 (МПа)^1/3 .

ψ_ba – относительная ширина колеса по межосевому расстоянию; (ψ_ba =b_W /a_W ) определяется по табл. 6 в соответствии со схемой расположения колес (см. рис.6), твердостью рабочих поверхностей колес.

Таблица 6. Относительная ширина колёс ψ_ba

Схема расположения колёс относительно опор	Твёрдость рабочих поверхностей зубьев
	менее НВ350	более НБ350
Симметричная	0,3...0,5	0,25...0,3
Несимметричная	0,25...0,4	0,20...0,25
Консольная	0,20...0,25	0,15...0,20

Большие значения ψ_ba целесообразно принимать для передач с постоянными или близкими к ним нагрузками.

В дальнейшем в расчетах может встретиться относительная ширина колес по диаметру ψ_bd = b_W / d_W1 , которую рассчитывают с учетом зависимости ψ_bd = ψ_ba (U±1) / 2 . Как и ранее знак “ + “ для внешнего зацепления, знак “ - “ для внутреннего зацепления. Типовые схемы расположения колес относительно опор приведены на рис. 6.

K_Hβ - коэффициент неравномерности нагрузки по длине контактной линии выбирают по кривым на графиках рис.7 а,б в соответствии с расположением зубчатых колёс передачи относительно опор, твёрдостью рабочих поверхностей зубьев и относительной шириной колес.

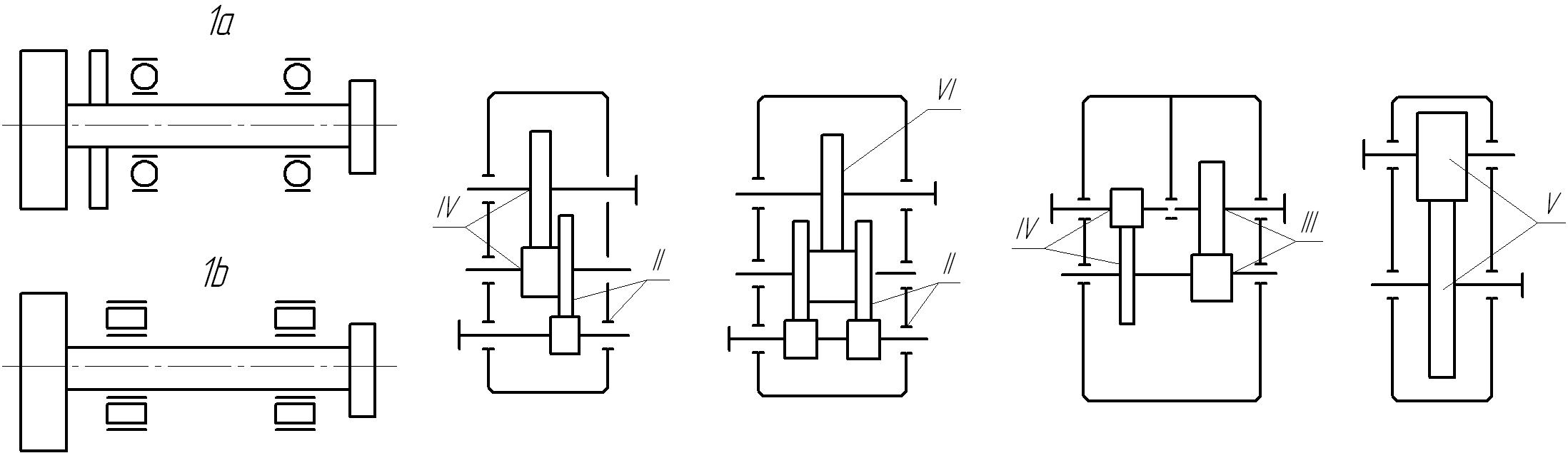
Рис. 6. Расположение зубчатых колёс передачи относительно опор

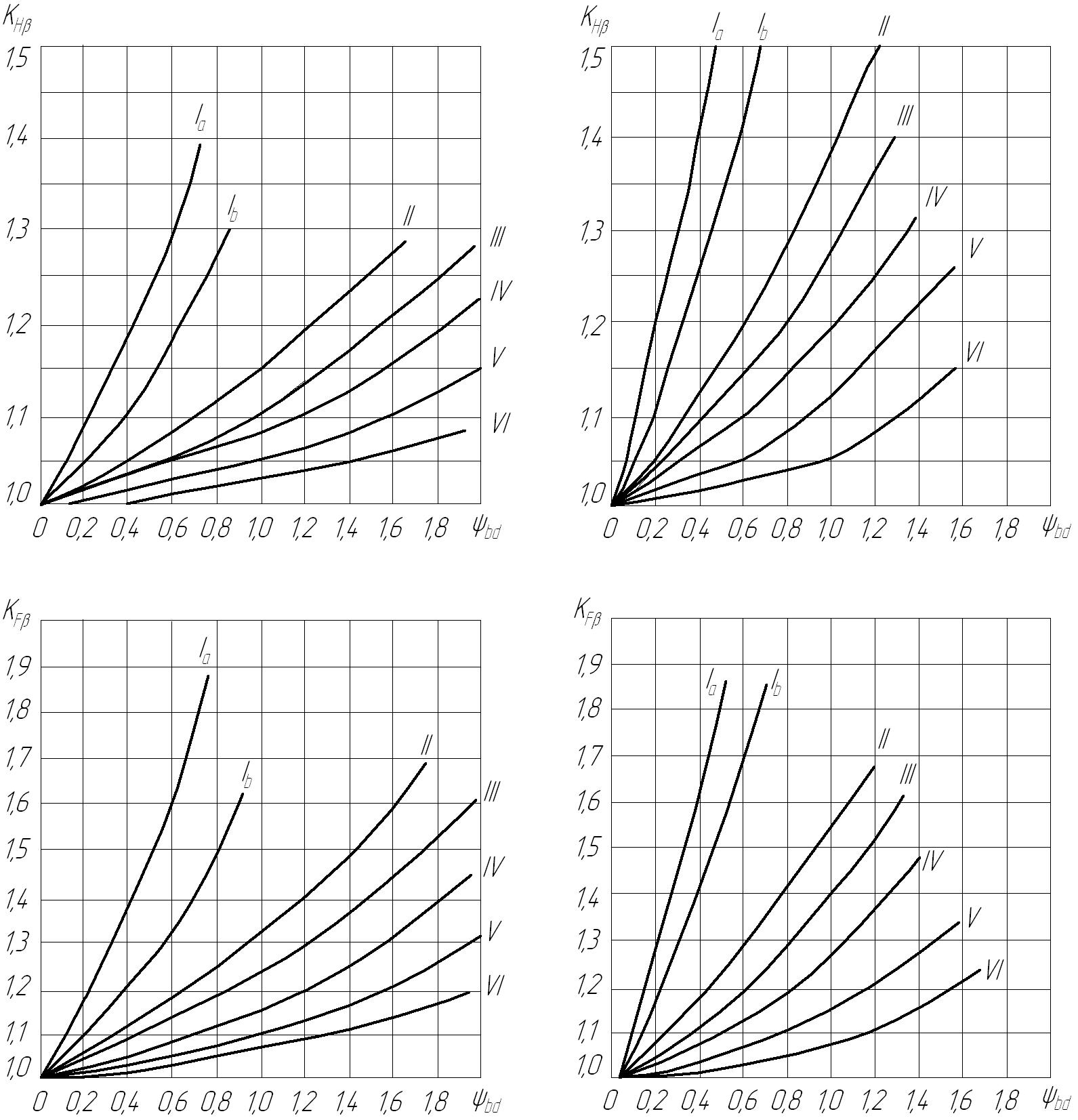
а) При HB₂ < 350 б) При HB₁ > 350 и HB₂ > 350

Рис. 7. Коэффициент неравномерности нагрузки

Примечание: для рассматриваемого нами редуктора принимается схема V.

Полученное значение межосевого расстояния a_w (мм) для нестандартных передач рекомендуется округлить до ближайшего большего значения по одному из рядов нормальных линейных размеров (см. табл. 7).

Таблица 7. Стандартные параметры зубчатых передач

Параметр	Относительная ширина зубчатых колес
ba	0,1	0,125		0,16		0,2	0,25		0,315		0,4		0,5		0,63			0,8		1,0		1,25
аw, мм	Межосевые расстояния
	1-й ряд			40		50	63		80		100		125		160			200		250		315
	2-й ряд												140		180			225		250		355
m, мм	Модули
	1-й ряд		1,0		1,25			2		2,5		3		4		5	6		8		10		12
	2-й ряд		1,125		1,375			1,75		2,25		2,75		3,5		4,5	5,5		7		9		11

Примечание. Для нестандартных редукторов расчетное значение а_w округляют по ряду Rа 40; 50; 63; 71; 75; 80; 85; 90; 95.100; 105: 112; 120; 125;130, далее через 10 до 260.