• Typy:

  • X … strukturní proměnné

    • Udávají úroveň jednotlivých procesů modelu (objem výroby obou druhů směsí)

  • d … doplňkové proměnné

    • doplňková proměnná má ekonomickou interpretaci

    • Udávají rozdíl mezi pravou a levou stranou omezujících podmínek (nevyužitá kapacita surovin)

    • rezerva, zbylé peníze

  • p … pomocné proměnné

    • Přidává se do požadavkových omezujících podmínek

    • Vždy s kladným znaménkem

    • Interpretace: kolik jednotek zbývá do splnění omezení

5. Uveďte a stručně popište typy omezujících podmínek V modelech lineárního programování. Ke každému typu uveďte příklad použití

• Exogenní (vnější) vazby systému

1. určení „ = “.

Pěstuji pšenici, ječmen a žito, a chci aby celková rozloha byla právě 140 ha => x1+x2+x3=140

2. kapacitní „ ≤ “;

omezení maximální kapacity (skladu, materiálu, času,…)

3. požadavkové„ ≥ “;

omezení minimálních požadavků kladených na model (minimální množství výrobků, které je potřeba vyrobit)

• Endogenní (vnitřní) vazby systému

1. Bilanční – x1 + x2 – x3 = 0

• Vyrovnaná bilance

• Bilance s neúplným krytím

• Bilance s přebytkem

2. Poměrové – Fi/ Fk

3. Poměrově‐přípustkové – delta / delta

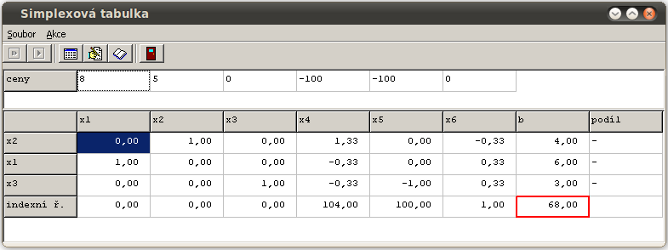
6. Prezentujte obecnou simplexovou tabulku. Jaké informace simplexová tabulka poskytuje?

• Koeficienty strukturních a doplňkových proměnných zapíšeme do vstupní simplexové tabulky

• První sloupec tabulky obsahuje proměnné, které jsou v bázi (struktura báze). V bázi jsou proměnné, jejichž vektory tvoří jednotkovou matici

• Další sloupce jsou nadepsány symboly všech proměnných, které se v úloze vyskytují

• Hodnoty bazických proměnných zjistíme v posledním sloupci tabulky (b - vektor pravých stran).

• Poslední řádek tabulky (indexní řádek – označený písmenkem Z)obsahuje anulovanou rovnici účelové funkce

• H odnotu účelové funkce v jednotlivých krocích zjistíme na průsečíku sloupce b a indexního řádku z

7. Popište účel, princip a postup provedení testu optimality V simplexové tabulce

• Abychom zjistili, jestli právě tyto bazické proměnné jsou optimálním řešením, které hledáme, musíme udělat test optimality

• Vytvoříme si pod tabulkou řádek (indexový řádek)

• Počítáme skalární součin Zj-Cj(cena)

• PRO MAX.	KLADNÉ
  PRO MIN.	ZÁPORNÉ

  Pod jednotkovým vektorem musí vyjít 0 => jinak počítám špatně

• Aby výsledek byl optimální, musí vyjít čísla v indexovém řádku=> Pro MAX.-> kladné, pro MIN. -> záporné

• Kdyby vyšlo optima, už dál nepočítám!

• Ale jelikož většinou optima nevyjde, musím počítat dál (určím si klíčový sloupec a vypočítám test přípustnosti=> klíčový řádek, přechod na nové řešení atd.)

8. Popište účel, princip a postup provedení testu přípustnosti V simplexové tabulce

• Poněvadž nám nevyšlo optimální řešení, musíme počítat dál dokud nevýjde

• V indexním řádku najdeme nejnižší číslo – tento sloupeček označíme jako klíčový.

• Proměnná, která je nadepsána v záhlaví klíčového sloupce se stane v dalším kroku základní, tedy vstoupí do báze

• Pak dělíme postupně pravou stranu (b) kladným číslem v klíčovém sloupci

• Ten řádek, kde vyjde podíl nejnižší, označíme jako klíčový řádek

• Proměnná v řádku, ke kterému přísluší nejnižší podíl z báze vystoupí.

• Úpravami musíme dostat do klíčového pole 1 a nad a pod něj 0, pomocí Gauss-Jordanovy eliminační metody. Klíčový pole= Pivot> číslo které mi protne klíčový sloupec a řádek

• Novou základní proměnnou zapíšeme do sloupce báze na místo vyloučené proměnné

• Tyto akce počítáme stále dokola, dokud nevyjde optimální řešení