14. Қабаттың ішкі шекарасындағы шарттар – ұңғы түбін модельдеу

2. Ішкі Г₂шекарасында:

- радиусы ұнғы түбіндегі тұрақты қысым

(8)

- тұрақты шығым. Бұл шарт Дарси заңы орындалғанда былай жазамыз:

(9)

немесе r=r болғанда; (10)

мұндағы F = - ұңғының шеткі беттерінің ауданы; h – қабат қалыңдығы.

-ұңғы түбіндегі айнымалы қысым

P(r болғанда, r=r (11)

-айнымалы шығым

болғанда r=r ; (12)

-ұңғының істен шығуы

0 болғанда r=r . (13)

№ 23 емтихан билеті

1. Жазықрадиалды фильтрация ағынының негізгі гидродинамикалық сипаттамаларын есептеу

2. Тұрақты дебитпен галерея жұмысқа жіберілген жағдайындағы СКДА әдісі (кері есеп).

3. Соколов – Гусейновтың орташалау әдісі

17. Жазықрадиалды фильтрация ағынының негізгі гидродинамикалық сипаттамаларын есептеу

Һ тұрақты қалыңдығы бар біртекті көлденең айналмалы қабат орталығында орналасқан радиусы r_с гидродинамикалық жетелдірілген ұңғыға қарай сығылмайтын сұйықтың ағып жатыр делік. Қоректену өнбойы ретінде қолданылатын радиусы r_к қабаттық сыртқы айналмалы шегінде Р тұрақты қысымы қалыптасқан, ал ұңғы түбіндегі Р қысым да тұрақты болады (сур.2).

Ұңғы қабырғасы - Р_с

r_c коректену аймағы - Р_к

r _k r_к

2-сурет. Бірөлшемді жазықрадиалды фильтрациялық ағынның сұлбасы

Дифференциалдық теңдеу бұл жағдайда былай болады:

0 (14)

r= алмастыруды енгізе отырып (14)-теңдікті сәйкесінше түрлендіргенде мынаған тең:

= 0 немесе = 0 (15)

(15)-теңдеуді келесі шекті шартпен есептейміз:

P=P_к болғанда r=r_к

P=P_с болғанда r=r_с (16)

(15)-формуланы екі рет интегралдан шығарып, (16)-формуланы ескере отырып қысымның таралу заңын табамыз:

(17)

Сүзілу (фильтрация) жылдамдығы:

= (18)

33. . Тұрақты дебитпен галерея жұмысқа жіберілген жағдайындағы скда әдісі (кері есеп).

А. Тұрақты шығымды Q=const қарастырайық.

Қозған аймақтағы қысым таралуының теңдеуі: (13)

Галерей шығымы (14)

(13) формуладағы қысым градиенті:

онда (15)

Орта есеппен алғандағы көлем бойынша қабат қысымы:

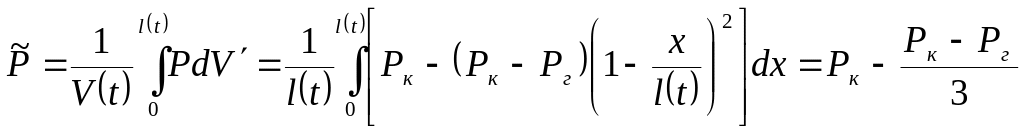
онда (16)

Материалдық баланс теңдеуін жазсақ:

осыдан (17)

(17) формуланы интегралдасақ және 0 – ден t – ға және 0- ден l- ға дейін шектесек:

(18)Қозған аймақтағы қысым таралуы: , 0 < x , (19)

Кейбір жағдайда ұңғының гидродинамикалық жетілмегендігі ұңғының жетілу коэффициенті көмегімен ескерімді: (4)

мұндағы Q– жетілдірілмеген ұңғыма шығымы, – жетілдірілген ұңғыма шығымы.

Ұңғының жетілдіру коэффициенті мен С шамасы бір-бірімен мына тәуелділікпен байланысқан: (5)

Бүкіл қозған аймақ бойынша серпімді режимінің дифференциалдық теңдеуіндегі қысымнан туындысы уақыт бойынша орташаланады және кейбір функциямен ауыстырылады . (1)

Оның мәні бастапқы және шекаралық шарттардан табылады. Сонда серпімді режимінің теңдеуі келесі түрге келеді: , (2)Тұрақты Q дебиті кезінде ұңғыға серпімді сұйықтың қалыптаспаған ағыны кезіндегі қысым таралуын анықтайық. Осы жағдайда түптегі және қозған аймақтың шекарасындағы шарттар (4)-(6) түрінде болады (12 дәрістегі).

(4)-(6) шарттар кезінде (2) теңдеуді r бойынша интегралдап табамыз; , (3)

(6) шарттан анықтаймыз; , (4)r²_c бар мүшелерді ескермей және (4) формуланы (3) формулаға қойып, табамыз

. (5)

Қозган аймақтың R(t) координатын анықтау үшін (5) тендікті t бойынша дифференциалдау, нәтижесін (1) қою және (4) өрнекті ескеру керек. Сонда аламыз

. (6)Сондықтан, қозған аймақтағы қысым таралуы (5) келесі түрде болады:

,

при . (7)

№ 24 емтихан билеті

1. Фильтрацияның серпімді режимі теориясының негізгі формуласы

2. Жазықрадиалды фильтрация ағынының негізгі гидродинамикалық сипаттамаларын есептеу

3. Көректену аймағы (КА) қашықтықта орналасқан, қабаттағы бір топ үңғыларға сұйықтықтың құйылуы