Задание 2

Доказать для произвольных множеств X,Y,W,Z справедливость (или несправедливость) следующих высказываний:

I² \ (X*Y) = [(I\X) * I ]∪ [ I*(I\Y)]

Теоретическая часть:

Кортеж (упорядоченное множество) – совокупность элементов, в которой каждый элемент занимает вполне определенное место.

Прямым (декартовым) произведением множества X на множество Y – называется упорядоченное множество A, состоящее из таких и только таких элементов (x,y), что x принадлежит X, а y принадлежит Y.

;

Практическая часть

1. 

Метод взаимного включения:

Пусть =M, а =N , тогда, если мы докажем, что MN, и NM то равенство верно.

1. MN

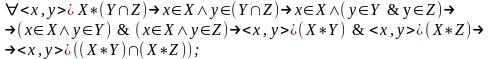
Прямое включение доказано.

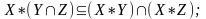
2. NM

Обратное включение доказано

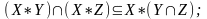
Значит

2. I ² \ (X*Y) = [(I \X) * I ]∪ [ I*(I\Y)]

Метод взаимного включения:

Пусть I ² \ (X*Y) =M, а [(I \X) * I ]∪ [ I*(I\Y)]=N , тогда, если мы докажем, что MN, и NM то равенство верно.

1. MN

2. NM

Задание 3

Доказать или опровергнуть, что для множеств А,В,С, где причем справедливы высказывания:

Теоретическая часть:

Операция проектирования справедлива для множеств, элементами которых являются кортежи одинаковой длины.

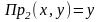
Операция проектирования множества, состоящего из кортежей - операция выделения первых, вторых и т. д. компонент кортежей и образование из них нового множества.

Практическая часть

Докажем с помощью метода взаимного включения:

Пусть =M, а =N , тогда, если мы докажем, что MN, и NM то равенство верно.

1. MN

Прямое включение доказано.

2. NM

Обратное включение доказано.

Значит

Докажем с помощью метода взаимного включения:

Пусть =M, а =N , тогда, если мы докажем, что MN, и NM то равенство верно.

1. MN

т. е. прямое включение не верно

2. NM

т. е. обратное включение не верно

Задание 4

Верно ли для всех А, В, С утверждение: если А и В , то В=Ø

Теоретическая часть:

Высказывания, построенные из простых высказываний с помощью логических операций ( ), называются логическими формулами.

Логическое значение формулы однозначно определяется логическими значениями входящих в нее простых высказываний.

Практическая часть:

Метод эквивалентных преобразований:

(1) т.к А

(2) т.к В

По закону де Моргана:

Подставляем во (2) выражение вместо А выражение (1):

По закону де Моргана:

Применяем дистрибутивный закон:

Т.к и имеем

(по свойству пустого множества)

Задание 5

Задайте отношение:

1. Антирефлексивное, нетранзитивное, связное;

2. Рефлексивное, симметричное, несвязное;

3. Полного порядка (вполне упорядоченное).

Теоретическая часть:

Отношением 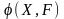на произвольном множестве 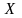называется пара .

- область задания, - график.

- область определения.

- область значений.

Способы задания отношений:

1. теоретический

2. матричный

3. графический

Отношение :

- рефлексивное, если: ;

-антирефлексивное, если: ;

- симметричное, если: ;

- несимметричное, если: ;

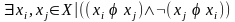- антисимметричное, если: ;

- транзитивное, если: ;

- нетранзитивное, если транзитивность не выполняется для всех или для некоторых ;

- связное, если

Отношение φ=(Х,F) называется отношением нестрогого (частичного) порядка (рис.2.41), если обладает следующими тремя свойствами:

Практическая часть:

1. Антирефлексивное, нетранзитивное, связное;

Теоретическое представление:

Матричное представление:

	1	2	3	4	5	6
1		1	1		1
2			1	1	1	1
3
4	1		1		1	1
5			1
6	1		1		1

Графическое представление:

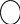
2. Рефлексивное, симметричное, несвязное

Теоретическое представление:

Матричное представление:

	1	2	3	4	5	6
1	1			1		1
2		1	1		1
3		1	1
4	1			1
5		1			1
6	1					1

Графическое представление:

3. Полного порядка (вполне упорядоченное).

Теоретическое представление:

Матричное представление:

	1	2	3	4	5	6
1	1	1				1
2		1		1	1	1
3	1	1	1	1
4	1			1	1
5	1		1		1	1
6			1	1		1

Графическое представление: