- •Классификация дисперсных систем.
- •1.3.1. Классификация по дисперсности
- •1.3.2. Классификация по агрегатному состоянию фаз
- •1.3.3. Классификация по форме частиц дисперсной фазы
- •1.3.4. Классификация по соотношению размеров частиц дисперсной фазы
- •1.3.5. Классификация по характеру межфазного взаимодействия
- •1.3.6. Классификация по кинетическим свойствам дисперсной фазы и дисперсной среды
- •. Классификация поверхностных явлений
- •Поверхностное натяжение
- •Поверхностное натяжение
. Классификация поверхностных явлений
GS=S Роль интенсивного фактора (обобщенной силы) играет , а роль экстенсивного (обобщенной координаты) – S. Снижение поверхностной энергии двумя путями: за счет уменьшения поверхностного натяжения и за счет уменьшения поверхности раздела. В связи с этим все поверхностные явления делятся на две группы.
Рассмотрим классификацию поверхностных явлений в соответствии с объединенным уравнением I и II начал термодинамики. Запишем его для поверхностного слоя:
|
(2.1) |
В
уравнении (2.1) приращение свободной
энергии Гиббса представлено как
алгебраическая сумма приращений
различных видов энергии: тепловой,
механической, поверхностной, химической
и электрической. Выделим из всей суммы
поверхностную энергию
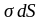 (где
(где
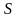 – поверхность). Поверхностная энергия
может превращаться в другие виды энергии,
и эти превращения сопровождают
возникновение различных поверхностных
явлений. Так, например, превращение
поверхностной энергии в энергию Гиббса
(
– поверхность). Поверхностная энергия
может превращаться в другие виды энергии,
и эти превращения сопровождают
возникновение различных поверхностных
явлений. Так, например, превращение
поверхностной энергии в энергию Гиббса
(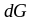 )
сопровождает изменение реакционной
способности с изменением дисперсности,
что количественно описывается уравнением
Томсона-Кельвина. В результате превращения
в теплоту (
)
сопровождает изменение реакционной
способности с изменением дисперсности,
что количественно описывается уравнением
Томсона-Кельвина. В результате превращения
в теплоту (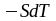 )
происходит смачивание и адгезия, что
количественно оценивается уравнением
Дюпре. Превращение в механическую
энергию (
)
происходит смачивание и адгезия, что
количественно оценивается уравнением
Дюпре. Превращение в механическую
энергию (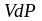 )
связывается с капиллярными явлениями.
Основой теории капиллярных явлений
служит уравнение Лапласа. Поверхностное
явление, называемое адсорбцией,
сопровождает превращение поверхностной
энергии в химическую (
)
связывается с капиллярными явлениями.
Основой теории капиллярных явлений
служит уравнение Лапласа. Поверхностное
явление, называемое адсорбцией,
сопровождает превращение поверхностной
энергии в химическую (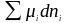 )
и оценивается уравнением Гиббса. И,
наконец, превращение в электрическую
энергию (
)
и оценивается уравнением Гиббса. И,
наконец, превращение в электрическую
энергию (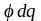 ),
приводит к электрическим явлениям
(уравнение Липпмана).
),
приводит к электрическим явлениям
(уравнение Липпмана).
Поверхностное натяжение
Термодинамическое определение поверхностного натяжения вытекает из уравнения (2.1). при постоянных T, P, n и q имеем:
|
(2.2) |
Поверхностное натяжение – есть частная производная от энергии Гиббса по величине поверхности раздела фаз при постоянных значениях температуры, давления, числа молей компонентов и заряда.
.Пповерхностное натяжение можно определить как частную производную от любого термодинамического потенциала Например, для внутренней энергии:
|
(2.3) |
|
(2.4) |
Поверхностному натяжению можно дать и энергетическую характеристику. Рассмотрим молекулярные силы по границе жидкости с собственным паром (рис. 2.2). На молекулу внутри жидкости действуют силы притяжения со стороны соседних таких же молекул. Поэтому в глубине жидкости межмолекулярные силы скомпенсированы и их равнодействующая Р не равна 0.
На поверхности молекула испытывает притяжение практически только со стороны одной фазы – жидкости, поэтому равнодействующая межмолекулярных сил Р не равна 0 и направлена в глубь жидкости. Эта равнодействующая называется внутренним давлением. У молекул поверхностного слоя остается нереализованная способность к взаимодействию, которая будет характеризовать свободную поверхностную энергию.
Работа образования единицы новой поверхности и представляет собой поверхностное натяжение. Эта работа эквивалентна увеличению свободной поверхностной энергии при увеличении поверхности на единицу:
|
(2.5) |
Иными словами: поверхностное натяжение – это удельная свободная поверхностная энергия. Измеряется в системе СИ в Дж/м2=нм/м2=н/м. Строго говоря, поверхностное натяжение является удельной поверхностной энергией только для индивидуальных веществ
Поверхностное натяжение можно представить и как работу, необходимую для разрыва столбика вещества, состоящего из одной фазы с поперечным сечением в 0,5 см2.
Чем
сильнее межмолекулярные связи в данном
теле, тем больше его поверхностное
натяжение. Наименьшим значением
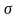 обладают газы, затем идут жидкости,
причем, чем выше полярность жидкости,
тем выше ее поверхностное натяжение.
Еще больше поверхностное натяжение у
твердых тел.
обладают газы, затем идут жидкости,
причем, чем выше полярность жидкости,
тем выше ее поверхностное натяжение.
Еще больше поверхностное натяжение у
твердых тел.
Билет 4. . Классификация поверхностных явлений
GS=S Роль интенсивного фактора (обобщенной силы) играет , а роль экстенсивного (обобщенной координаты) – S. Снижение поверхностной энергии двумя путями: за счет уменьшения поверхностного натяжения и за счет уменьшения поверхности раздела. В связи с этим все поверхностные явления делятся на две группы.
Рассмотрим классификацию поверхностных явлений в соответствии с объединенным уравнением I и II начал термодинамики. Запишем его для поверхностного слоя:
|
(2.1) |
В уравнении (2.1) приращение свободной энергии Гиббса представлено как алгебраическая сумма приращений различных видов энергии: тепловой, механической, поверхностной, химической и электрической. Выделим из всей суммы поверхностную энергию (где – поверхность). Поверхностная энергия может превращаться в другие виды энергии, и эти превращения сопровождают возникновение различных поверхностных явлений. Так, например, превращение поверхностной энергии в энергию Гиббса ( ) сопровождает изменение реакционной способности с изменением дисперсности, что количественно описывается уравнением Томсона-Кельвина. В результате превращения в теплоту ( ) происходит смачивание и адгезия, что количественно оценивается уравнением Дюпре. Превращение в механическую энергию ( ) связывается с капиллярными явлениями. Основой теории капиллярных явлений служит уравнение Лапласа. Поверхностное явление, называемое адсорбцией, сопровождает превращение поверхностной энергии в химическую ( ) и оценивается уравнением Гиббса. И, наконец, превращение в электрическую энергию ( ), приводит к электрическим явлениям (уравнение Липпмана).

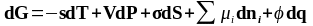
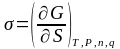
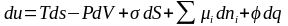

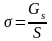 или
или