Енергія, функція Лагранжа та Гамільтона[ред. • ред. Код]

Кінетична енергія гармонічного осцилятора задається виразом

.

Потенціальна енергія гармонічного осцилятора задається виразом

.

Відповідно, вважаючи величину   узагальненою координатою, функція Лагранжа гармонічного осцлятора записується

.

Узагальнений імпульс

Функція Гамільтона

.

Вимушені коливання[ред. • ред. Код]

Під дією зовнішньої періодичної сили із частотою, яка не обов'язково збігається із власною частотою гармонічного осцилятора, осцилятор здійснює гармонічні коливання, аплітуда яких визначається величиною зовнішньої сили і співвідношенням зовнішньої частоти й власної частоти осцилятора.

Вимушені коливання гармонічного осцилятора із частотою   під дією сили з частотою  описуються рівнянням

,

де   — амплітуда зовнішньої сили.

Частинний розв'язок цього рівняння, який описує вимушені коливання має вигляд

.

Гармонічний осцитор під дією зовнішньої сили здійснює гармонічні коливання з амплітудою  . При   амплітуда вимушених коливань прямує до нескінченості. Це явище називається резонансом.

Гармонічний осцилятор із згасанням коливань[ред. • ред. код]

При врахуванні сил тертя чи супротиву іншого роду, який призводить до дисипації енергії осцилятора й перетворенні її в тепло, рівняння гармонічного осцилятора змінюються. Зокрема дуже поширений випадок, коли сили супротиву пропорційні швидкості зміни величини  . Тоді рівняння гармонічного осцилятора набирає вигляду

.

Такі коливання затухають із часом згідно із законом

.

Вимушені коливання гармонічного осцилятора із згасанням[ред. • ред. код]

При дії періодичної зовнішньої сили навіть при затуханні для осцилятора встановлюються гармонічні коливання із амплітудою, яка залежить від прикладеної сили, співвідношення частот, а також від величини затухання.

Амплітуда вимушених коливань із врахуванням затухання визначається формулою

.

Це скінченна величина при всіх частотах зовнішньої сили.

Формули для розрахунку частот гармонічних осциляторів[ред. • ред. код]

Математичний маятник при невеликому початковому відхиленні від вертикалі здійснює гармонічні коливання з частотою

,

де g — прискорення вільного падіння, l — дожина маятника.

Тіло масою m на пружині із жорсткістю k, є гармонічним осцилятором з частотою

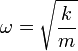
Коливальний контур є гармонічним осцилятором, із частотою

,

де L — індуктивність, C — ємність.

Гармонічний осцилятор у квантовій механіці[ред. • ред. код]

Детальніше див. Квантовий осцилятор.

Спектр власних значень і власні функції[ред. • ред. код]

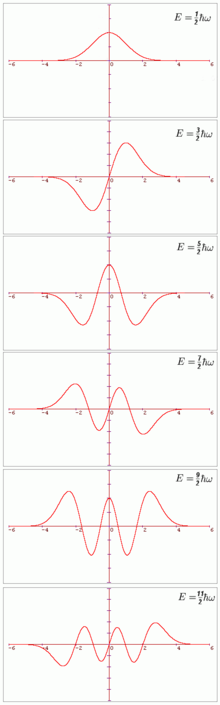
Хвильові функції перших шести станів із квантовими числами від n = 0 до 5. На осі ординат відкладена узагальнена координата

Гамільтоніан гармонічного осцилятора отримується заміною у функції Гамільтона імпульсу   на 

.

Спектр гармонічного осцилятора знаходиться із стаціонарного рівняння Шредінгера й задається формулою

.

Тут   — квантове число, яке пробігає значення від нуля до нескінченості. Енергетичні рівні гармонічного осцилятора еквідистантні. Характерною особливістю гармонічного осцилятора є те, що навіть у основному стані гармонічний осцилятор має відмінну від нуля енергію

.

Ця найнижча енергія називається енергією нульових коливань.

Власні функції гармонічного осцилятора, які відповідають квантовому числу   задаються формулами

,

де  , а   — поліноми Ерміта.

При парному   власні функції гармонічного осцилятора парні, при непраному — непарні. Гамільтоніан гармонічного осцилятора комутує із оператором заміни   на   (оператором парності), а тому має спільні власні функції з цим оператором.