Тема 2.1 Кінематика. Основні поняття кінематики.

План лекції

1. Види руху точки по заданій траєкторії в залежності від її прискорення.

2. Визначення параметрів руху точки по заданій траєкторії для будь-якого виду руху.

3. Поступальний рух твердого тіла.

4. Оберти тіла навкруг непорушної осі.

1. Види руху точки по заданій траєкторії в залежності від її прискорення.

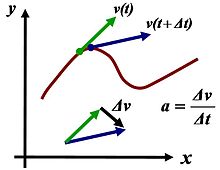
Прискорення - це зміна швидкості. У будь-якій точці траєкторії

прискорення задається не тільки зміною абсолютного значення швидкості, а й її напрямку. Прискорення визначається як границя відношенні приросту швидкості до інтервалу часу, за який цей приріст відбувся.

Види руху:

Рівномірний рух – це рух тіла, при якому прискорення не змінюється ні за величиною, ні за напрямком.

Нерівномірний рух - якщо точка в рівні проміжки часу проходить нерівні шляхи.

Рівномірно-змінний рух – рух, при якому за рівні проміжки часу швидкість змінюється на одну і ту ж величину.

2.Визначення параметрів руху точки по заданій траєкторії для будь-якого виду руху

Координатний спосіб завдання руху точки

Положення в просторі рухомої точки визначається трьома координатами в декартовій системі координат. Ці координати задаються як функції часу:

(1)

Залежності (1) називаються рівняннями руху точки в декартових координатах.

Якщо рух точки відбувається в площині ХУ, то задаються тільки два рівняння руху:

При прямолінійному русі точки досить задати одне рівняння руху: , якщо прийняти, що вісь х збігається з прямою, по якій рухається точка.

Швидкість точки являє собою вектор, що характеризує швидкість і напрям руху точки в даний момент часу.

При завданні руху точки рівняннями (1) проекції швидкості на осі декартових координат дорівнюють:

Модуль швидкості

(2)

Напрямок швидкості визначається напрямними косинусами:

Якщо рух точки задається в площині ХУ, то;

При прямолінійному русі по осі х:

Характеристикою швидкості зміни швидкості є прискорення а. Прискорення точки одно похідною від вектора швидкості по часу:

При завданні руху точки рівняннями (1) проекції прискорення на координатні осі дорівнюють:

Модуль прискорення:

(3)

Напрямок прискорення визначається напрямними косинусами

Якщо рух точки задається в площині ХУ, то:

При прямолінійному русі по осі Х

Природний спосіб завдання руху точки:

Вважається, що рух точки задано природним способом, якщо вказані її траєкторія і закон зміни криволінійної координати. Рівняння називається законом руху точки по траєкторії. При цьому на траєкторії вказується початок відліку, а також позитивний напрямок відліку координати s у вигляді стрілки .

Модуль швидкості точки визначається за формулою

Вектор швидкості V спрямований по дотичній до траєкторії в бік стрілки , якщо , і в протилежну сторону, якщо .

Прискорення точки визначається як векторна сума дотичного і нормального прискорень точки:

Модуль дотичного прискорення визначається за формулою

Вектор дотичного прискорення направлений по дотичній до траєкторії в бік стрілки , якщо , і в протилежну, якщо .

Модуль нормального прискорення визначається за формулою

де - ρ радіус кривизни траєкторії в даній точці.

Вектор нормального прискорення завжди спрямований по головній нормалі в бік центру кривизни траєкторії.

Модуль повного прискорення