Тема 1.6 Центр ваги. Методика розв’язання задач.

Визначення положення центру ваги перерізів

План лекції

1. Координати центру тяжіння тіла.

2. Методика рішення задач.

3. Приклад задачі

1. Теоретичне обґрунтування

Центром тяжіння тіла називають точку всередині тіла (або поза ним), відносно якої сума моментів сил тяжіння, які діють на окремі частини тіла, дорівнює нулю.

Положення центра тяжіння будь-якого тіла можна знайти, розбиваючи тіло на частини більш простої форми і визначаючи центри прикладання рівнодійної сил тяжіння, які діють на ці частини. Наприклад. тонка однорідна пластинка

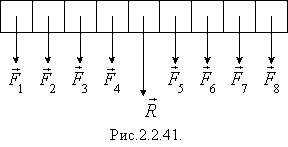
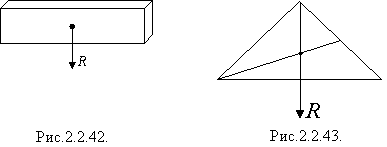
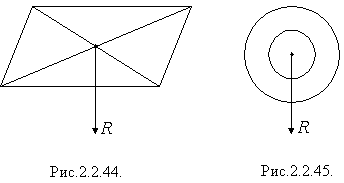
Розіб'ємо пластинку на багато малих рівних між собою смужок. На кожну з них діє сила тяжіння - всі ці сили рівні між собою. Складаємо по дві сили, рівновіддалені від середини смужок. Рівнодійні будь-яких двох таких сил прикладено в середині смужки. Звідси випливає, що центр тяжіння однорідної тонкої пластинки знаходиться в її середині. Так само можна встановити, що центр тяжіння однорідного прямокутного стрижня знаходиться в його середині (рис.2.2.42), трикутника - в точці перетину його медіан (рис.2.2.43), паралелограма - в точці перетину його діагоналей (рис.2.2.44), однорідного кільця - в його геометричному центрі (рис.2.2.45)

Наведені приклади доводять, що якщо тіло має центр симетрії, то центр тяжіння збігається з центром симетрії. Якщо тіло має вісь симетрії, то його центр тяжіння лежить на цій осі. Якщо тіло має площину симетрії, то його центр тяжіння лежить в цій площині.

В будь-якій точці фізичного тіла діє сила тяжіння. Через невеликі розміри тіл, що розглядаються, у порівнянні з відстанню їх до центру Землі, сили тяжіння розглядають як систему паралельних сил. Рівнодіючу сил тяжіння точок тіла називають силою тяжіння, а точку її прикладання – центром тяжіння (або центром ваги тіла)

Координати центру тяжіння тіла визначають за формулами:

;

Координати центру тяжіння тіла, що складається з площин, визначають за формулами:

;

Добуток площі тіла на відстань від центра тяжіння цього тіла до осі зветься статичним моментом тіла відносно осі

;

2. Методика розв’язання задач.

Визначення положення центра ваги складного перерізу (використовувати таблиці сортаменту прокатних профілів).

1. Розбиваємо переріз на профілі прокату, позначаємо цифрами 1,2,3,..n

2. Вказуємо центри ваги кожного профілю С1, С2,С3,…n

3. Обираємо систему координатних осей.

Усі перерізи мають одну вісь перерізу, тому рекомендується одну з координатних осей сполучати з нею. Другу вісь координат направляють перпендикулярно першій так, щоб вона перетинала центри тяжіння однієї з фігур. Другу вісь можливо направити так, щоб вона пройшла крізь нижню (крайню) точку перерізу. В першому випадку рішення будуть більш простими.

4. Визначаємо з відповідних таблиць сортаменту площі профілів А1, А2, А3,...n і, використовуючи розміри, знаходимо координати їхніх центрів ваги х1, х2, х3, …n і у1,у2, у3,…n відносно обраних осей координат (координати у_с = 0, тому що вісь X збігається з віссю симетрії). По черзі для кожного профілю: відстань від 0 центральних вісей до центру вісей С1, потім від 0 до С2, і т.д. відстань відповідно осі Х – відстані Х1, Х2, Х3,…n.

5. Визначаємо повну площу перетину А (сума всіх А1,А2,А3…n) (см²)

6. Знаходимо статичний момент перетину S_y = А₁х₁+А₂х₂+А₃х₃+А₄х₄ (см³)

S_х = А₁у₁+А₂у₂+А₃у₃+А₄у₄(см³)

Якщо вісь X збігається з віссю симетрії, S_х = 0,

7. Визначаємо координати центра ваги

х_с =S_у/A

у_с =S_х/A

Якщо вісь X збігається з віссю симетрії, то координата у_с = 0

8. Отже точка С має координати (х_с; y_с)

Наносимо знайдений центр ваги на малюнок перерізу.