Пример №6
После года хранения на складе в среднем 10% аккумуляторов выходит из строя. Определить вероятность того, что после года хранения из 12 аккумуляторов годными окажутся 10 аккумуляторов.
Решение:
Событие
А- наудачу взятый аккумулятор после
года хранения годный. Вероятность
Р(А)=р=0,9;
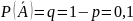; р=0,9=const
каждого n=12
аккумуляторов.
Следует
определить вероятность
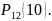Применим формулу Бернулли:
Получаем:
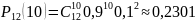
Пример №7
Дан закон распределения случайной величины Х
Х |
-1 |
0 |
2 |
Р |
0,2 |
|
0,3 |
Найти
,
М(Х), D(X),
P(-0.5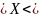
1)
,F(X).
Построить график F(X).
Решение:
Так
как
,
то 0,2+
+0,3=1,
откуда
=0,5
и закон распределения принимает вид
Х |
-1 |
0 |
2 |
Р |
0,2 |
0,5 |
0,3 |
Найдем
математическое ожидание случайной
величины Х, используя формулу M(X)=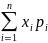
.
М(Х)=-1*0,2+0*0,5+2*0,3=0,4
Для
нахождения дисперсии воспользуемся
формулой D(X)=M(
.
При этом M(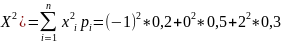
=1,4.
Тогда D(X)=1,4-0,16=1,24.
Составим функцию распределения F(X). По определению F(X) находим:
если
х
-1,
то
Р(Х
х)=0;
если -1 х 0, то F(X)=Р(Х х)=Р(Х=-1)=0,2;
если 0 х 2, то F(X)=Р(Х х)=Р(Х=-1)+Р(Х=0)=0,2+0,5=0,7;
если х 2, то F(X)=Р(Х х)=Р(Х=-1)+Р(Х=0)+Р(Х=2)=0,2+0,5+0,3=1.
Итак,
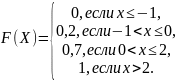
Строим график этой функции:
У
1
0,7
0,2
-1 2 Х
Найдем
вероятность Р(-0,5
)
попадания случайной величины Х в заданный
интервал по формуле:
Р(a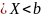
)=F(b)-F(a)
Получим
Р(-0,5 )= F(1)-F(-0,5)=0,7-0,2=0,5.