Образец выполнения некоторых заданий. Пример №1

Решить дифференциальное уравнение,

- уравнение с разделяющимися переменными.

Разделим переменные:

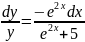
Интегрируя, получим общий интеграл:

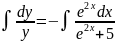
или

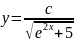
Пример №2

Решить уравнение .

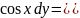Перепишем уравнение в виде 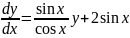или

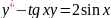
Уравнение линейно относительно у. Решим его методом подстановки y=uv, тогда .

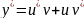Приведем уравнение к виду:

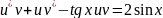или

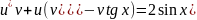
Найдем функцию v(x), решая уравнение . Тогда для нахождения функции получим уравнение . Решаем первое уравнение:

или ; ; ; .

;

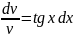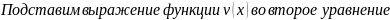
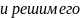
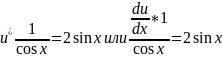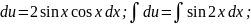
Перемножая u(x) и v(x) , получим общее решение заданного уравнения: .

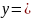Пример №3

Найти частное решение уравнения , удовлетворяющее начальным условиям

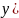
Сначала решим соответствующее однородное уравнение

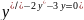
Его характеристическое уравнение имеет корни 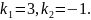Значит, - общее решение однородного уравнения.

Частное решение неоднородного уравнения будем искать в виде , так как в правой части исходного уравнения коэффициентом при показательной функции служит многочлен нулевой степени и 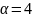не является корнем характеристического уравнения.

Дифференцируя два раза, получим

Подставляем 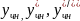в исходное уравнение и приходим к равенству (16А-8А-3А)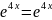 или 5А=1. Таким образом, 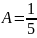. Следовательно, общее решение данного уравнения

Для нахождения 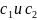воспользуемся начальными условиями:

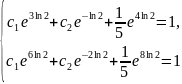
или

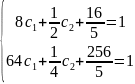
Отсюда,

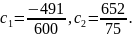
Пример №4

Исследовать функцию xy на экстремум.

Решение

а) Находим частные производные первого порядка

,

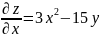б) Воспользовавшись необходимыми условиями экстремума, находим стационарные точки:

откуда

в) Находим частные производные второго порядка в точках .

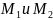В точке

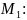
=0, ,

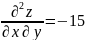
В точке :

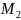=30, ,

Тогда значение дискриминанта в точке

, то есть в точке экстремума нет.

Значение дискриминанта в точке

.

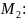
Следовательно , в точке заданная функция имеет минимум.

Величина этого минимум .

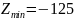Пример №5

Вероятность сдать каждый из трех экзаменов сессии на отлично для студента М равна соответственно 0,8; 0,7 и 0,75. Найти вероятность того, что студент сдаст на отлично:

а) все три экзамена;

б) два экзамена;

в) хотя бы один экзамен.

Решение:

Обозначим :

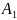- студент сдаст первый экзамен на отлично;

- студент сдаст второй экзамен на отлично;

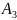- студент сдаст третий экзамен на отлично;

Этим событиям противоположные соответственно

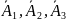
По условию:

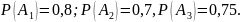
Тогда .

а) Обозначим А-студент сдаст на отлично все три экзамена, то есть и первый, и второй, и третий экзамены. Тогда .

Вероятность события А найдем по теореме умножения для независимых событий:

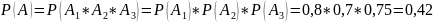
б) Обозначим В- студент сдаст какие- либо два из трех экзаменов на отлично. Тогда В=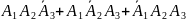 . Вероятность события В найдем, применяя сначала теорему сложения для несовместных событий, а затем теорему умножения для независимых событий:

)

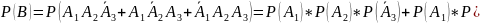0,8*0,7*0,25+0,8*0,3*0,75+0,2*0,7*0,75=0,425

в) Обозначим С- хотя бы один экзамен из трех студент сдаст на отлично. Тогда противоположное ему событие - ни один экзамен студен на отлично не сдаст.

По следствию из теоремы сложения вероятностей получим:

Р(С)=1-Р(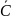 )=1-Р( )=1-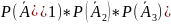

P(C)=1-0,2*0,3*0,25=1-0,015=0,985