Тема 3. Постановка задачи принятия решений в условиях неопределенности

Изучаемые понятия и термины

Модель принятия решений. Понятие неопределенности условий. Понятие альтернатив. Графические и математические модели. Аппарат линий уровня.

Методические указания

В результате изучения данной темы студент должен получить предс-тавление о содержании задачи принятия решения. Любая модель принятия решений основывается на выборе предпочтительного варианта действий из множества альтернатив. Особенностью логистики является то, что решения имеют оптимизационный характер. Связано это с тем, что в той или иной форме логистические операции осуществляются на любом предприятии с большей или меньшей эффективностью.

Для принятия решения основанного на приемах и методах системного анализа логистической системы следует реализовать следующие процедуры:

1. Определить множество всех возможных внешних ситуаций не зависящих от лица принимающего решения (ЛПР)), которые влияют на экономический результат соответствующих решений в рамках анализируемого проекта (сделки, предложения и т.п.). Указанный набор ситуаций должен представлять собой полную группу событий. Последнее означает, что должны выполняться следующие два условия: одновременное наступление любых двух событий такой полной группы невозможно и одно из событий полной группы наступит обязательно.

2. Составить перечень всех альтернативных решений, которые требуется анализировать, и для которых экономический результат будет зависеть от реализованной «внешней» ситуации.

3. Определить ожидаемые доходы ( ) - для случаев, когда будет принято некое решение, выбранное ( ) из множества указанных выше анализируемых альтернатив, а внешняя, не зависящая от ЛРП, ситуация сложится такая, которая соответствует событию . Эти доходы представляют соответствующими конечными результатами выручки или прибыли (по желанию менеджера). Они оформляются в виде матрицы , которую называют матрицей полезностей:

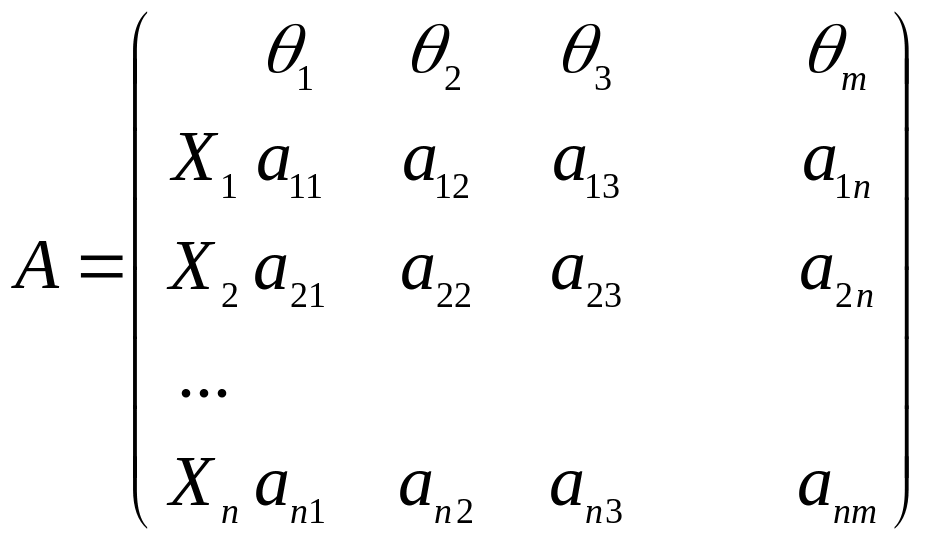
4. Выбрать альтернативу из множества возможных решений.

Рис. 2. Формализация УТ и АУТ

	точки возможных решений ЛПР
	УТ, АУТ
V, U	переменные, определяющие принятие решений
,	Значения переменных в УТ

Если же значимое число альтернативных решений неизвестно, их следует оценивать и выбирать на основании линий уровня.

При изучении данного понятия следует обратить внимание на понятия утопической и антиутопической точек (УТ и АУТ) (рис. 2).

Утопическая точка – это условная точка в пространстве доходов, координаты которой представлены наилучшими (наибольшими) элементами по соответствующим столбцам матрицы полезностей.

Аналогично, антиутопическая точка – это точка в пространстве доходов, координаты которой представлены наихудшими (наименьшими) элементами, соотносимыми с каждым случайным событием полной группы (по соответствующим столбцам матрицы полезностей).

Все возможные (отличные от ) альтернативные решения, для которых ни одна из координат не будет меньшей, чем соответствующая координата у решения X₀ (U₀ либо V₀), образуют конус предпочтений по отношению к X₀.

Один из формальных подходов, позволяющий проиллюстрировать возможности «раскрытия» неопределённостей указанного типа, состоит в привлечении так называемого аппарата линий уровня. С помощью таких линий можно характеризовать отношение конкретного ЛПР к неопределённости экономического результата в соответствующем поле полезностей.

Пусть требуется сравнить альтернативное решение с некоторой другой альтернативой, которая в ситуации дает экономический результат , худший, чем результат решения (рис. 3).

Отметим сначала один «крайний» случай, когда такая альтернатива, сравниваемая с X₀, будет представлена именно точкой . Тогда указанное альтернативное решение X₀ будет предпочтительнее, чем альтернатива .

Рис. 3. Иллюстрация понятия линя уровня

где

- данная величина потерь в случае наступления события ;

- требуемая ЛПР компенсация соответствующих возможных потерь в случае наступления события ;

- альтернатива, эквивалентная решению X₀.

С другой стороны, для любого конкретного ЛПР всегда найдется такая «своя» точка , лежащая на указанной выше линии, которая будет предпочтительней для ЛПР при выборе из множества альтернатив.