Запитання для самоконтролю
Лінійні форми:
1. Лінійною формою називається_____________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
2. Які з наведених форм є лінійними:
а)
в)
б)
г)
_________________________________________________________________
_________________________________________________________________
3. Лінійні функціонали – це _________________________________________
_________________________________________________________________
_________________________________________________________________
4.
Загальний вид лінійної форми
-вимірного
простору
_________________________________________________________________
_________________________________________________________________
5. Формула зв’язку між коефіцієнтами лінійної форми в різних базисах __________________________________________________________________
_________________________________________________________________,
де_______________________________________________________________
6. Зв’язний простір – це
_________________________________________________________________
_________________________________________________________________
7. Лінійна
форма виду
,
називається
______ ___________________________________________________________
8. Зв’язано-лінійна форма – це ______________________________________
_________________________________________________________________
Білінійні форми:
1. Білінійною формою називається
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
2. Навести приклади білінійних форм (вказати стовпчик або рядок коефіцієнтних форм).
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
3. Загальний вигляд білінійної форми в -вимірному лінійному просторі.
_________________________________________________________________
_________________________________________________________________
4. Формула зв’язку між коефіцієнтами білінійної форми при зміні базису.
_________________________________________________________________
_________________________________________________________________
5. Ермітова білінійна форма – це
_________________________________________________________________
_________________________________________________________________,
а матриця_________________________________________є ермітовою.
6. Симетрична білінійна форма –
це_______________________________________________________________
_________________________________________________________________
Квадратичні форми:
1. Якщо в білінійній формі__________________________________________,
то одержимо квадратичну форму.
Навести приклади:
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
2. Нехай
в базисі
квадратична форма має матрицю
,
то
____________________,
де ______________________________________
3. Квадратична форма канонічна – це _________________________________
_________________________________________________________________
_________________________________________________________________
4. Симетрична матриця, складена з ___________________________________
_________________________________________________________________
називається матрицею квадратичної форми.
5. Полярою квадратичної форми називається___________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
6.
Квадратична матриця
називається__________________________,
якщо
,
тобто________________________________________________.
Задачі на доведення:
Довести, що для будь-якої ненульової лінійної функції
,
заданої в
-мірному
лінійному просторі
,
існує канонічний базис, в якому ця
функція записується в канонічному
вигляді
,
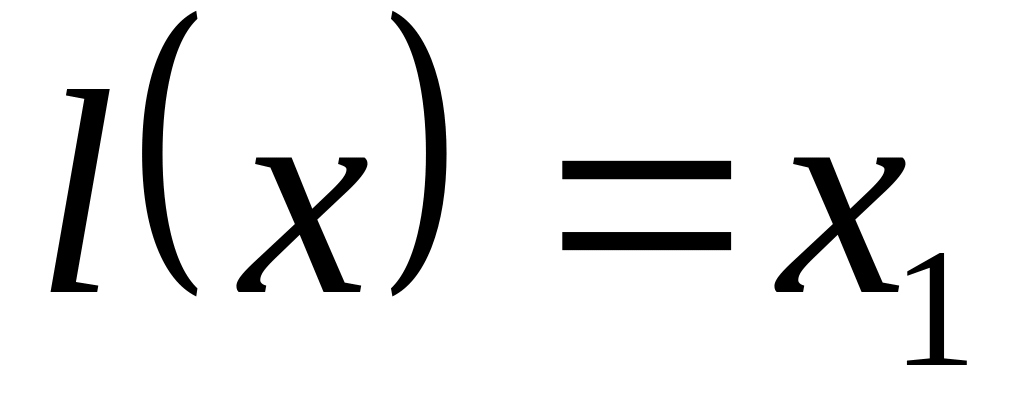де
- перша координата вектора
в цьому базисі.
Вказівка:
Знайти базис
,
для якого
2. Довести,
якщо добутокдвох лінійних функцій,
заданий на лінійному просторі
(не обов’язково
скінченному), тотожно рівний нулю, тобто,
для будь-якого
,
то принаймні одна з цих функцій тотожно
рівна нулю.
Вказівка:
Припустимо,
що
і розглянути вектор
.
3. Довести,
якщо дві лінійні функції
і
на лінійному просторі
(не обов’язково
скінченному) мають одне і те ж ядро
,
то
,
де
- число, відмінне від нуля.
Вказівка:
Для ненульової функції взяти вектор
,
що не належить
,
покласти
,
використавши, що для будь-якого вектора
,
що не належить
,
будь-який вектор
одночасно подається у вигляді
.
4. Довести, що - ненульова лінійна функція на лінійному просторі (не обов’язково скінченному). Довести, що:
а) ядро
функції
,
тобто множина всіх векторів
,
для яких
,
якщо максимальний лінійний підпростір,
тобто
не міститься в підпросторі
,
відмінному від
і
;
б) для
будь-якого вектора
,
не лежить в
,
будь-який вектор
відповідно подається у вигляді
,
де
.
Вказівка:
покласти,
що
.
Задачі на розв’язання:
1. Знайти нормальний вигляд в області дійсних чисел квадратичних форм:
а)
;
б)
;
в)
;
г)
;
д)
.
Відповіді:
а)
;
б)
;
в)
;
г)
;
д) .
2. Наступні квадратичні форми звести до канонічного вигляду з цілими коефіцієнтами за допомогою невиродженого лінійного перетворення з раціональними коефіцієнтами і знайти вираження нових невідомих через старі:
а)
;
б)
;
в)
.
Відповіді:
а)
б)
в)
3. Для
наступних квадратичних форм знайти
невироджене лінійне перетворення, що
призводить
у форму
(шукане перетворення визначене
неоднозначно):
а)
б)
в)
Відповіді:
а)
б)
в)
