Приклади розв’язання задач

Лінійні форми

Приклад 1. Лінійна форма у просторі функція виду

, де - деякі числа, а - координати вектора у фіксованому базисі.

Перевіримо, що ця функція задовольняє загальному означенню лінійної форми на довільному лінійному просторі.

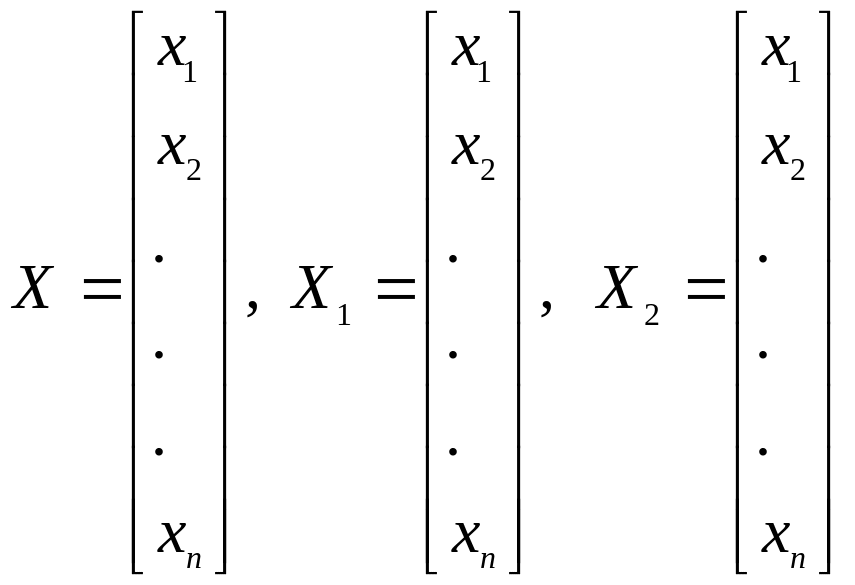
Нехай , а ­ – стовпці з координат векторів в даному базисі. Оскільки лінійна залежність векторів рівносильна такій же лінійній залежності між стовпцями з їх координат, то , або по визначеній дії із стовпцями ,

Звідси отримаємо:

.

Що й потрібно було довести.

На проміжку неперервних на функцій визначимо числову функцію рівністю , де - фіксована неперервна на функція.

Легко перевірити, що задана так функція є лінійною, тобто задовольняє умові:

Підставимо в кожну функцію її значення в деякій точці , тобто покладемо: .

Очевидно, що лінійній комбінації двох функцій зіставляється така ж комбінація їх значень .

Метод Лагранжа

Приклад 1. Знайти нормальний вигляд квадратичної форми

і неособливе лінійне представлення , що приводить до цього вигляду.

Матриця заданої квадратичної форми в базисі е має вигляд 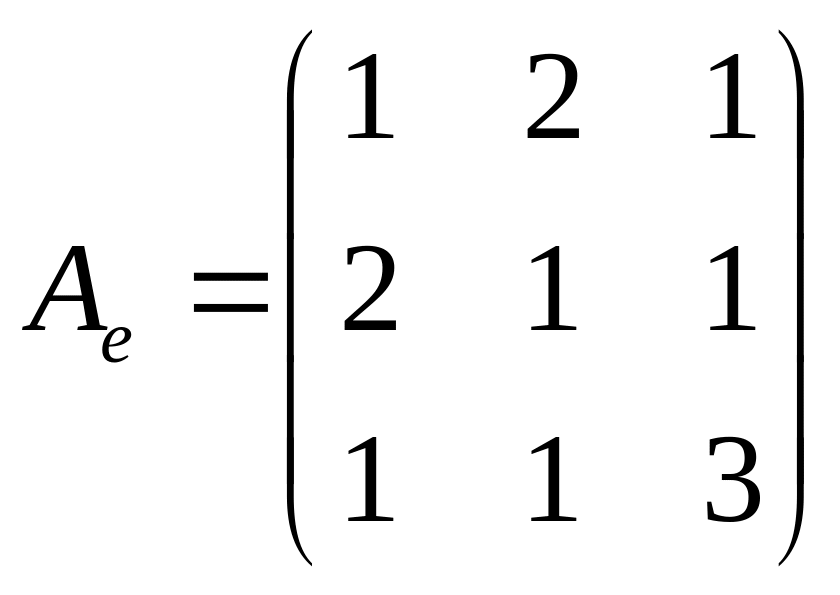. Виділимо з усіх членів квадратичної форми доданки, що містять координату (виділимо повний квадрат):

.

Одержимо: .

З останніх трьох доданків виділимо знову повний квадрат відносно змінної .

Отже, .

Позначимо , , .

Одержимо нормальний вигляд квадратичної форми:

(4.1)

Щоб знайти матрицю переходу Т від початкового базису , в якому вектор х має координати , або в якому квадратична форма має вигляд (4.1), розглянемо формули перетворення координат, як координатне розписування матричної форми формули перетворення координат.

, де - матриця обернена до матриці переходу.

Використовуючи позначення записуємо:

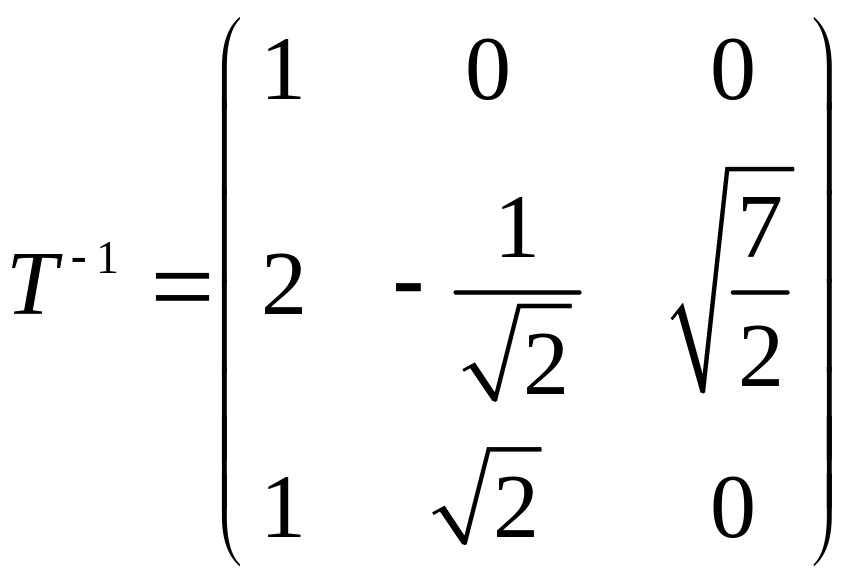матриця обернена до і є матриця переходу від базиса до базиса , тобто . Знаходимо її.

Шукана матриця переходу .

За допомогою матриці можна скласти шукане лінійне перетворення:

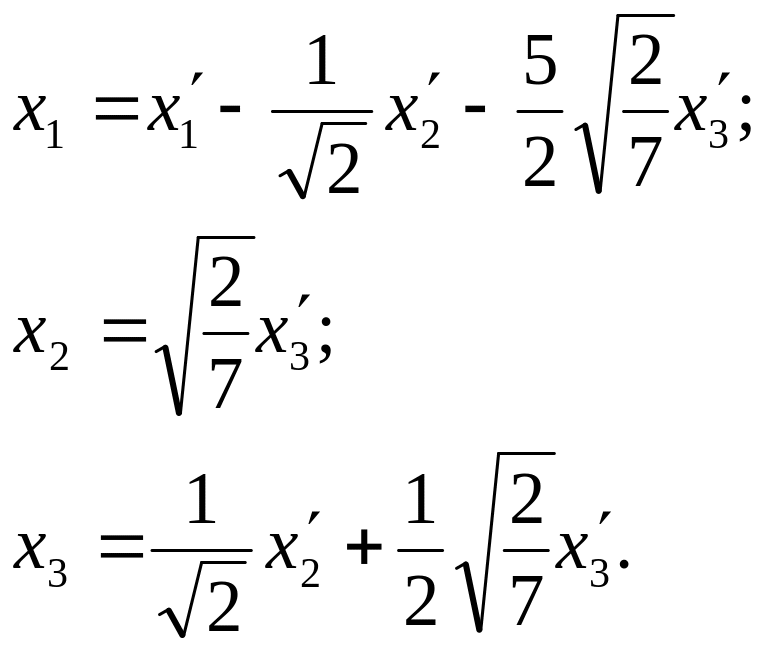
Запишемо канонічний базис:

і здійснимо перевірку за формулою: .

Приклад 2. Знайти канонічний базис і нормальний вигляд квадратичної форми .

Матриця заданої квадратичної форми:

.

В розглядуваній квадратичній формі немає жодного члена з квадратом координат, а тому, щоб одержати хоча б одну змінну в квадраті запровадимо спочатку лінійне перетворення

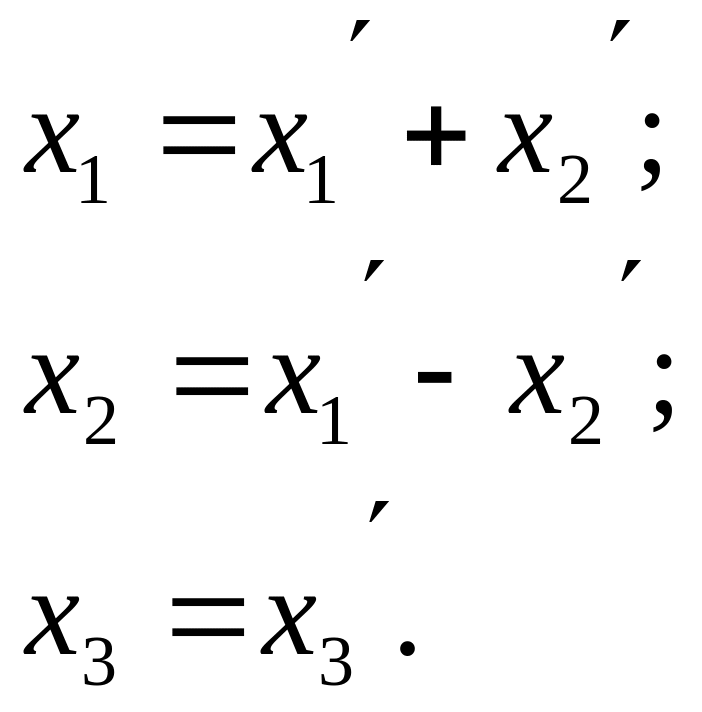
Щоб знайти матрицю переходу скористаємось формулою

,

очевидно, що .

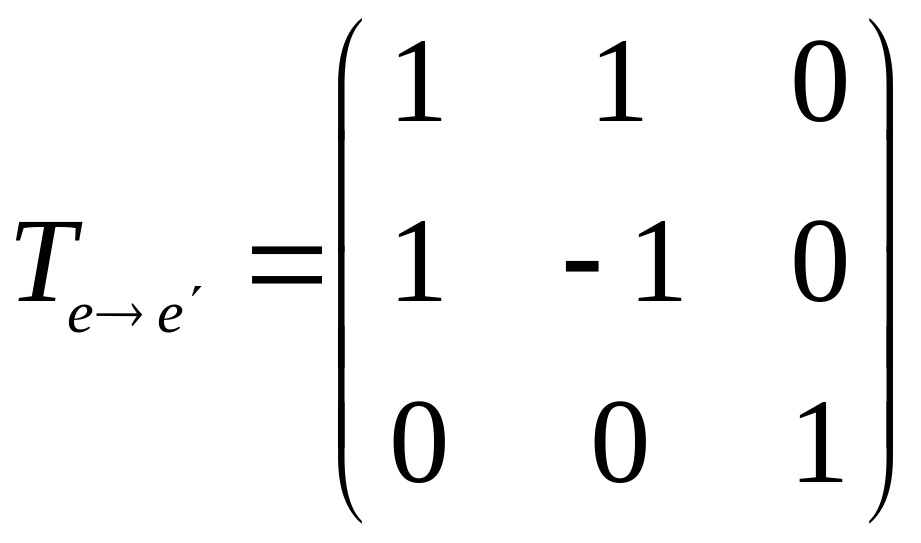Канонічний вид квадратичної форми в базисі : .

Матриця цієї квадратичної форми: .

Застосуємо метод Лагранжа для зведення до нормального виду.

.

Нехай

.

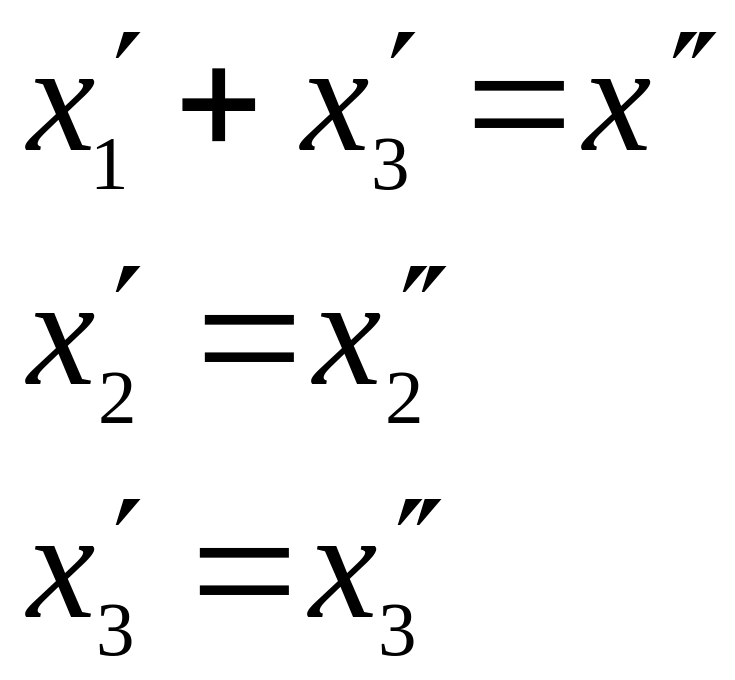Матриця квадратичної форми в базисі .

Знаходимо матрицю переходу від базису до базису : . Звідси

Використовуючи формулу , ,

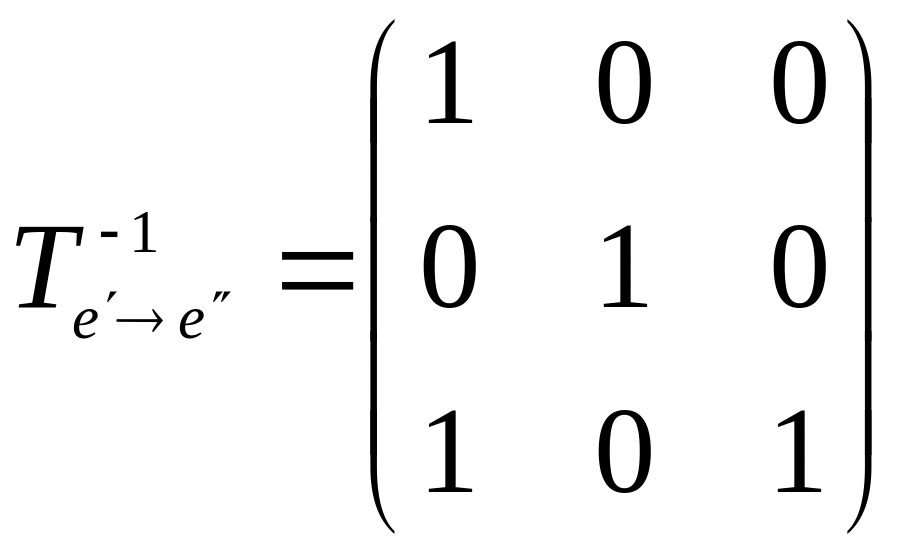одержуємо: .

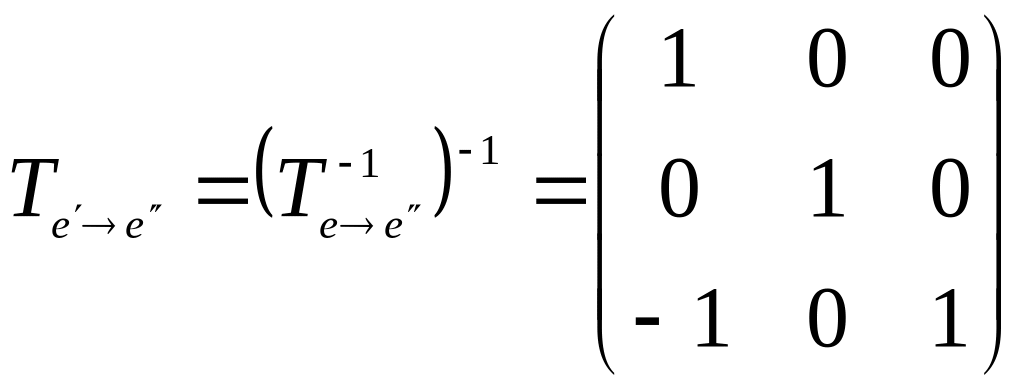Матриця переходу від координат до координат :

.

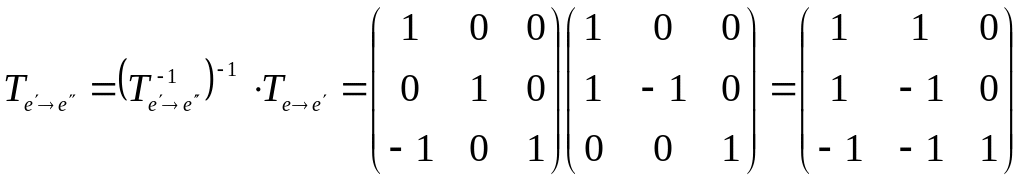Отже, канонічний базис складається із векторів

а формули перетворення координат:

.

Перевірку здійснюємо використовуючи формули зв’язку між матрицями квадратичної форми.

Приклад 3. Квадратична функція дана в базисі . Записати цю квадратичну функцію в базисі : .

Розв’язання. .

Новий базис матиме вигляд:

, .

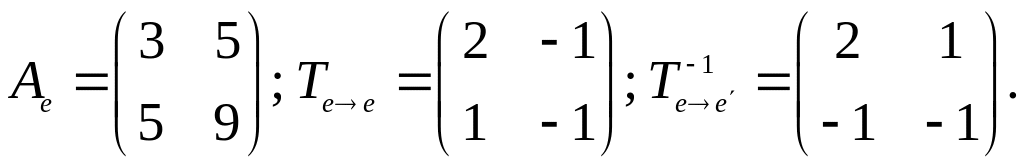
Щоб знайти матрицю квадратичної форми в базисі скористаємось формулою зв’язку між матрицею квадратичної форми в різних базисах:

(4.2)

.

Отже, в базисі квадратична форма має вигляд: .

Знайдемо вираження змінної через змінну :

.

Приклад 4. Методом Лагранжа звести квадратичну форму до нормального виду:

Матриця заданої квадратичної форми має вигляд:

.

Покладемо що:

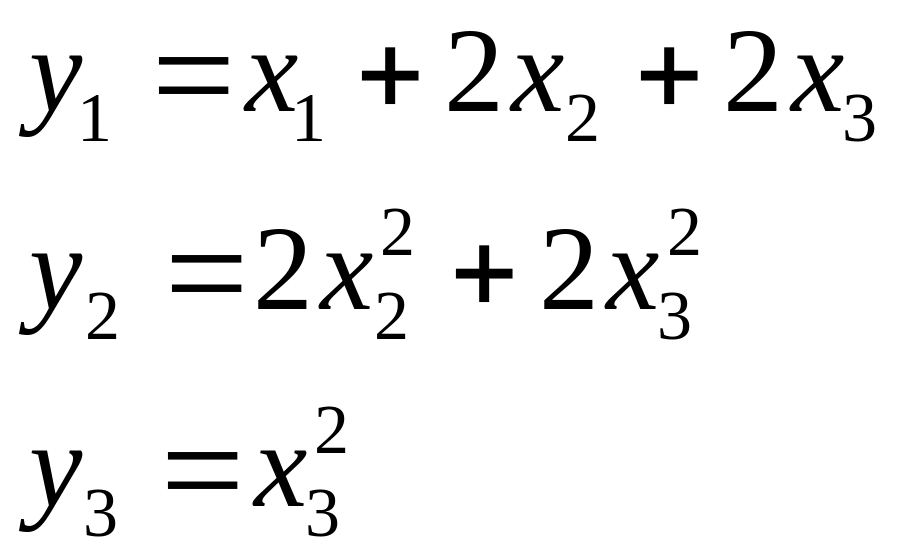
і одержимо нормальний вид заданої квадратичної форми:

.

Її матриця .

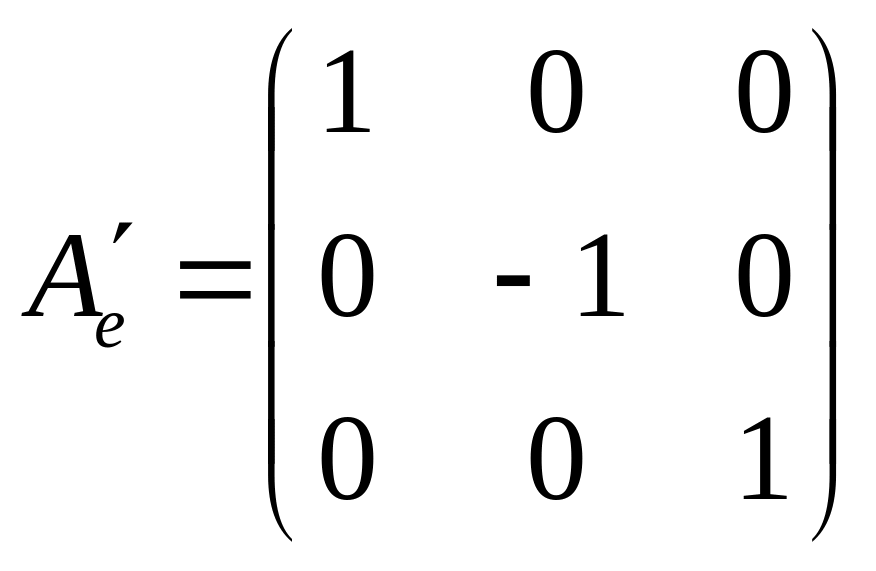Знаходимо :

,

.

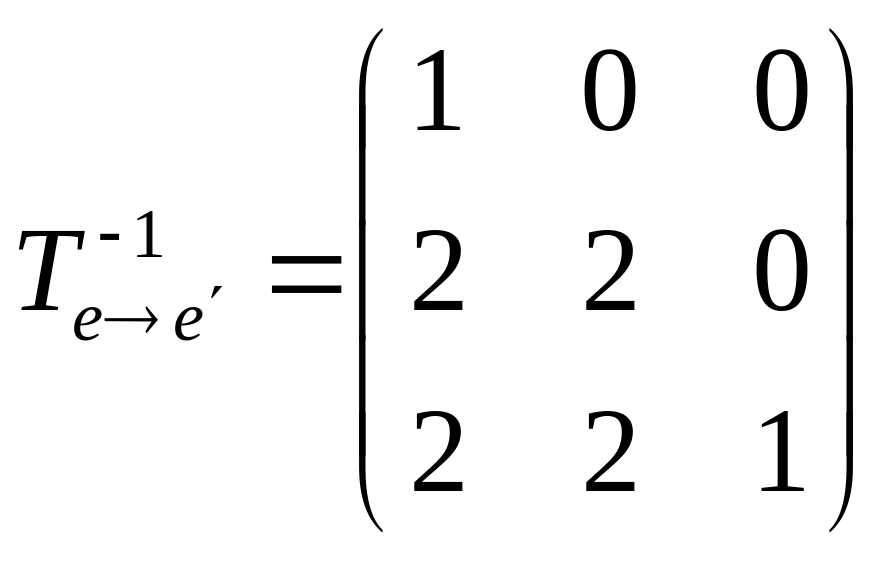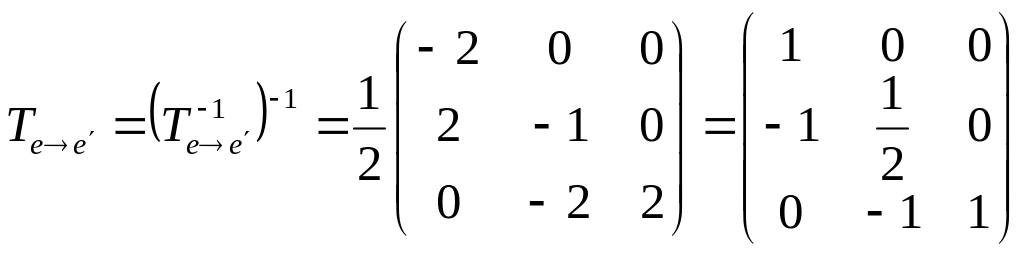Базис, в якому квадратична форма має нормальний вигляд:

Перевірка.

І спосіб. .

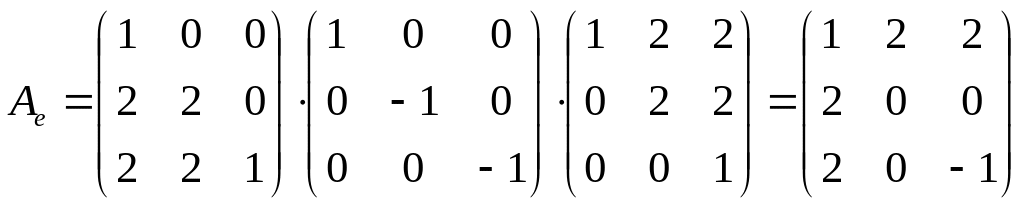ІІ спосіб. Знаючи, що . знайдемо . Розв’язуючи матричне рівняння, маємо .

.

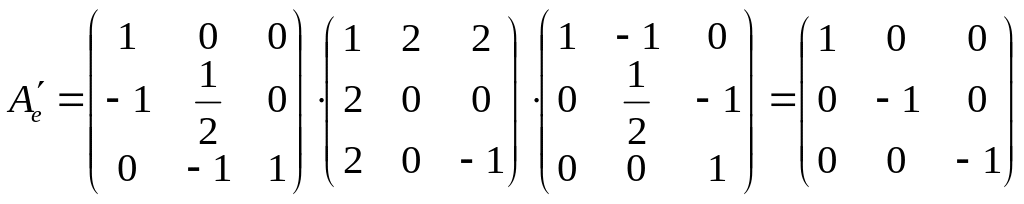Приклад 5. Задану квадратичну форму: звести до канонічного вигляду методом Лагранжа.

Виділимо повні квадрати, тоді матимемо:

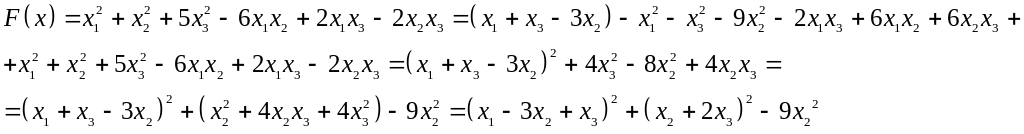
Після цього набуде канонічного вигляду:

, де .

.

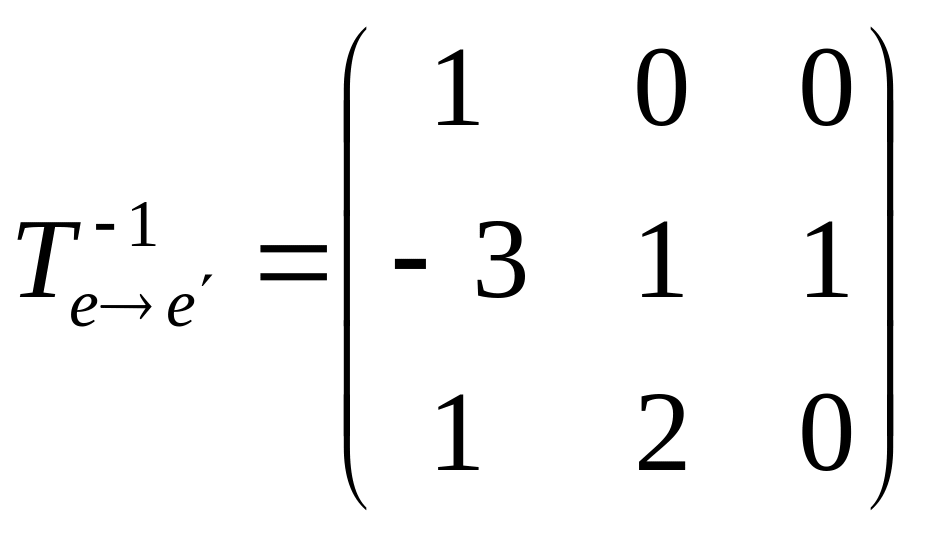Матриця перетворення: .

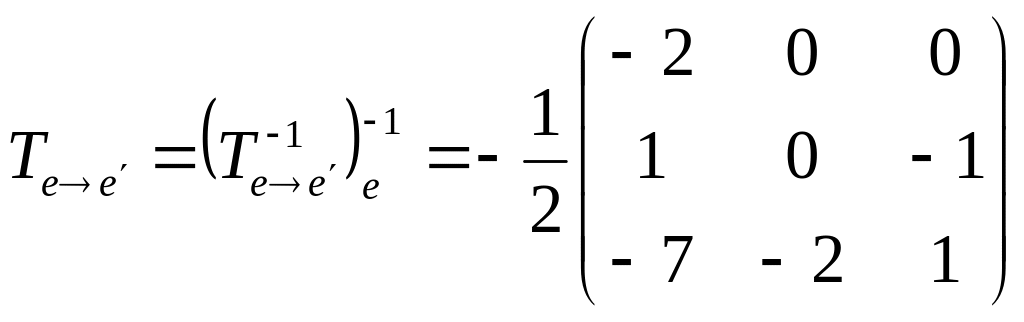Останні формули задають невироджене лінійне перетворення координат вектора в при переході до нового базису, в якому квадратична форма має канонічний вигляд: , а її матриця .

Перевірка.

І спосіб:

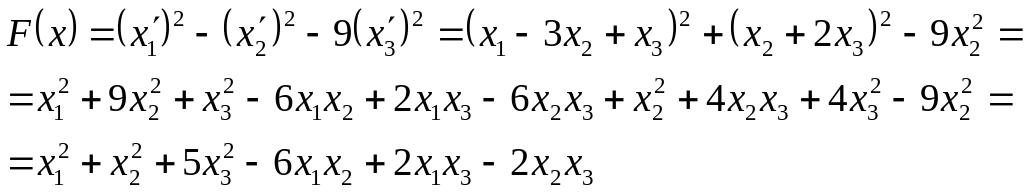
ІІ спосіб.

Здійснимо перевірку за формулою , де

- матриця квадратичної формули в базисі ;

- матриця переходу від базису до базису ;

- матриця квадратичної форми в базисі ;

- транспонована матриця переходу.

, .

;

.
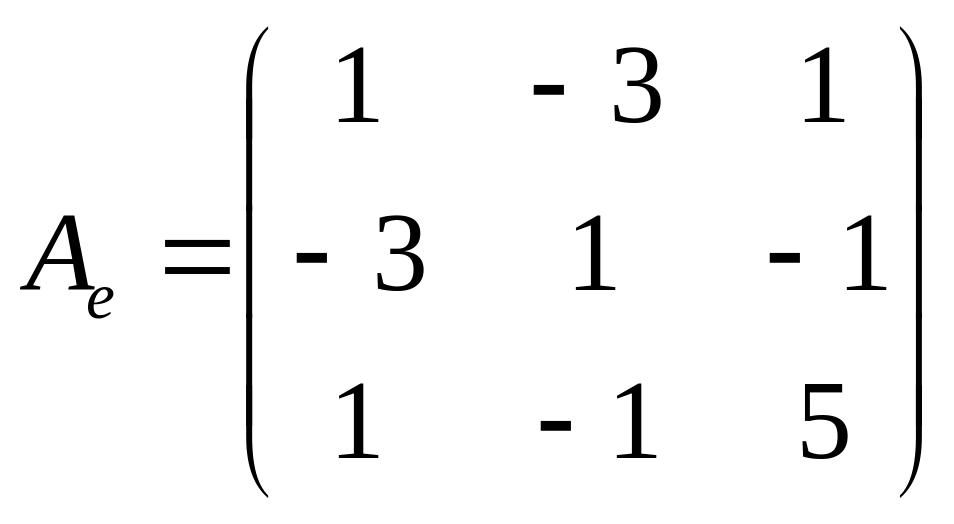
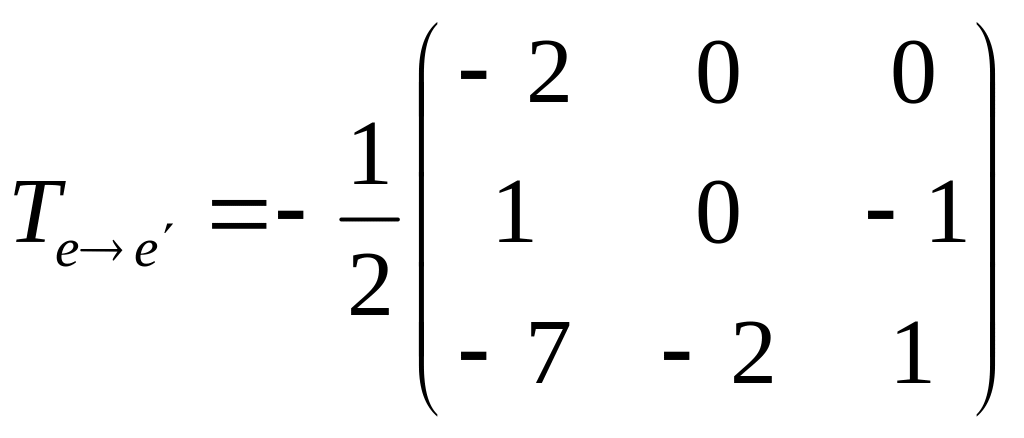
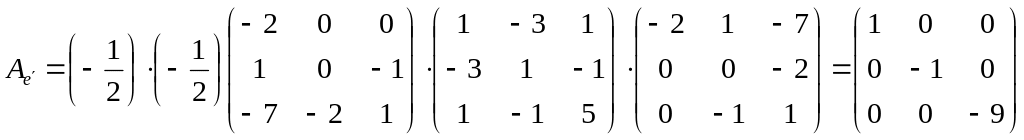