#14 Арифм. Действия с производными

 

а) 

б) 

Док-во: 1)Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).

Тогда

Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.

Следовательно,

.

2)Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому

Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).

Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.

Поэтому можем записать

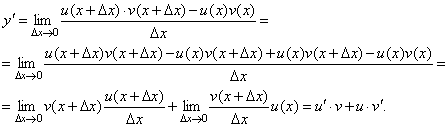
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.

3)Пусть  . Тогда

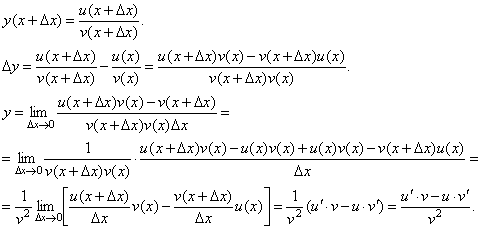
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.

#15 Таблица производных

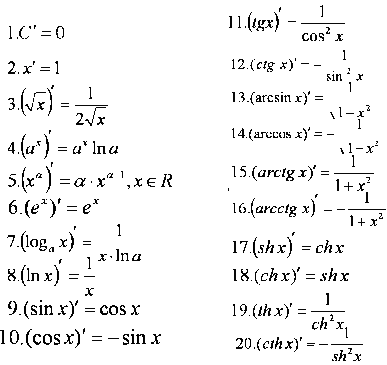
#16 Т.о производной сложной функции: пусть y=f(u(x))-сложная функция и пусть u(x) – диф. в т.x, а f(u) – диф в т.u тогда:

y=f(u(x)) – так же диф в т.x а ее производная вычисляется по формуле: y'=f(x)*u'(x)

Док-во: При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:

Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).

Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0, Δy→0.

По условию  . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0) , где α→0 при Δu→0, а, следовательно, и при Δx→0.

Перепишем это равенство в виде:

Δy= y'_uΔu+α·Δu.

Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx

.

По условию  . Поэтому, переходя к пределу при Δx→0, получим y '_x= y '_u·u '_x.

Т. о производной обратной функции:

Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(y0), отличную от нуля, то в соответствующей точке x0=g(y0) функция y=f(x) имеет производную f '(x0), равную  , т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.

Покажем, что  .

Пусть  . Тогда по свойству предела  . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е.  . Следовательно,

#17  Функция f(x) называется дифференцируемой в точке x, если ее приращение можно представить в виде y=A*x+o(x)*x, где A=const, lim(x0)(o(x))=0;

Линейная часть приращения функции, т.е. A*x  называется дифференциалом функции f(x) и обозначается df(x)=f(x)dx

Теорема(критерий): Чтобы ф-ия была диффер., необходимо, чтобы она имела в этой точке конечную производную.

Док-во: 1)Если y=f(x) - диффер., y=A*x+o(x)*x, y'=lim(x0)( y/x)=А;

2) lim(x00)(f(x))=f(x0),то o(x)= y/x-f'(x), принадлежит б/м ф-ии и o(x) 0, если x0, следовательно y=f'(x)*x+o(x)*x ;

Геометрический смысл: приращение

ординаты касательной. Dy=f’(x₀)dx; f’(x₀)=tg