7. Для розв’язання задачі № 7 використовуються формули з теми «Вибірка. Вибіркові числові характеристики»

Приклад

Дано результати вибірки, де спостерігалась випадкова величина . Побудувати ран жувальний ряд, інтервальний варіаційний ряд, розбивши діапазон значень ВВ на 5 інтервалів, полігон, гістограму, вибіркову функцію розподілу і її графік.

Знайти вибіркову середню, вибіркову дисперсію, вибіркове середнє квадратичне відхилення, виправлену дисперсію, виправлене середнє квадратичне відхилення, моду, медіану та розмах варіації.

41, 40, 32,35,39, 39,31,33, 37,36,41, 40,34,33, 32,37,38, 39,40,41, 35,36,34, 34,33

Розв’язання

Побудуємо ранжувальний ряд (записуємо варіанти у порядку зростання):

31, 32, 32, 33,33,33, 34,34,34, 35,35, 36,36, 37,37, 38, 39,39,39, 40,40,40, 41,41,41

Знайдемо довжину інтервалу за формулою

Побудуємо інтервальний варіаційний ряд

	(31;33)	(33;35)	(35;37)	(37;39)	(39;41)
	32	34	36	38	40
	3	6	4	3	9

Знайдемо вибіркову функцію розподілу, використовуючи формулу . Отже,

Знайдемо вибіркові числові характеристики:

	(31;33)	(33;35)	(35;37)	(37;39)	(39;41)
	32	34	36	38	40
	3	6	4	3	9

– вибіркова середня

– вибіркова дисперсія

– вибіркове середнє квадратичне відхилення

– виправлена дисперсія

,

– мода

, , ,

– медіана.

Вибірковою медіаною називається значення ВВ, яке приходиться на середину ранжувального ряду. Якщо проведено непарне число вимірювань n = 2q - 1 , тобто х₁, х₂, х_q-1, х_q, х_n, то . Якщо проведено парне число вимірювань n = 2q, то на середину ранжувального ряду приходиться два значення, тоді : .

– розмах варіації

Зауваження. Розглянемо приклад побудови графіка .

Приклад. Побудувати графік :

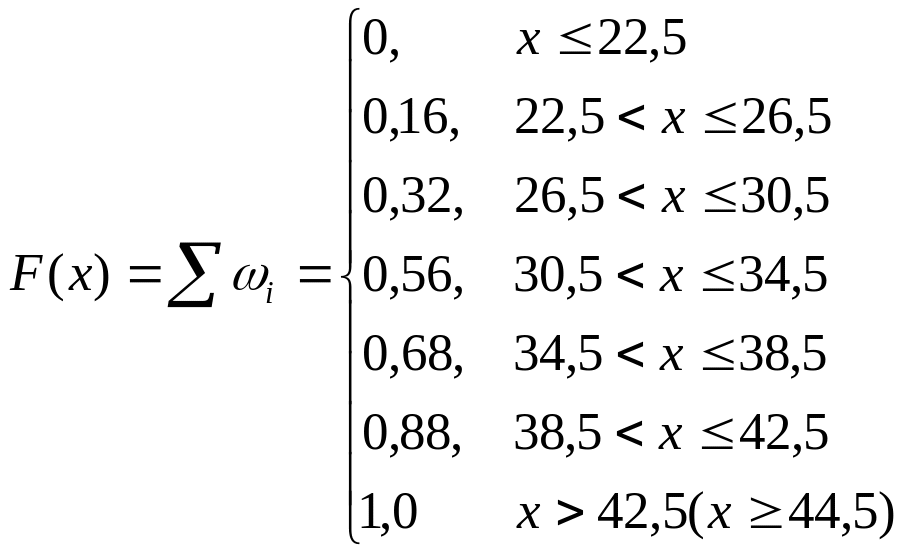
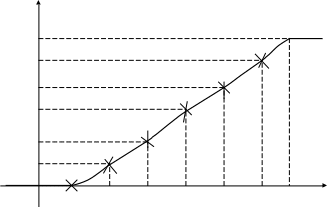
1,0

0,88

0,68

0,56

0,32

0,16

0 22,5 26,5 30,5 34,5 38,5 42,5 44,5 х

8. Для розв’язання задачі № 8 використовуються формули з теми «Інтервальні оцінки параметрів розподілу. Довірчі інтервали для математичного сподівання і дисперсії нормального розподілу».

Приклад

Проведено точних вимірів деякої фізичної величини і знайдено середнє арифметичне результатів вимірів . Всі виміри виконані одним приладом з відомим середнім квадратичним відхиленням похибок вимірів. Вважаючи результати вимірів нормально розподіленою величиною, знайти з надійністю довірливий інтервал для оцінки значення фізичної величини, яка вимірюється.

,

Розв’язання

Довірчий інтервал має вигляд

.

Значення знайдемо з умови , тобто , тоді за таблицею значень функції знайдемо .

Тоді, , ,

Таким чином,