Визначення знаків тригонометричних функцій у різних чвертях одиничного кола

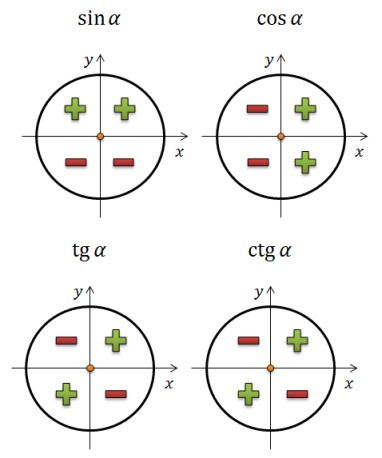
Додаток Б

Формули скороченого множення

1. (a + b)² = a² + 2ab + b²

2. (a – b) ² = a² – 2ab + b²

3. (a + b)³ = a³ + 3a²b + 3ab² + b³

4. (a – b)³ = a³ – 3a²b + 3ab² – b³

5. a² – b ² = (a – b)(a + b)

6. a³ – b ³ = (a – b)(a² + ab + b²)

7. a³ + b ³ = (a + b)(a² – ab + b²)

Додаток В

Найуживаніші тригонометричні формули

Розділимо всі тригонометричні формули на підгрупи, щоб легше орієнтуватися в них.

1.Основні тригонометричні тотожності:

sin² α + cos² α = 1 (1)

sin² α = 1 – cos² α

cos² α = 1 – sin² α ;

tg α = (2);

ctg α = (3);

tg α · ctg α = 1 (4);

1 + tg² α = (5),

1 + ctg α = (6);

2. Формули суми (різниці) функцій:

cos α + cos β = 2 cos cos (8);

cos α – cos β = – 2 sin sin (9);

tg α ± tg β = (10);

ctg α ± ctg β = (11);

3. Формули для суми (різниці) аргументів:

sin (α ± β ) = sin α · cos β ±cos α · sin β (12);

cos (α ± β ) = cos α · cos β sin α · sin β (13);

tg (α ± β )= (14);

4. Формули подвійного кута:

sin 2α = 2 sin α · cos α (15);

cos 2 α= cos² α – sin² α = 2 cos² α – 1 = 1– 2 sin² α (16);

tg 2α = (17);

ctg 2α = (18);

5. Формули половинного кута:

(19);

(20);

(21);

(22);

6. Формули перетворення добутків функцій:

sin α · sin β = (23);

sin α · cos β = (24);

cos α · cos β = (25);

7. Властивості парності (непарності)

sin (– α) = – sin α

cos (–α) = cos α

tg (–α) = – tg α

ctg (–α) = – ctg α (26);

8. Формули зведення:

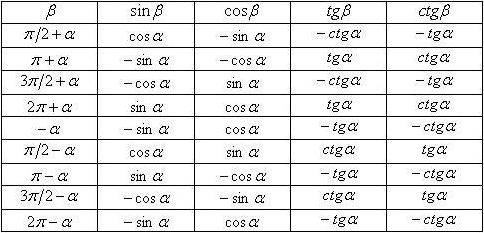
(27).

26