- •43. Pаспpеделение ошибок в дискpетных каналах связи.
- •44. Понятие блочных pазделимых и неpазделимых кодов. Паpаметpы коppектиpующих кодов.
- •45. Простейшие корректирующие коды. Двоичный код с контролем на четность. Код с постоянным весом. Оценка помехоустойчивости.
- •46. Простейшие корректирующие коды. Инверсный код. Корреляционный код. Оценка помехоустойчивости.
- •48. Групповой код. Проверочная матрица, синдром ошибки. Условия обнаружения и исправления ошибок. Таблица декодирования.
- •49. Код Хемминга.
- •50. Циклический код. Основные сведения. Построение циклического кода.
- •51. Циклический код. Основные сведения. Способы описания (образующая и пpовеpочная матpицы).
- •52. Циклический код. Обнаpужение и испpавление ошибок. Оценка помехоустойчивости.
- •53. Циклический код. Способы кодирования и декодирования. Структурная реализация кодирующих и декодирующих устройств.
- •54. Синтез аналоговых фильтров нижних частот.(нет ответа)
- •55. Понятие многомерных дискретных сигналов. Многомерное преобразование Фурье. Понятие двумерного дискретного преобразования Фурье.
- •56. Понятие многомерных дискретных систем. Динамические характеристики и связь между ними. Определение выходной последовательности. Понятие многомерной свертки.
48. Групповой код. Проверочная матрица, синдром ошибки. Условия обнаружения и исправления ошибок. Таблица декодирования.
Вторым способом задания группового кода является проверочная матрица
где Ik − единичная квадратная матрица ранга k, построенная на позициях контрольных символов;
транспонированная матрица контрольных символов, построенная на позициях информационных символов. Проверочная матрица дает связь между информационными и контрольными символами. На этой основе можно построить кодер. Кроме того, она используется для обнаружения и исправления ошибок. Ошибочная комбинация группового кода может быть представлена как где β – безошибочная комбинация; l − двоичная последовательность (комбинация ошибки) длины n, содержащая единицы только в тех разрядах, которые искажены. При отсутствии ошибок имеем
Двоичная последовательность D= d1d2… dk называется синдромом (опознавателем) ошибки. Если синдром состоит из одних нулей, комбинация считается безошибочной. Ненулевая величина синдрома говорит о наличии ошибки. Число ненулевых синдромов равно 2 в степени k −1. Ошибку l можно исправить, если ей соответствует индивидуальный синдром. Если разным ошибкам отвечает один и тот же синдром, то они не различаются и их можно только обнаружить. Вместо (2.1) и (2.2) набор синдромов удобно получать непосредственно из проверочной матрицы. В матрице Hk,n i-й столбец представляет собой синдром одиночной ошибки в i-м разряде кодовой комбинации. Остальные синдромы находят поразрядным суммированием по модулю 2 столбцов проверочной матрицы в различных сочетаниях. Если код исправляет ошибки, то полученные синдромы сводятся в таблицу декодирования. В ней приводятся комбинация ошибки l, вид синдрома D и действие декодирующего устройства: выдача принятой комбинации получателю при нулевом синдроме, стирание принятой комбинации при обнаружении факта наличия неисправляемых кодом ошибок, исправление i-го разряда в принятой комбинации при получении синдрома, соответствующего ошибке в i-ом разряде. Поскольку получателю выдаются только информационные разряды, исправление ошибок в контрольных разрядах обычно не производится.
Пример 2. Составим проверочную матрицу и набор синдромов для груп-пового кода (2,4) из примера 1. Матрица контрольных символов
В данном примере двум разным одиночным ошибкам соответствует оди-наковый синдром D=10. Поэтому код (2,4) не обеспечивает исправление одиночной ошибки. Так как двойной ошибке l = l1l2l3l4 → 0110 отвечает нулевой синдром D=00, то данный код не позволяет обнаруживать все двойные ошибки.
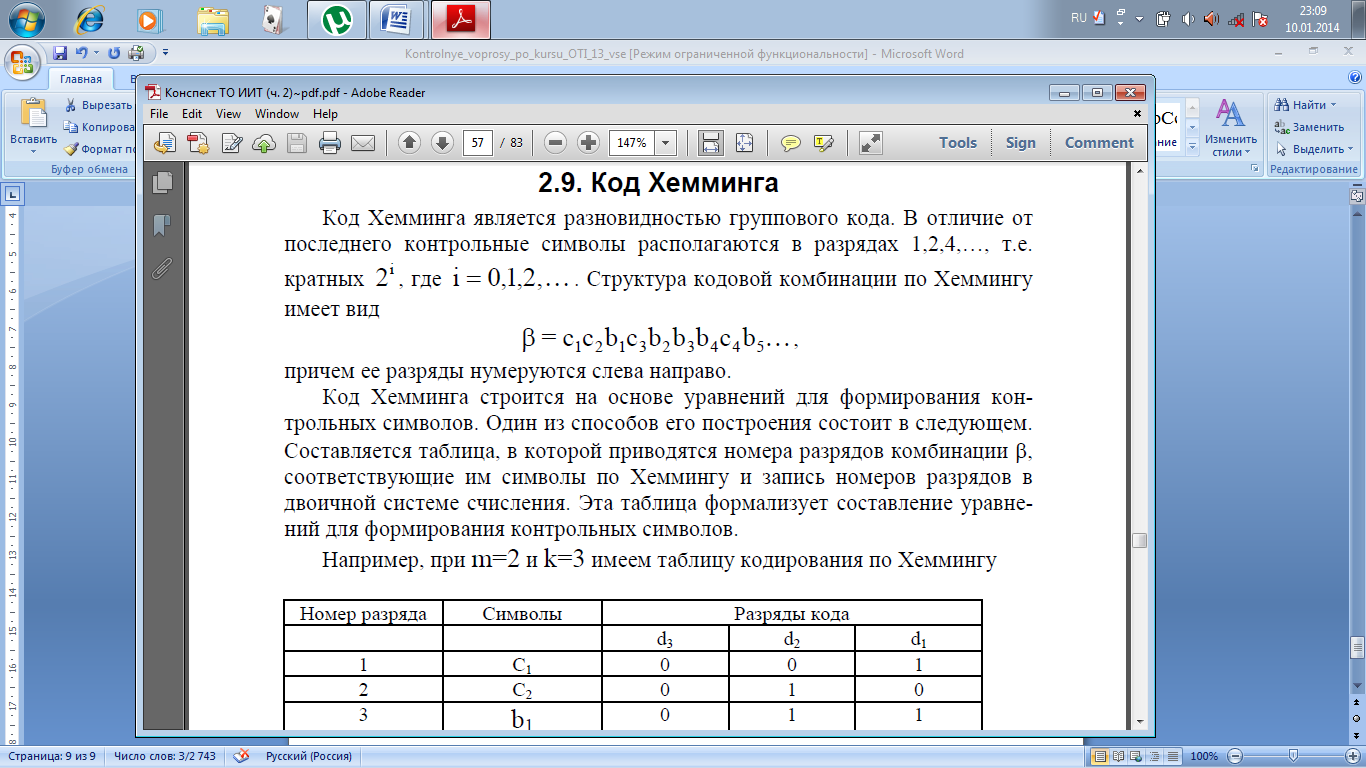
49. Код Хемминга.
 Код
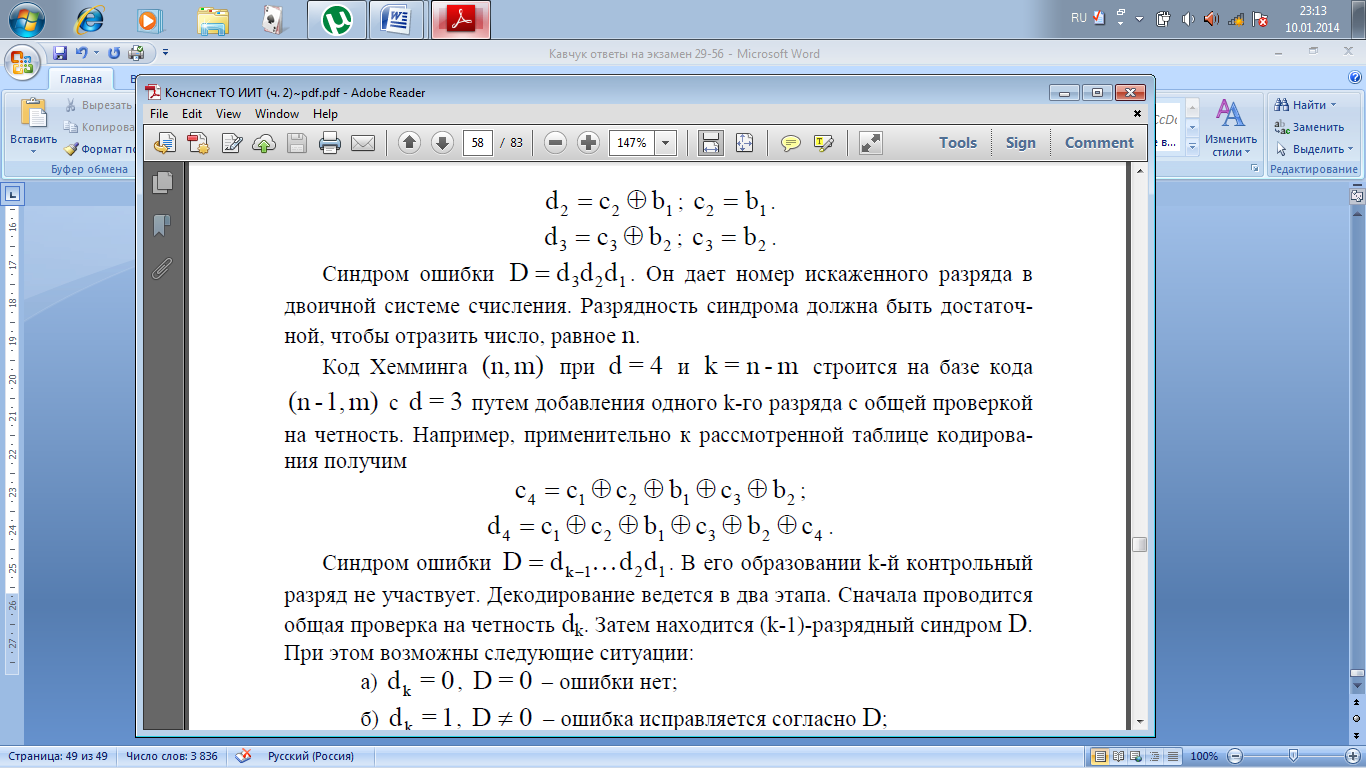
Хемминга строится на основе уравнений
для формирования кон-трольных символов.
Один из способов его построения состоит
в следующем.Составляется таблица, в
которой приводятся номера разрядов
комбинации β,соответствующие им символы
по Хеммингу и запись номеров разрядов
в двоичной системе счисления. Эта таблица
формализует составление уравнений для
формирования контрольных символов.Например,
при m=2 и k=3 имеем таблицу кодирования по
Хеммингу
Код
Хемминга строится на основе уравнений
для формирования кон-трольных символов.
Один из способов его построения состоит
в следующем.Составляется таблица, в
которой приводятся номера разрядов
комбинации β,соответствующие им символы
по Хеммингу и запись номеров разрядов
в двоичной системе счисления. Эта таблица
формализует составление уравнений для
формирования контрольных символов.Например,
при m=2 и k=3 имеем таблицу кодирования по
Хеммингу

 Код
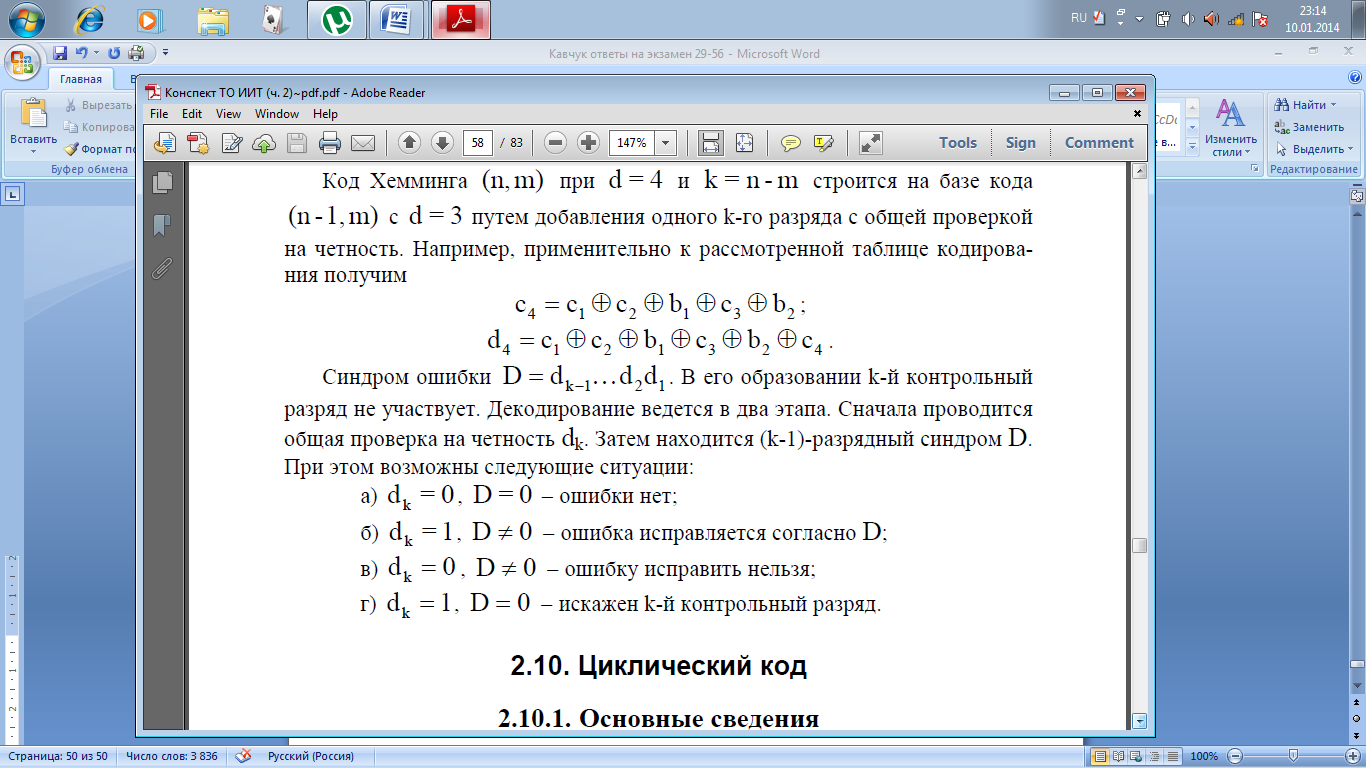
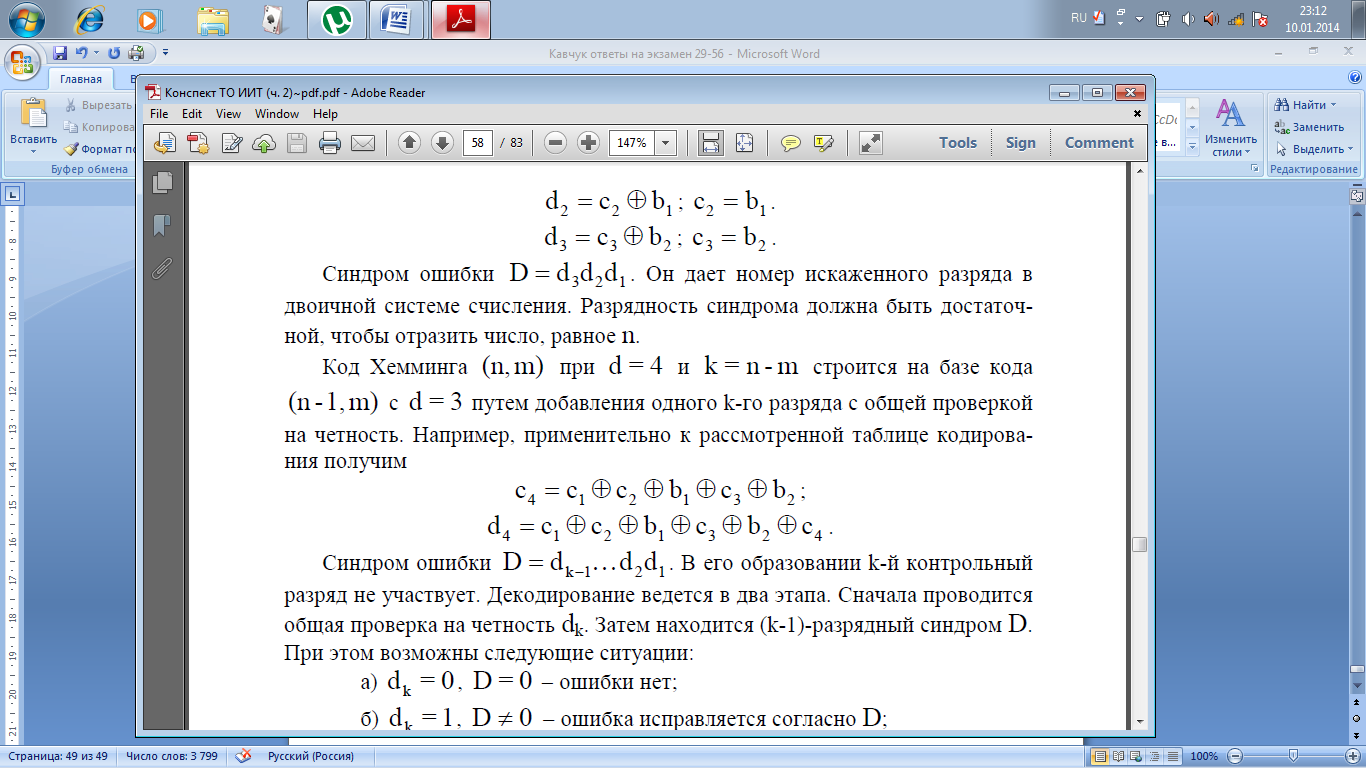
Хемминга (n,m) при d = 4 и k = n-m строится на
базе кода(n -1,m) с d = 3 путем добавления
одного k-го разряда с общей проверкой
на
четность. Например, применительно к
рассмотренной таблице кодирования
получим
Код
Хемминга (n,m) при d = 4 и k = n-m строится на
базе кода(n -1,m) с d = 3 путем добавления
одного k-го разряда с общей проверкой
на
четность. Например, применительно к
рассмотренной таблице кодирования
получим