- •43. Pаспpеделение ошибок в дискpетных каналах связи.
- •44. Понятие блочных pазделимых и неpазделимых кодов. Паpаметpы коppектиpующих кодов.
- •45. Простейшие корректирующие коды. Двоичный код с контролем на четность. Код с постоянным весом. Оценка помехоустойчивости.
- •46. Простейшие корректирующие коды. Инверсный код. Корреляционный код. Оценка помехоустойчивости.
- •48. Групповой код. Проверочная матрица, синдром ошибки. Условия обнаружения и исправления ошибок. Таблица декодирования.
- •49. Код Хемминга.
- •50. Циклический код. Основные сведения. Построение циклического кода.
- •51. Циклический код. Основные сведения. Способы описания (образующая и пpовеpочная матpицы).
- •52. Циклический код. Обнаpужение и испpавление ошибок. Оценка помехоустойчивости.
- •53. Циклический код. Способы кодирования и декодирования. Структурная реализация кодирующих и декодирующих устройств.
- •54. Синтез аналоговых фильтров нижних частот.(нет ответа)
- •55. Понятие многомерных дискретных сигналов. Многомерное преобразование Фурье. Понятие двумерного дискретного преобразования Фурье.
- •56. Понятие многомерных дискретных систем. Динамические характеристики и связь между ними. Определение выходной последовательности. Понятие многомерной свертки.
43. Pаспpеделение ошибок в дискpетных каналах связи.
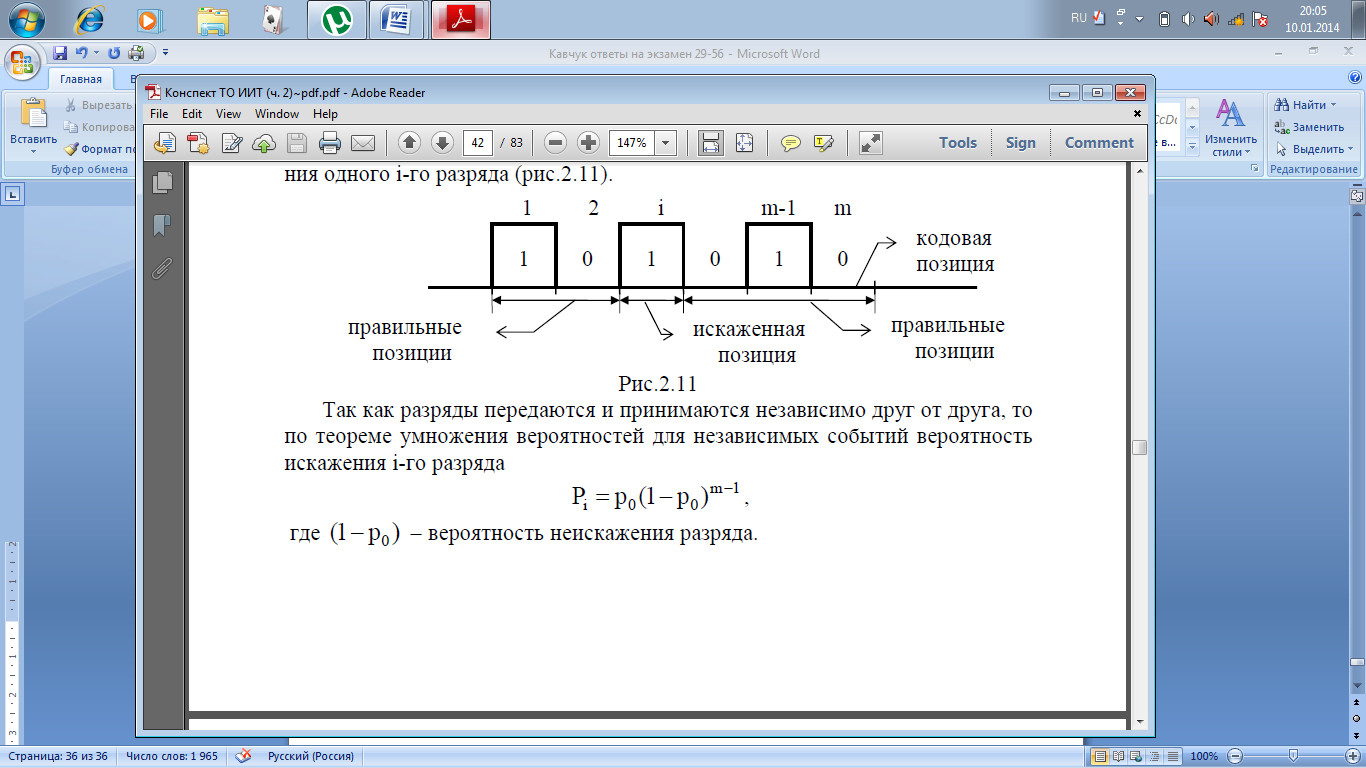
Пусть кодовая комбинация состоит из m независимых двоичных символов. Пусть она передается по двоичному симметричному каналу, который имеет вероятность ошибки p 0. Найдем вероятность P(1,m) того, что в m-разрядной кодовой комбинации будет ровно 1 ошибка. Предварительно определим вероятность искажения одного i-го разряда (рис.2.11).
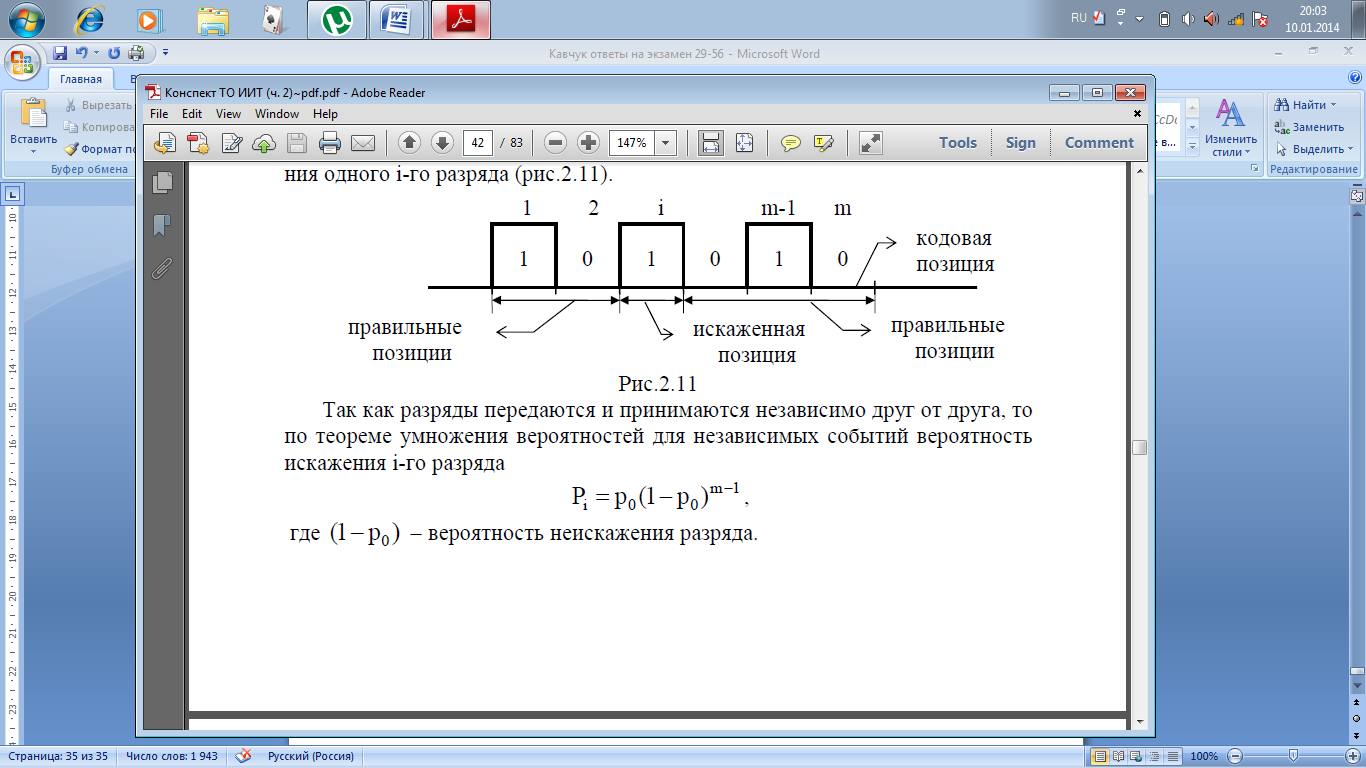
Так как разряды передаются и принимаются независимо друг от друга, то по теореме умножения вероятностей для независимых событий вероятность искажения i-го разряда
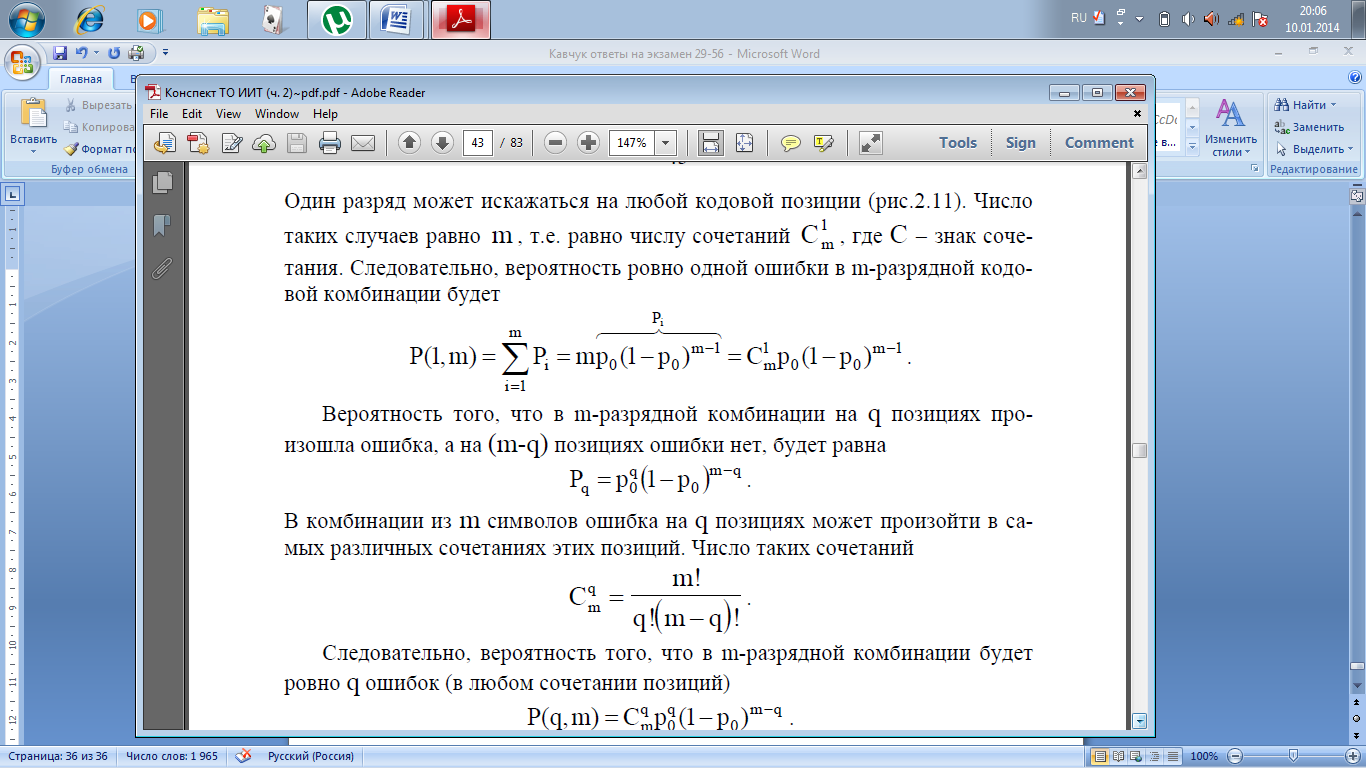
Вероятность
того, что в m-разрядной комбинации на q
позициях произошла ошибка, а на (m-q)
позициях ошибки нет, будет равна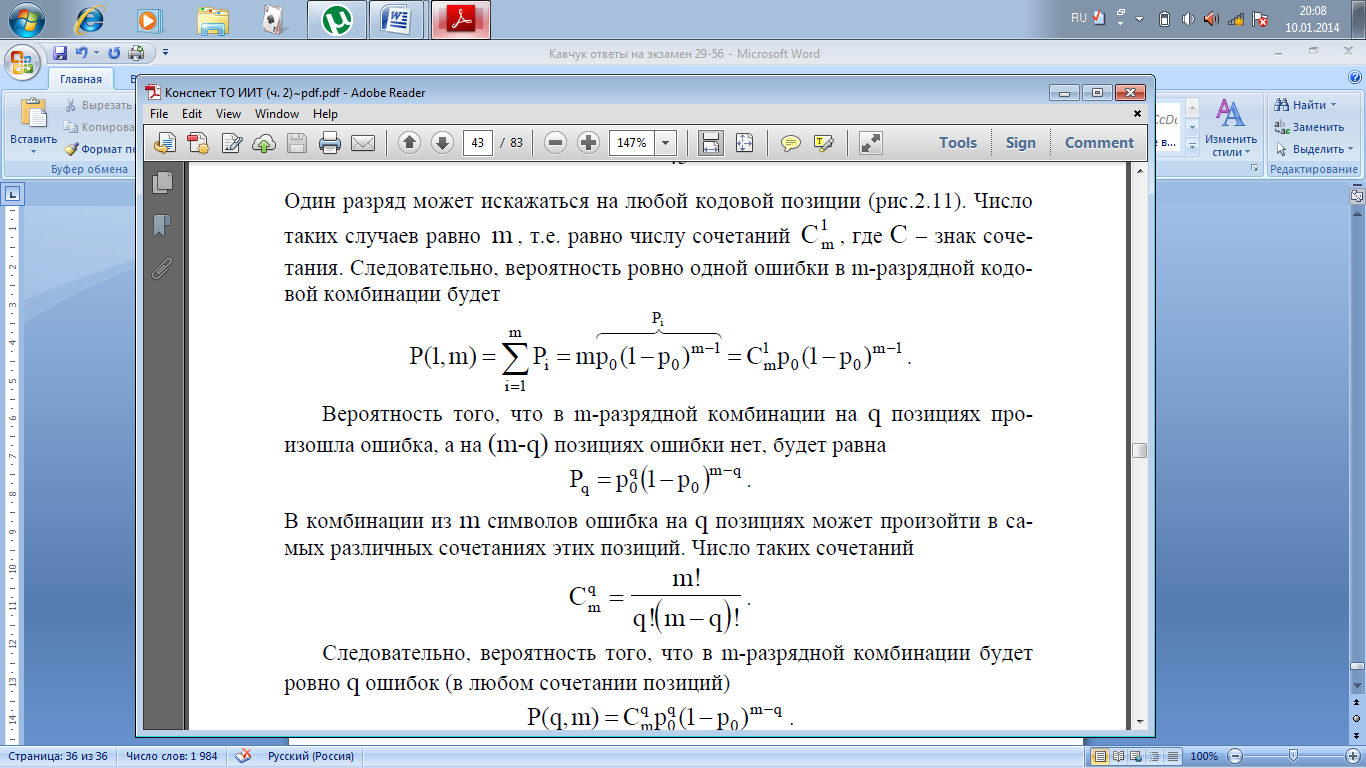
В комбинации из m символов ошибка на q позициях может произойти в самых различных сочетаниях этих позиций. Число таких сочетаний
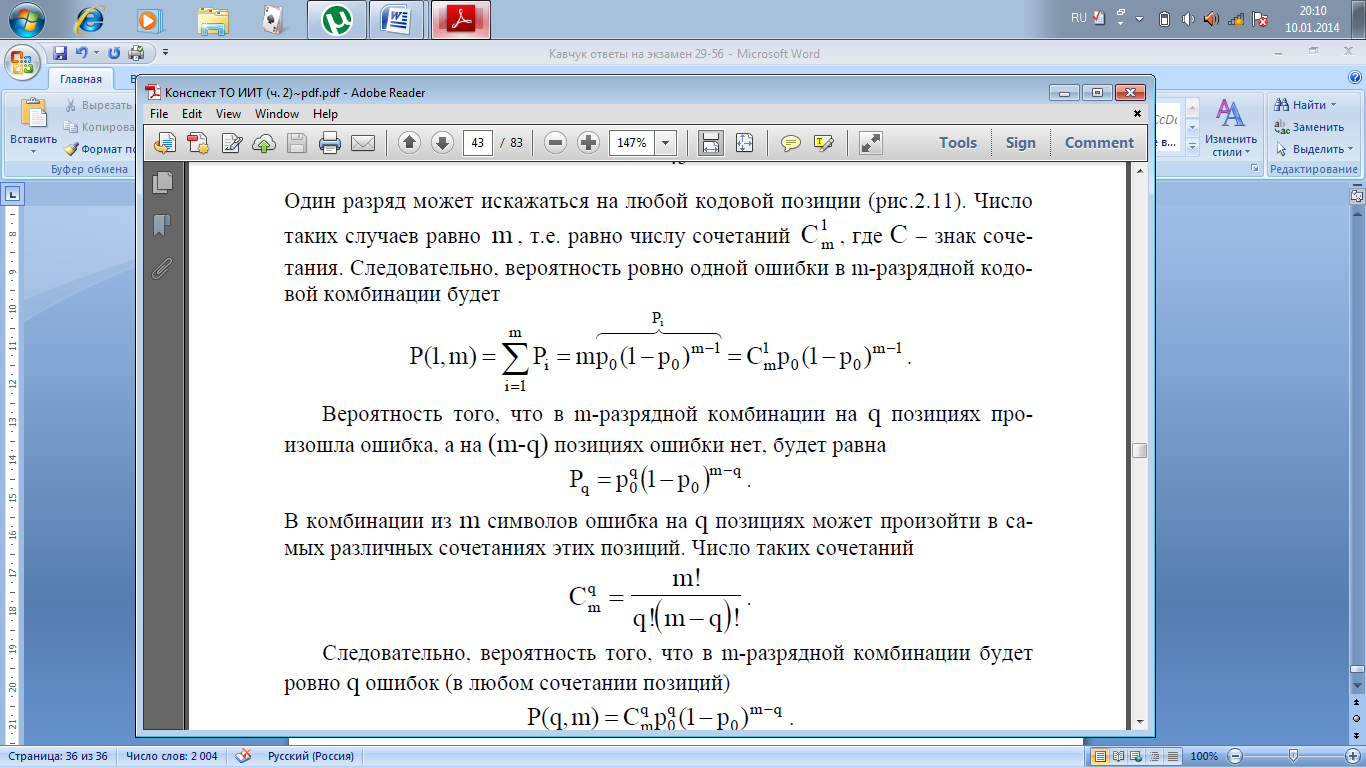 Следовательно,
вероятность того, что в m-разрядной
комбинации будет ровно q ошибок (в любом
сочетании позиций)
Следовательно,
вероятность того, что в m-разрядной
комбинации будет ровно q ошибок (в любом
сочетании позиций)
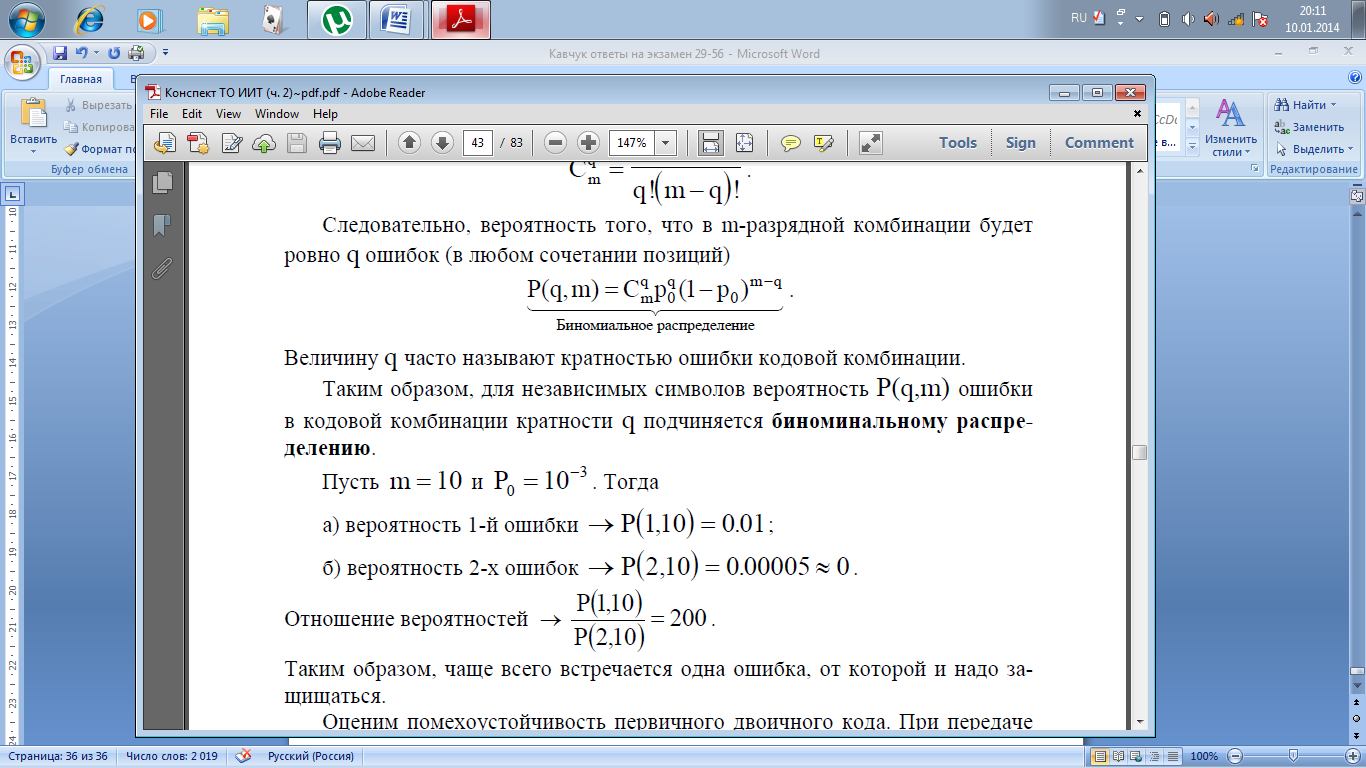 Величину
q часто называют кратностью ошибки
кодовой комбинации. Таким образом, для
независимых символов вероятность P(q,m)
ошибки в кодовой комбинации кратности
q подчиняется биноминальному
распределению.
Величину
q часто называют кратностью ошибки
кодовой комбинации. Таким образом, для
независимых символов вероятность P(q,m)
ошибки в кодовой комбинации кратности
q подчиняется биноминальному
распределению.
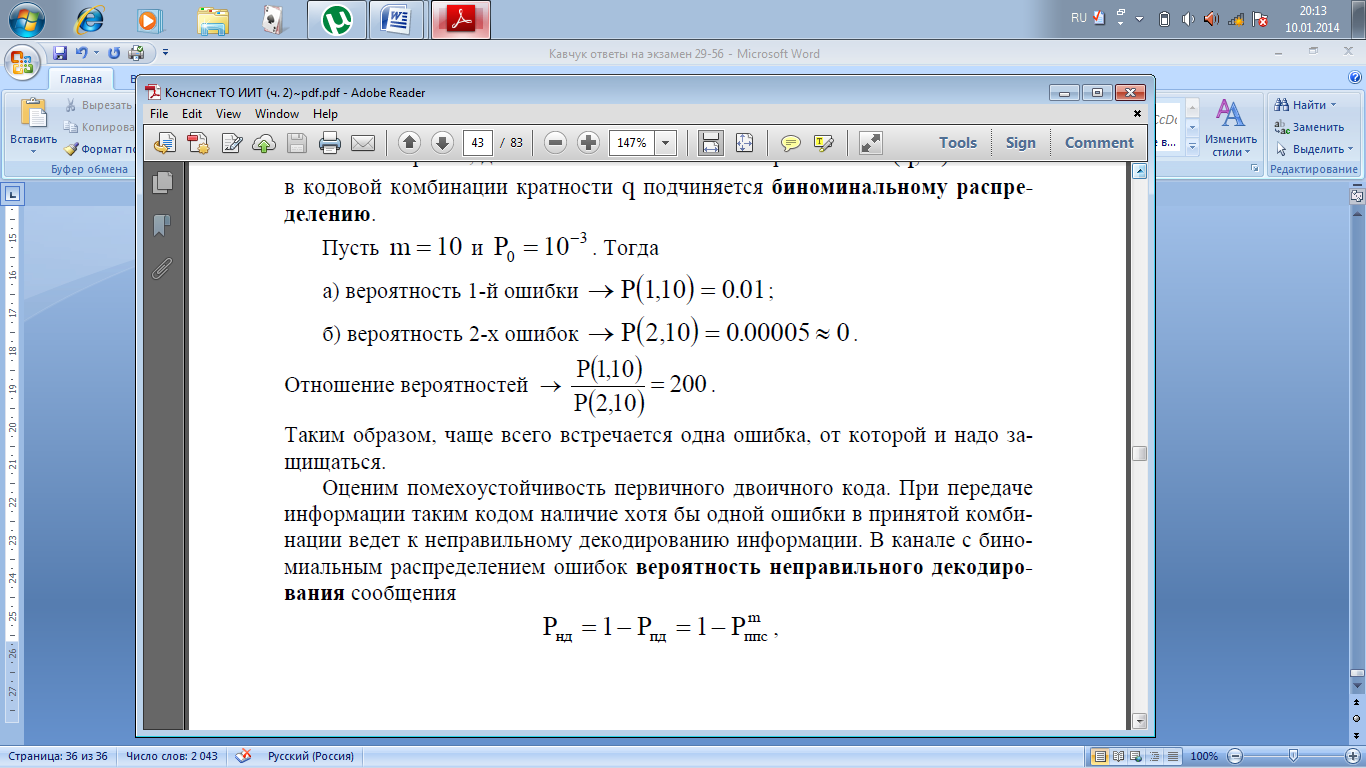
Таким
образом, чаще всего встречается одна
ошибка, от которой и надо за-щищаться.
Оценим помехоустойчивость первичного
двоичного кода. При передаче информации
таким кодом наличие хотя бы одной ошибки
в комби-нации ведет к неправильному
декодированию информации. В канале с
бино-миальным распределением ошибок
вероятность
неправильного декодиро-вания сообщения![]()
44. Понятие блочных pазделимых и неpазделимых кодов. Паpаметpы коppектиpующих кодов.
Различают разделимые и неразделимые блочные коды. В разделимых кодах позиции информационных и контрольных символов раздельны. Обычно эти коды условно обозначают в виде (n,m) , где n − общая длина кодовой комбинации, m − число информационных символов. Тогда число проверочных символов k = n-m. В неразделимых кодах информационные и контрольные символы разделить нельзя. Основные параметры, характеризующие корректирующие свойства: 1) избыточность кода − R; 2) кодовое расстояние − d; 3) число обнаруживаемых кодом ошибок − r; 4) число исправляемых кодом ошибок − S. Избыточностью кода называют величину
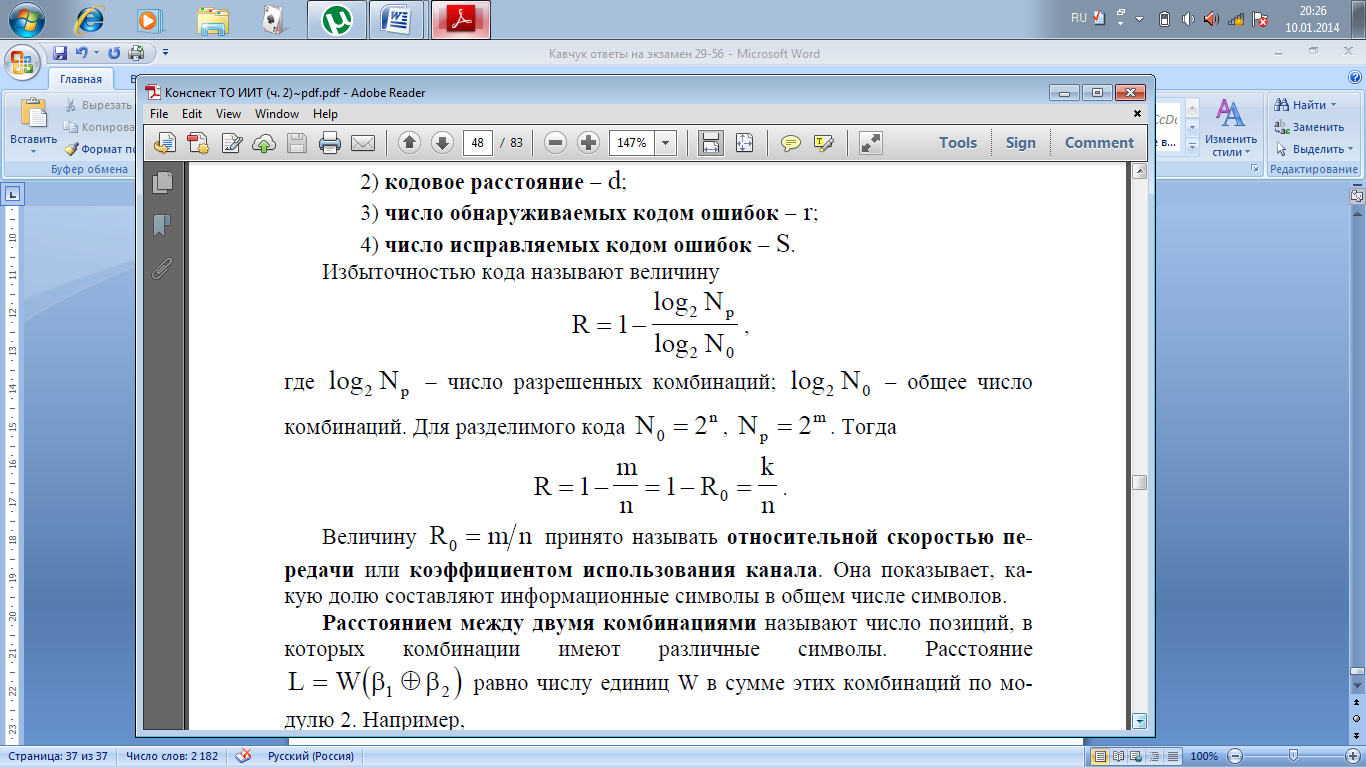
Величину R0= m/n принято называть относительной скоростью передачи или коэффициентом использования канала. Она показывает, какую долю составляют информационные символы в общем числе символов. Расстоянием между двумя комбинациями называют число позиций, в которых комбинации имеют различные символы .Расстояние L = W(β1 ⊕β2 ) равно числу единиц W в сумме этих комбинаций по модулю 2. Например,
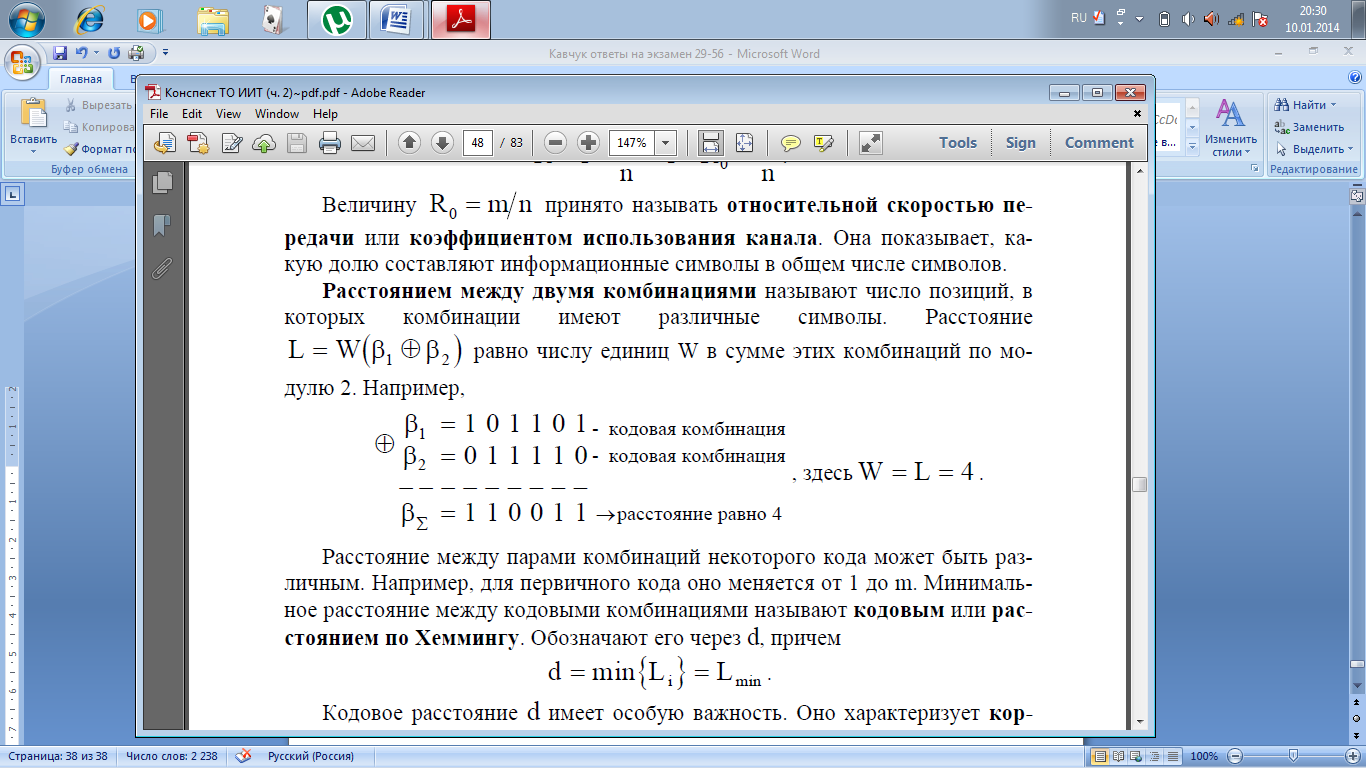
Расстояние между парами комбинаций некоторого кода может быть раз-личным. Например, для первичного кода оно меняется от 1 до m. Минималь-ное расстояние между кодовыми комбинациями называют кодовым или рас-стоянием по Хеммингу. Обозначают его через d, причем
![]() Кодовое
расстояние d имеет особую важность. Оно
характеризует корректирующие свойства
кода. Для обнаружения ошибок кратности
r и менее необходимо и достаточно, чтобы
кодовое расстояние было равно d ≥ r +1.
Кратность ошибки − это число
искаженных позиций кодовой комбинации.
Для исправления ошибок кратности S и
менее необходимо иметь d ≥ 2S +1. Для
исправления ошибок кратности S и
одновременного обнаружения ошибок
кратности r >S нужно иметь d
≥ r
+S
+1( r
≥ S
), при r
= S→d
≥ 2S
+1. Связь между кодовым расстоянием и
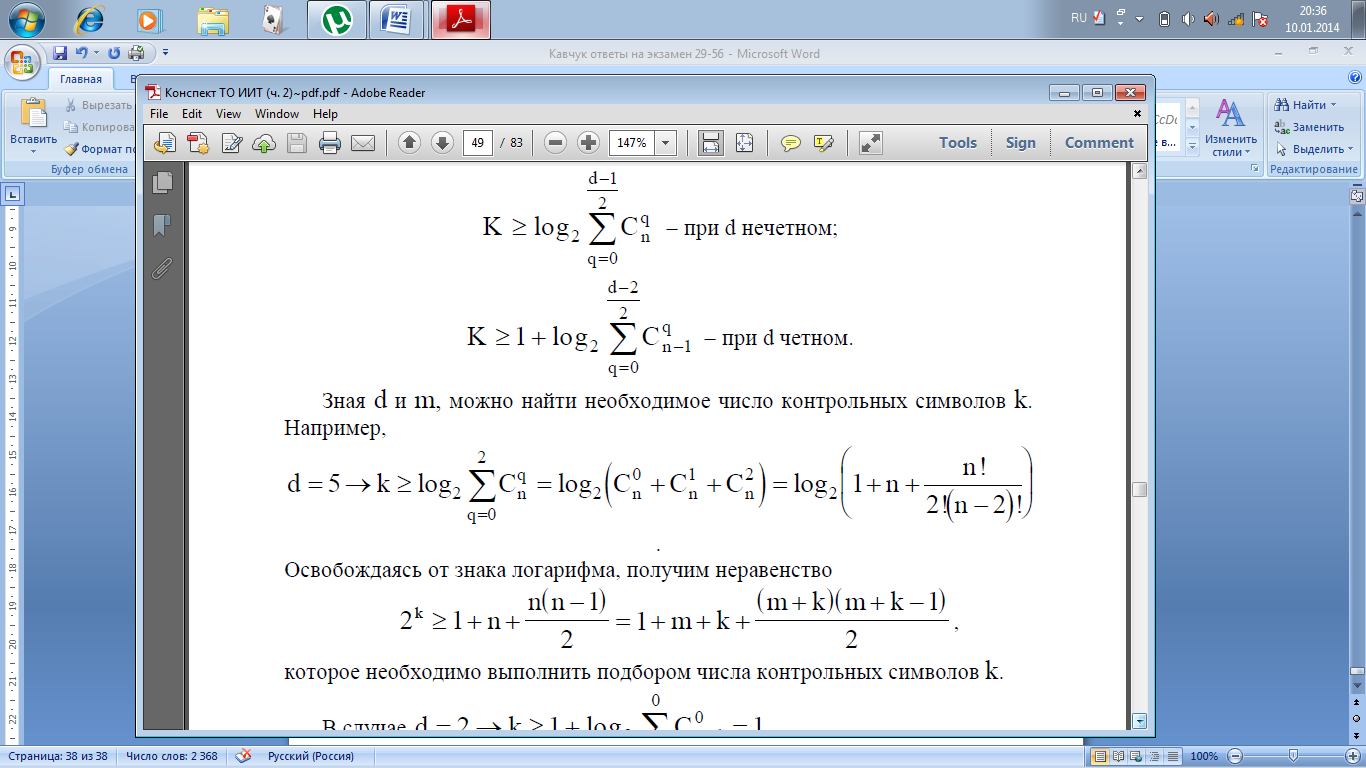
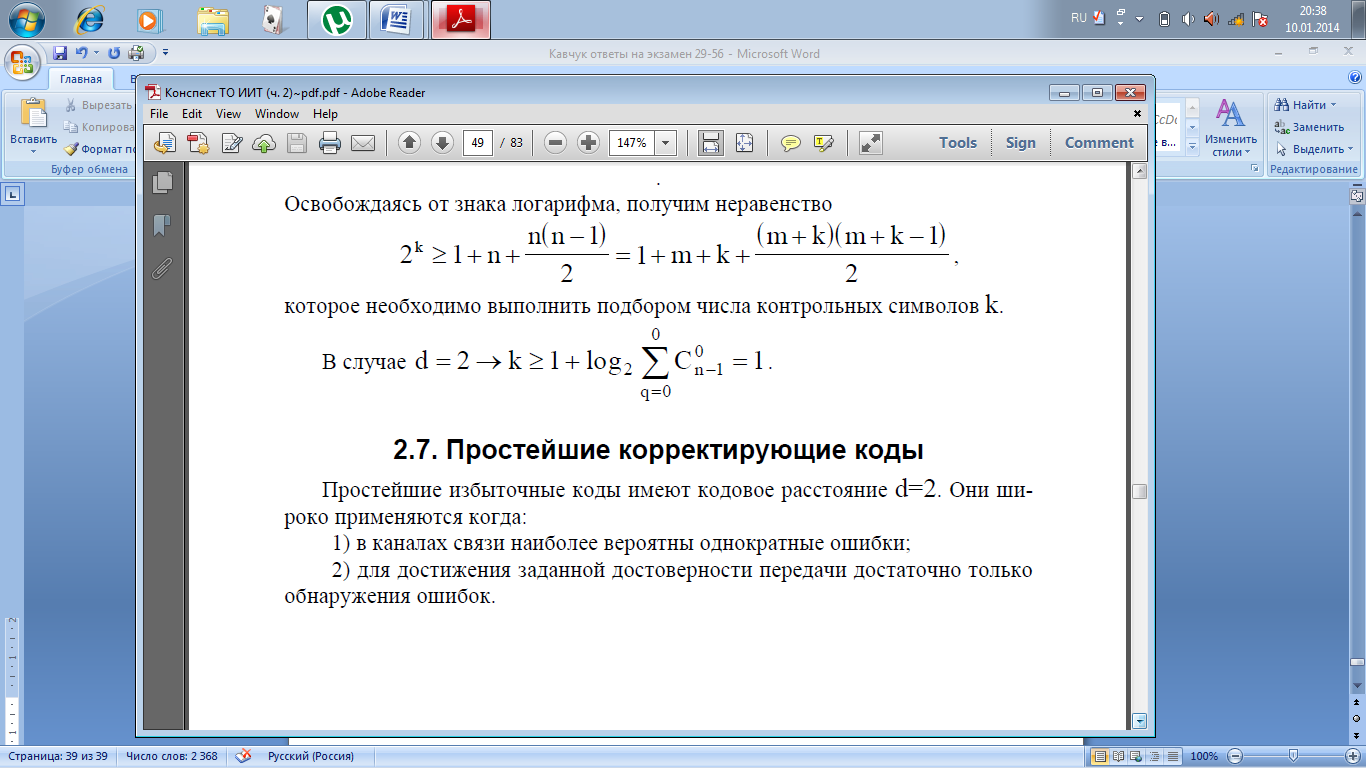
числом контрольных символов ус-танавливается
с помощью оценок Хемминга
Кодовое
расстояние d имеет особую важность. Оно
характеризует корректирующие свойства
кода. Для обнаружения ошибок кратности
r и менее необходимо и достаточно, чтобы
кодовое расстояние было равно d ≥ r +1.
Кратность ошибки − это число
искаженных позиций кодовой комбинации.
Для исправления ошибок кратности S и
менее необходимо иметь d ≥ 2S +1. Для
исправления ошибок кратности S и
одновременного обнаружения ошибок
кратности r >S нужно иметь d
≥ r
+S
+1( r
≥ S
), при r
= S→d
≥ 2S
+1. Связь между кодовым расстоянием и
числом контрольных символов ус-танавливается
с помощью оценок Хемминга