51. Напряжения в поперечных сечениях стержня при чистом изгибе.

      Рассмотрим наиболее простой случай изгиба, называемый чис­тым изгибом. Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а попе­речные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, согласно второго выражения (5.4), вдоль продольной оси zпринимает постоянное значение. Так как в любом сечении стержня при чистом изгибеMx(z) = const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих мо­ментов ось бруса искривляется. Исходя из этого, ось бруса прини­мает форму дуги окружности с радиусом кривизны  (рис. 5.6). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба пере­местятся в пространстве таким образом, что их совокупность снова образует плоскость.

      Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сече­ний друг относительно друга.

      Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии dz(рис. 5.6).

      В результате изгиба эти сечения наклонятся, образуя между со­бой угол d , в связи с чем верхние волокна удлиняются, а ниж­ние  укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом CD = CD= dz = d. Произвольный отрезок АВ, расположен­ный от СD на расстоянии y, в результате изгиба удлинится на величинуA B   AB. С учетом построений, изображенных на рис. 5.6, легко определить величину его линейной деформации:

.   (5.6)

      Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения  сжатия. Тогда переход от деформаций к нормальным напряжениям  можно осуществить посредством закона Гука:

                                                                                          (5.7)

52. Касательные напряжения. Формула Жуковского.

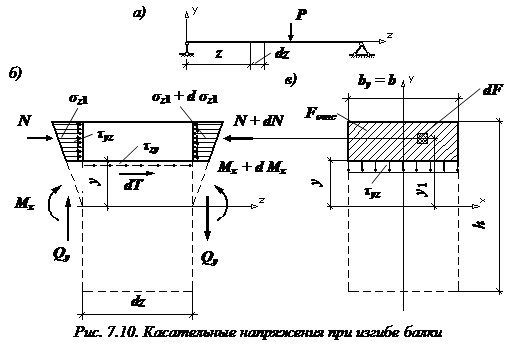
Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.

Вырежем из балки прямоугольного поперечного сечения (рис. 7.10, а) элемент длиной  и дополнительным продольным сечением рассечем на две части (рис. 7.10, б).

Рассмотрим равновесие верхней части: из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Чтобы эта часть балки находилась в равновесии ( ) в ее продольном сечении должна возникнуть касательная сила  . Уравнение равновесия части балки:

Отсюда

,

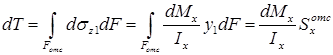где интегрирование ведется только по отсеченной части площади поперечного сечения балки  (на рис. 7.10, в заштрихована),  – статический момент инерции отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.

Предположим: касательные напряжения ( ), возникающие в продольном сечении балки, равномерно распределены по ее ширине ( ) в месте сечения:

Получим выражение для касательных напряжений:

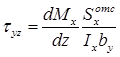
, а  , тогда формула касательных напряжений ( ), возникающих в точках поперечного сечения балки, находящихся на расстоянии yот нейтральной оси x:

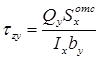- формула Журавского

Формула Журавского получена в 1855 г. Д.И. Журавским, поэтому носит его имя.

При поперечном изгибе в сечении балки помимо изгибающего момента ( )возникает поперечная сила ( ). Поэтому в поперечном сечении при поперечном изгибе наряду с нормальными напряжениями ( ) возникают и касательные напряжения ( ).

На основании закона парности касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибеотмечаются сдвиги продольных слоев балки относительно друг друга.

При поперечном изгибе гипотеза плоских сечений нарушается, поскольку поперечные сечения балки искривляются (рис. 7.9).

Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе:  .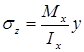

Проанализируем формулу Журавского:

Поперечная сила ( ) для конкретного сечения и момент инерции поперечного сечения относительно нейтральной оси  являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения ( ) к ширине поперечного сечения ( ), в котором они вычисляются.

Во всех точках поперечного сечения, расположенных на расстоянии y отнейтральной линии (по всей ширине сечения  ), касательные напряжения при поперечном изгибе одинаковы.

В самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения при поперечном изгибе равны 0, поскольку в этом случае  .

Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю

Формула Жуковского

 (4) где   ширина сечения на том уровне, где определяется напряжение  статический момент отсеченной (заштрихованной) части сечения относительно оси  .